| Titel: | Ueber Anwendung der Tangenten-Schrauben auf Theodolite etc. Von dem sel. Hrn. Jak. Allan, mathematischen Instrumenten-Macher zu London. |
| Fundstelle: | Band 18, Jahrgang 1825, Nr. XXVI., S. 141 |
| Download: | XML |
XXVI.
Ueber Anwendung der Tangenten-Schrauben auf
Theodolite etc. Von dem sel. Hrn. Jak.
Allan, mathematischen Instrumenten-Macher zu
London.
Aus den XXXIV. B. der Transaction of the Society for
Encouragement in Gill's technical Repository. Jun. 1825. S.
370.
Mit Abbildungen auf Tab.
III.
Allan, uͤber Anwendung der Tangenten-Schrauben.
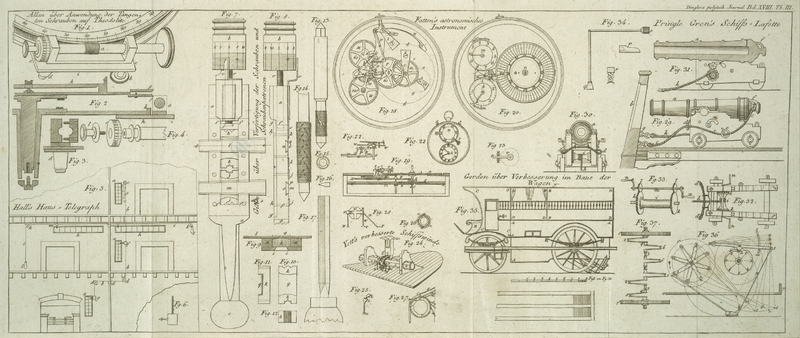
Fig. 1. stellt
einen Theil des Theodoliten, ungefaͤhr 8 Zoll im Durchmesser, vor,
eingetheilt in halbe Grade, und mit der Tangenten-Schraube, a, in genauer Beruͤhrung mit dem Umfange desselben. b, ist die Schraube, die sie befestigt, und durch deren
Nachlassen sie abgenommen werden kann; etc, das Schraubengestell, das sich frei auf
der Achse d, bewegt, um welche es sich dreht. Da der
Theodolit in halbe Grade getheilt ist, so ist der Rand in eben so viele
Zaͤhne (720) geschnitten, und folglich bewegt eine ganze Umdrehung den
Theodoliten um einen halben Grad. e, ist der Mikrometer
an dem Haupte der Schraube, a, welcher in 30 Theile
eingetheilt ist, die die Minuten geben, und da jeder derselben wieder in 4 Theile
getheilt ist, (also in Allem in 120 Theile), so gibt dieß Viertel-Minuten.
Fig. 2. ist
ein Durchschnitt eines Theiles des kreisfoͤrmigen Ringes, der Achse der
Magnetnadel, und des Theodoliten. Die Theile sind in einiger Entfernung von einander
dargestellt, um den Bau derselben desto deutlicher zu zeigen. Der zahnige Rand der
Scheibe ist in seiner Mitte getrennt oder gehaͤlftet: die obere
Haͤlfte, g, ist ein flacher Ring, der auf die
untere Haͤlfte, f, aufgeschraubt ist mittelst 12
Schrauben, wovon jede 30 Grade von der anderen entfernt steht. h, ist der Rand der unteren Platte des Theodoliten, auf
welcher der Kreis sich bewegt, und der Stiefel der Achse, die Schraube und der
Waͤscher, i, die Platte, welche das Gestelle der
Tangenten-Schraube fuͤhrt; a, der Durchschnitt
derselben, und k, die Magnetnadel in ihrem
Gehaͤuse.
Fig. 3. ist
ein Theil des Gestelles der Tangenten-Schraube mit der Zwinge und ihren beiden
Schrauben, um ein Ende oder den Hals der Achse der Tangenten-Schraube, der in Fig. 4.
dargestellt ist, festzuhalten, so wie auch die kurze Achse d, auf welcher das Gestell sich dreht.
Fig. 4. das
Ende der Achse der Tangenten-Schraube mit abgenommenem Mikrometer, l, die kleine Schraube, wodurch der aufgezogene
Mikrometer festgehalten wird.
Auf diesem Theodoliten werden die Eintheilungen, statt, wie gewoͤhnlich, auf
dem Nonius oder Vernier, mittelst des Mikrometers, abgelesen, wodurch, wie Hr. Allan glaubte, viel an Genauigkeit gewonnen wird.
Anmerkungen des Herausgebers.
Hr. Allan theilte den Kreis dieses Theodoliten auf seiner
eigenen Achse ein, und glaubte denselben hierdurch genauer, als nach der
gewoͤhnlichen Art zu machen, um so mehr, da er dadurch gewiß werden konnte:
die Zaͤhne an dem kreisfoͤrmigen Zahnstoke genau an ihre Stelle zu
bringen, indem der halbirte Ring waͤhrend des Einschneidens der Zaͤhne
mittelst einer Tangenten-Schraube, und der dazu eigens verfertigten Einschnitte,
herumgedreht wird. Wenn also die Zaͤhne bis auf eine gewisse Tiefe
eingeschnitten sind, werden die Schrauben, welche die beiden Haͤlften des
Ringes zusammenhalten, herausgenommen, und die obere Haͤlfte um ein Viertel, g, auf der unteren Haͤlfte herumgedreht, und die
Schrauben wieder an ihre Stelle gebracht: das Einschneiden wird fortgesezt, bis die
Zaͤhne tiefer werden, worauf die obere Haͤlfte wieder um ein Viertel
gedreht, und mit dem Einschneiden fortgefahren wird, bis der ganze Ring vollkommen
geschnitten ist. Auf diese Weist wird, wenn irgend ein Unterschied in der
Haͤrte des Metalles an den verschiedenen Stellen des Ringes Statt hat,
wodurch die schneidende Schraube an einer Stelle desselben mehr eingeschnitten
hatte, als an der anderen, die eine Haͤlfte der Zaͤhne durch den
Wechsel auf die andere kommen, und so werden die dikeren Zaͤhne den
duͤnneren zur Haͤlfte gegenuͤber stehen, wodurch sie dann immer
mehr gleich werden koͤnnen. Wirklich werden sie am Ende so gleich, daß, wenn
anders der eine genau uͤber den anderen gebracht wurde, der Rest gleichfalls
genau uͤbereinstimmen wird. Hrn. Allan's
Theilungs-Maschine ist gleichfalls am Rande mit solchen Zaͤhnen versehen, und
wir koͤnnen uns nicht vorstellen, daß, wo die hoͤchste Genauigkeit
nothwendig ist, dieselbe auf irgend eine andere Weise leichter erhalten werden kann.
Sie verdient daher allgemein eingefuͤhrt zu werden.Hieruͤber werden die HHrn. v. Reichenbach
und Frauenhofer zu Muͤnchen am besten
urtheilen. A. d. Ueb.
Tafeln