| Titel: | Beschreibung eines neuen Reductionscirkels, und Anwendung desselben zum Reduciren, Copiren und Construiren von Planen; von P. F. Schiereck. |
| Autor: | Joseph Friedrich Schiereck [GND] |
| Fundstelle: | Band 82, Jahrgang 1841, Nr. LXIII., S. 265 |
| Download: | XML |
LXIII.
Beschreibung eines neuen Reductionscirkels, und
Anwendung desselben zum Reduciren, Copiren und Construiren von Planen; von P. F. Schiereck.
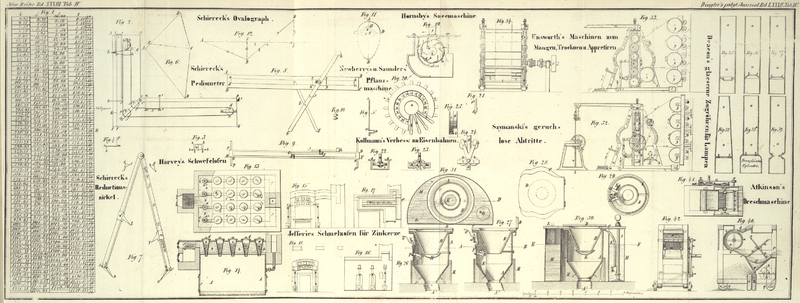
Mit einer Abbildung auf Tab. IV.
Schiereck's neuer Reductionscirkel.
Beschreibung des Instruments.
AB, BC (Fig. 7) sind zwei
metallene geradlinige Schenkel, die in B durch ein
Scharnier verbunden sind. Die Form dieser Schenkel möchte am besten ein dreiekiges
rechtwinkliges Prisma seyn, von dem die eine flache Seite nach Oben gerichtet ist
(sie sind durch die Flächen von AB, BC vorgestellt und
ihr Durchschnitt ist daneben gezeichnet), indem diese Form den Schenkeln die
gehörige Festigkeit gibt, ohne das Instrument schwer zu machen, und Bequemlichkeit
im Handhaben desselben darbietet.
An den Enden AC der beiden Prismen sind Spizen
durch Schrauben an denselben befestigt, und jede Spize bildet eine rechtwinkelige
senkrechte Pyramide, deren Grundfläche Aab oder
Cab und die darauf senkrechte Höhe aD
,
aG ist, und dieß bewirkt, daß die beiden Enden DG genau aneinander liegen, wenn die Schenkel AB
,
BC zusammenkommen. Außer diesen beiden Spizen ist
noch an jedem Schenkel eine Hülse angebracht, die sich an demselben auf- und
abschieben läßt, und durch ein Schräubchen, das auf ein untergelegtes Plättchen
drükt, an jeder beliebigen Stelle des Schenkels kann festgehalten werden, und diese
Hülsen sind mit senkrecht heruntergehenden Spizen versehen, die mit den aD
,
aG parallel und gleich sind. Die Spizen an den
Hülsen können die Form eines halben Kegels haben, wovon die flache Seite nach Innen
zu ist, damit die beiden Enden derselben E und F genau an einander paffen, wenn die beiden Schenkel
zusammengebracht werden. Das Scharnier bei B ist in der
Mitte durchlöchert, und das Loch bildet eine Schraubenmutter, in welche eine
konische Spize von gleicher Höhe wie aD kann
eingeschraubt werden.
Von der Mitte B des Scharniers bis zum Endpunkte a der oberen Fläche BCa theile man die Länge Ba in zwei,
drei, vier... gleiche Theile, beobachte dabei die Vorsicht, die Theilstriche der so
bestimmten Punkte nicht unmittelbar darüberzuziehen, sondern um so viel näher nach
B, als die Entfernung der oberen Kante der Hülse von
dem über F senkrechten Punkte auf derselben beträgt; da
es gerade diese Kante ist, welche die erforderlichen Theile anzeigen soll. Seze nun
auf die Theilstriche aufwärts nach B zu die Zahlen 1/2 ;
1/3 ; 1/4...., und herunterzu nach b die Zahlen 2/3 ;
3/4 ; 4/5....
Es ist stillschweigend vorausgesezt worden, daß die beiden Hülsen auf gleiche Weise
angefertigt wurden, solchergestalt, daß die beiden oberen Kanten nach B zu eine gerade Linie bilden, wenn die beiden Spizen
EF zusammenstehen, und dieses erspart die
gleichartige Eintheilung der oberen Fläche AaB.
Die Fläche AaB und die darauf senkrechte, durch
fd und gi im
Durchschnitt gehende Fläche können daher zu anderweitigen Eintheilungen benuzt
werden, und ich will für das Folgende voraussezen, daß auf der Fläche AaB vom Mittelpunkte B
des Scharniers aus irgend ein Maaßstab aufgetragen ist, zu dessen Vervollständigung
die Hülse ein Plättchen trägt, das den Nonius des Maaßstabes bildet.
Dieß sind alle das Instrument constituirenden Theile, und man wird daraus erkennen,
daß das Ganze der bekannte und oft benuzte Stangencirkel ist, nur mit dem
Unterschiede, daß hier fünf Spizen anstatt zweier angebracht sind, und daß die
Stange in der Mitte ein Scharnier hat, um die Heiden Hälften gleichsam zusammenlegen
zu können.
Anwendung dieses Cirkels zum Reduciren der Karten.
Die vorgehende Beschreibung und Eintheilung des Instruments würde es überflüssig
machen, eine mittelst desselben zu vollführende Reduction von Karten näher zu
beschreiben; die Absicht jedoch, die Vortheile nachzuweisen, welche dieser Cirkel im
Vergleich zu dem bisher üblichen Reductionscirkel gewährt, und die besondere Art der
Handhabung dieses Instruments veranlassen mich, die Anwendung desselben zum
Reduciren ausführlich anzugeben.
Um einen vorgelegten Plan nach einem anderen Maaßstabe abzutragen, wird die Spize,
welche durch B geht, hinweggenommen, und die Hülse am
Schenkel BaC wird mit der Kante nach B zu auf den Theilstrich gebracht, der das verlangte
Verhältniß des Verjüngens oder Vergrößerns angibt, und mit dieser Kante wird die ihr
gleiche Kante der Spize E in gerade Linie gebracht, und
mit Hülfe der Schrauben werden die Hülsen an den bestimmten Stellen
festgehalten.
Ist nun ein vorgelegter Plan z.B. auf die Hälfte des Maaßes zu reduciren, und sind
die Hülsen der Spizen EF zu dem Behufe bei dem
Theilstrich 1/2 festgestellt, dann wird jeder Schenkel des Instruments zwischen dem
Daumen und Zeigefinger einer Hand genommen, so daß der Theil zwischen E und B mit der rechten
Hand, und der Theil FB mit der linken gehalten
wird. Man greift nun mit den Spizen GD die
abzutragende Länge, indem man das Scharnier B etwas in
die Höhe hebt, damit die Spizen EF den Plan nicht
berühren, hält dann mit den Daumen das Scharnier B
herunterzu, damit die beiden Spizen DG in die Höhe
gehen und das Papier, worauf der Plan zu übertragen ist, nicht berühren, und bringt
so die beiden Punkte EF auf das Papier, welche die
halbe Länge von DG abtragen. Dieses Verfahren wird
angewendet, wenn die beiden Hülsen nicht näher als 1/2 zum Scharnier sind; wenn aber
die beiden Hülsen näher zum Scharnier als 1/2 sind, z.B. bei 1/3; 1/4... dann wird
das Instrument zwischen DE und FG auf den Zeigefingern ruhen, da es am
vortheilhaftesten ist, den Schwerpunkt jedes Schenkels zu unterstüzen.
Der etwa nach obiger Angabe auf der Fläche AaB
gezeichnete Maaßstab kann zum Reduciren auch dazu benuzt werden, die Reduction nach
irgend einem beliebigen, auf der Fläche BaC nicht
abgetheilten Verhältnisse zu bewirken, wenn man die ganze Länge zwischen aB in Theilen des Maaßstabes kennt, da man alsdann
die Spize E genau zu dem Punkte bringen kann, der die
Länge aB in das gegebene Verhältniß theilt. Die
verschiedenen Vortheile, welche diese Anordnung gewährt, stellen sich durch die
folgenden Betrachtungen klar heraus, wenn man vorläufig annimmt, daß die Schenkel des hier beschriebenen
Instruments dieselbe Länge haben, als die Schenkel des im Gebrauche stehenden
Reductionscirkels.
Es ist vielfach anerkannt, daß die Länge einer mit einem gewöhnlichen Cirkel zu
messenden Linie nicht größer seyn darf als die Länge des Schenkels vom Cirkel, wenn
man nur eine ziemliche Genauigkeit damit erlangen will, indem ein größerer Winkel
als 60° zwischen den beiden Schenkeln des Cirkels bedeutende
Unzuverlässigkeit herbeiführt. Angenommen, daß ein Plan zur Hälfte des Maaßes soll
reducirt werden, dann wird der Durchschnittspunkt der beiden Schenkel eines
gewöhnlichen Reductionscirkels bei 2/3 der Länge des Schenkels seyn, und man kann
daher nur mit einiger Sicherheit eine Länge = 2/3 des Schenkels zur Hälfte
reduciren, wo hingegen mit dem vorbeschriebenen Instrumente die doppelte Länge des
Schenkels mit der größten Zuverlässigkeit reducirt werden kann, da die Spizen immer
senkrecht bleiben, und a, B, a in gerade Linie gebracht
dasselbe leistet wie bei jedem anderen beliebigen Winkel, und mithin bei derselben
Dimension des Instruments eine dreimal so große Länge mit Zuverlässigkeit zu
reduciren gestattet, als dieß mit dem gewöhnlichen Reductionscirkel geschehen
kann.
Sind ferner die Spizen eines gewöhnlichen Reductionscirkels abgenuzt oder
abgebrochen, welches beim Gebrauche desselben öfters geschieht, und durch Schleifen
oder Einsezen anderer Stüke verbessert worden, dann sind die darauf angebrachten
Abtheilungen unrichtig, was bei dem oben beschriebenen neuen Reductionscirkel nicht
statt hat, indem die Aenderung der Längen der Spizen auf die am Schenkel befindliche
Eintheilung keinen Einfluß hat.
Anwendung des Cirkels zum Copiren der Karten.
Das Copiren von Karten, wenn dieß genau seyn soll, geschieht entweder durch
Eintheilung in Quadrate, oder durch andere Grundlinien, die erst abgetragen werden,
wo dann die Einschnitte in den Seiten der Quadrate oder Grundlinien abgemessen, und
die außerhalb dieser Linien liegenden Punkte dann durch dreispizige Cirkel oder
durch Bogenschlag abgetragen werden. Es ist klar, daß dieses nicht für größere
Distanzen als die Länge eines einzigen Schenkels vom Cirkel geschehen kann, und das
Veränderliche am dreispizigen Cirkel gibt zu vielen Umständen und Unrichtigkeiten
Veranlassung. Das vorgehend beschriebene Instrument kann auf folgende Weise mit
Sicherheit und Bequemlichkeit zum Copiren angewendet werden. Entferne von dem
Instrumente die beiden Spizen D, G und schraube dafür in
B eine Spize ein. Bei Quadraten oder anderen Grundlinien mache die
Entfernung der Spize E von B
der Länge der Seite des Quadrats oder der Grundlinie gleich, und schraube E fest, dann schiebe die Spize F, indem zugleich der Schenkel BC um B gedreht wird, bis die Spize E den abzutragenden Punkt erreicht, und dann wird dieser in den zu
copirenden Plan gebracht.
Für jeden folgenden Punkt ist nur die Spize mit dem Schenkel BC zu ändern, da die Seite der Quadrate oder die
Grundlinie, die zwischen B und E ist, für die übrigen abzutragenden Punkte dieselbe bleibt.
Anwendung des Cirkels zum Construiren von Karten.
Das Construiren von Karten oder das Auftragen gemessener Punkte auf einen dafür nach
verjüngtem Maaßstabe zu zeichnenden Plan geschieht entweder durch die gemessenen
oder berechneten Seiten der Dreieke, oder durch gemessene oder berechnete
rechtwinkelige Coordinaten; beide Arten können durch das oben beschriebene
Instrument leicht ausgeführt werden, wenn man wie zum Copiren gezeigt wurde, die
Spizen D und G hinwegnimmt
und dafür die Spize in B einschraubt.
Sind die Seiten der Dreieke gegeben, dann ist eine der Seiten auf dem anzufertigenden
Plan als Grundlinie aufgetragen, und es kommt nun darauf an, den Durchschnittspunkt
der beiden anderen Seiten zu finden. Zu dem Ende schiebe die Spize E, bis ihre Entfernung von B
der Länge der einen Dreieksseite gleich ist, und eben so schiebe die Spize F, bis FB der Länge
der anderen Dreieksseite gleich ist; bringe dann E in
den einen Endpunkt der Grundlinie und öffne den Schenkel BC so weit, bis F den
anderen Endpunkt der Grundlinie erreicht, so wird die Spize B den Durchschnittspunkt der beiden Schenkel angeben. Soll der Plan
mittelst rechtwinkeliger Coordinaten construirt werden, dann öffne die Schenkel AB, BC so weit, bis sie bei B einen rechten Winkel bilden, welches dadurch leicht zu bewirken ist, daß
man den Längen BE
,
BF
,
EF das Verhältniß 3: 4: 5 gibt, und schraube dann
das Scharnier in B fest, damit keine Aenderung des
Winkels statt habe. Mache dann die Länge zwischen BF der Abscisse gleich, und die Länge zwischen BE der Ordinate gleich; bringe F in den Anfangspunkt der Coordinaten und die Spize B in die Abscissenlinie, so wird E den verlangten Punkt auf dem Plane angeben. Es ist klar, daß dieselbe
Art der Construction auch für schiefwinkelige Coordinaten anzuwenden ist, wenn man
den Winkel EBF dem verlangten Coordinatenwinkel
gleich macht.
Tafeln