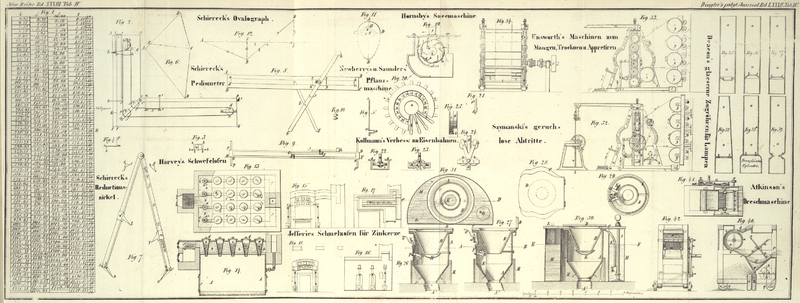
| Titel: | Beschreibung eines Ovalographen, oder eines Instruments, mit welchem man Kreise, Ellipsen und Eilinien beschreiben kann; von P. F. Schiereck. |
| Autor: | Joseph Friedrich Schiereck [GND] |
| Fundstelle: | Band 82, Jahrgang 1841, Nr. LXIV., S. 270 |
| Download: | XML |
LXIV.
Beschreibung eines Ovalographen, oder eines
Instruments, mit welchem man Kreise, Ellipsen und Eilinien beschreiben kann; von
P. F.
Schiereck.
Mit Abbildungen auf Tab.
IV.
Schiereck's Ovalographen.
Zusammensezung des Instruments.
ABCD (Fig. 8) ist eine metallene
Platte, in der ein Ausschnitt abcd ist, in welchem
ein Schieber efgh bewegt werden kann. Durch diesen
Schieber geht in H ein runder Zapfen, in welchem über
dem Schieber ein Stäbchen IK mittelst einer
Schraube festgehalten wird, und unter der Platte ABCD ist an demselben Zapfen ein anderes Stäbchen HG befestigt, und dieß so, daß GIHK in einer senkrechten Ebene liegen.
Unter der Platte ABCD ist in einiger Entfernung mit
derselben eine andere Platte parallel befestigt, und an dieser ist in der Mitte E mittelst eines runden Zapfens ein Stäbchen EF befestigt, das, sich um diesen Zapfen drehend,
zwischen den beiden Platten durchgehen kann.
Die beiden Stäbchen EF, HG sind in L
vermittelst der Vorrichtung in (Fig. 10) miteinander
verbunden. Diese Vorrichtung besteht aus zwei Hülsen, die mittelst eines runden
Zapfens, um den sich die eine Hülse drehen kann, übereinander befestigt und an der
Seite mit Schräubchen versehen sind. In der untern Hülse wird das Stäbchen EF mittelst des Schräubchens festgehalten, und
dasselbe geschieht in der obern Hülse mit dem Stäbchen GH, wodurch denn die beiden Stäbchen in jedem beliebigen Punkte
miteinander verbunden werden können, und sich in dem Verbindungspunkte zu drehen
vermögen. Wird am Stäbchen GH der runde Stift, der
durch den Schieber in H geht, befestigt, und dieser
Stift trägt über H eine mit einem Schräubchen versehene
Hülse, die GH parallel gerichtet ist, und in
welcher das Stäbchen IK geht, dann ist die oben
verlangte Bedingung, daß GH, IK in einer senkrechten Ebene seyen, erfüllt.
Zur bessern Versinnlichung ist (Fig. 9) das Profil durch
die Mitte der Platte ABCD (Fig. 8) dargestellt, und
für die verschiedenen Theile sind hier dieselben Buchstaben wie oben gebraucht
worden.
CD ist das Profil der oben beschriebenen Platte
ABCD, mit der parallel die Platte MN mittelst der senkrechten Theile DN, CM verbunden
ist und zwei breite Metallstüke OP können sowohl
in die Platte MN, als auch in die Platte CD als Füße eingesezt werden.
Die Stäbchen EF, GH, IK sind nach obiger Stellung hier
verjüngt eingezeichnet, und ist dabei noch zu bemerken, daß bei K eine Hülse ist, in der ein Bleistift oder eine
Reißfeder mittelst einer Schraube befestigt werden kann.
Dieß sind alle Theile, aus denen das Instrument zusammengesezt wird, deren
Dimensionen von der zu beabsichtigenden Anwendung abhängen, und wonach auch die
Stärke der einzelnen Glieder zu bemessen ist.
Anwendung des Instruments zum Construiren von Ellipsen und
Kreisen.
Ist die große und die kleine Achse der zu beschreibenden Ellipse gegeben, dann wird
der vierte Theil des Unterschiedes der beiden Achsen die Länge angeben, die man vom
Mittelpunkte E nach L zu
nehmen hat und die der von H nach L gleich ist, wodurch das Feststellen der Hülsen (Fig. 10) bestimmt wird.
Die Länge HK wird der halben kleinen Achse gleich
gemacht, und wenn dieß geschehen ist, dann bringt man die Mitten von AB und BC über
die Linie, welche die Lage der großen Achse angibt und beschreibt mittelst des
Stiftes in K die verlangte Ellipse, indem man den Punkt
L zwischen den beiden parallelen Platten durchstößt,
wenn E, L und K in gerader
Linie sind.
Ist die große Achse größer als die Länge der Platte ABCD, bann werden die beiden Füße OP mit
der Platte MN verbunden und das Stäbchen IK geht über der Platte ABCD her und führt den Stift K um ABCD herum; ist
aber die große Achse kleiner als die Länge des Instruments, dann werden die beiden
Füße OP mit der Platte ABCD verbunden und der Stift K geht unter derselben her. Macht man HK der Länge des Halbmessers eines Kreises gleich
und bringt EF und GH übereinander, dann beschreibt der Punkt K
den verlangten Kreis.
Das Verfahren ist so einfach, daß es keiner weitern Erörterung bedarf, und die
kleinen Handgriffe zum Handhaben des Instruments wird Jeder nach einigen Versuchen
leicht ausfinden.
Anwendung des Instruments für Eilinien.
Die Eilinien unterscheiden sich von den Ellipsen darin, daß ihre größte Breite nicht
gerade in der Mitte der großen Achse ist, und es ist daher nöthig, außer der großen
und kleinen Achse noch den Punkt in der großen Achse zu kennen, wo die größte Breite
seyn soll.
Es sey nun (Fig.
11) AB = a
die große Achse; CD = b die kleine Achse; EF = c die Entfernung des Durchschnitts der kleinen und großen Achse vom
Mittelpunkte der großen Achse der zu beschreibenden Eilinie; so ist für das Anwenden
des Instrumentes folgendes Verfahren zu beobachten.
Die Länge HK werde die Hälfte der kleinen Achse =
b/2; LH
= (a – b)/2 = dem
halben Unterschied der beiden Achsen;
Textabbildung Bd. 82, S. 272
oder wenn man dieß durch eine geometrische Construction finden
will, trage die Länge DE von A nach G und mache EI = FG; ziehe
IF und mache EH = EF und beschreibe mit FH den Bogen IK,
bis er die Linie AF in K trifft; ziehe HI und mit dieser die
Parallele KL, so ist LF die verlangte Länge für EL (Fig. 8). Es
können hiebei Fälle eintreten, wo der Punkt K über H hinausfällt, wobei dann der Punkt L in der Verlängerung von FI seyn wird.
Bei den Eilinien wird der Stift in K immer unter der
Platte ABCD zu bewegen seyn, und es wird daher die
Länge der großen Achse immer kleiner als die Länge des Instruments seyn müssen.
Theoretische Auseinandersezung des beschriebenen
Ovalographen.
Mit der Linie AE sey in A eine andere Linie AB = a solchergestalt verbunden, daß diese sich um A drehen kann (Fig. 12). In B sey ebenfalls eine um diesen Punkt sich drehende Linie
BC = b angebracht,
jedoch so, daß der Punkt genöthigt ist auf der Linie AE zu bleiben, so wird die Verlängerung von BC, oder auch irgend ein Punkt in derselben beim Fortbewegen dieser Linie
eine Curve beschreiben, deren Form von den Verhältnissen der Linien abhängen wird.
Sezt man die Verlängerung von BC, nämlich die CD = c und fällt von
D und B auf AE die Perpendikel DE, BF, so sind AF, BF die
Coordinaten der durch den Punkt B zu beschreibenden
Curve, die ein Kreis seyn wird, und AE = x, DE = y sind die Coordinaten der durch den Punkt D entstehenden Curve.
Die Dreieke BCF, CED sind ähnlich, wodurch
Textabbildung Bd. 82, S. 272
und
Textabbildung Bd. 82, S. 272
Hieraus ergibt sich für den Fall, wenn a = b ist, also
Textabbildung Bd. 82, S. 273
daß die Curve eine Ellipse ist, deren kleine Achse = 2 c, große Achse = 2 (2 b +
c) ist, und wenn c
negativ wird, d. i. wenn es zwischen BC oder über
B hinaus liegt, bann ist die große Achse = 2 (2 b – c).
Wird b kleiner als a, dann
entsteht eine Eilinie, und ist b größer als a, dann beschreibt der Stift in K eine Art Lunula.
Tafeln