| Titel: | Beschreibung eines Wasserschöpfrades; von Niel. |
| Fundstelle: | Band 98, Jahrgang 1845, Nr. LXXV., S. 267 |
| Download: | XML |
LXXV.
Beschreibung eines Wasserschoͤpfrades; von
Niel.
Aus dem Mém. de l'officier du génie durch Crelle's Journal fuͤr die
Baukunst Bd. XXI S. 246.
Mit Abbildungen auf Tab.
IV.
Niel, über ein vortheilhaftes Wasserschöpfrad.
Diese Wasserschöpfmaschine ist, wie man aus der hier folgenden Beschreibung sehen
wird, augenscheinlich ungemein praktisch, und ihre
Wirkung ist, wie sich aus den am Schluß dieses Aufsazes mitgetheilten Erfahrungen
ergibt, in Vergleich gegen andere Maschinen vorzüglich. Die Maschine hat über 80
Proc. Nuzeffect gegeben, und ein Rad, welches täglich in 10 Stunden 187,722 Kubikfuß
Wasser 1 Fuß hoch oder z. B. 23,440 Kubikfuß Wasser 8 Fuß hoch hebt, hat nur 160
Thlr. und täglich, mit dem Lohn der Arbeiter, noch nicht 3 Thlr gekostet. 1000
Kubikfuß Wasser damit 8 Fuß hoch zu heben, kosteten nur 3,6 Sgr. Die Maschine
verdient also besondere Berüksichtigung und würde auch in Deutschland bei
Grundbauen, wo es in der Schöpfgrube nicht an Raum fehlt, häufig von bedeutendem
Nuzen seyn können, wenn man sich ihrer bedienen will. Deßgleichen würde sie
vorzüglich passend seyn bei der Entwässerung von Ländereien, wo das Wasser nicht
sehr hoch zu heben ist und wo man sie dann auch durch die Kraft des Windes, oder des
Dampfs, oder, wenn Wassergefälle in der Nähe ist, durch die Kraft des Wassers in
Bewegung sezen lassen kann.
Die Baue zur Erweiterung der Festungswerke von Bayonne zwischen dem alten Schloß und
dem Bar und Dour in den Jahren 1834 und 1835 erforderten fortgeseztes Ausschöpfen
von Wasser, welches sehr kostspielig wurde. Man fand sich deßhalb bewogen auf eine
Maschine zu denken, die einem anhaltenden und lange fortgesezten Gebrauch
widerstehen könnte, und welche von Menschen auf die vortheilhafteste Weise, nämlich
durch ihr Gewicht, in Bewegung zu sezen sey.
Von allen Wasserschöpfmaschinen sind Räder die festesten.
Sie sind um ihre Achse im Gleichgewicht; und da sie selbst zugleich die Stelle der
Schwungräder vertreten, reicht schon eine geringe Geschwindigkeit hin, die Bewegung
gleichförmig zu machen.
Die Räder mit Kasten (à tympans)haben zwei Uebelstände.
Der eine ist, daß sie das Wasser nur bis auf die Höhe ihrer Achse heben, was z. B.
in Bayonne einen Durchmesser des Rades von beinahe 18 Fuß erfordert haben würde; der
zweite ist, daß die Kraft, sie in Bewegung zu sezen, nach der Tiefe der Eintauchung
des Rades veränderlich ist.
Diejenigen Räder, welche das Wasser bis über ihre Achse
heben, haben zwar den erstgenannten Uebelstand nicht, aber alle uns bekannten haben
den zweiten. Denn die Wassermasse, welche sie fassen, bleibt dieselbe, während die
Kraft, um diese Masse zu heben, mit der Höhe des Hubes wechselt.
Das Rad, welches wir hier beschreiben wollen, hat die beiden Mängel nicht. Fünf Mann
hoben in einer Stunde mit demselben 3234½ Kubikfuß Wasser 8 Fuß hoch (also 7,
19 Kubikfuß in der Secunde 1 Fuß hoch; thut etwa preußische 95 Pfd. Hub auf den Mann
in der Secunde 1 Fuß hoch). Vermindert sich die Höhe des Wasserspiegels in der
Schöpfgrube, so ändert sich die gehobene Wassermenge; aber die nöthige Kraft, das
Rad in Bewegung zu sezen, bleibt dieselbe.
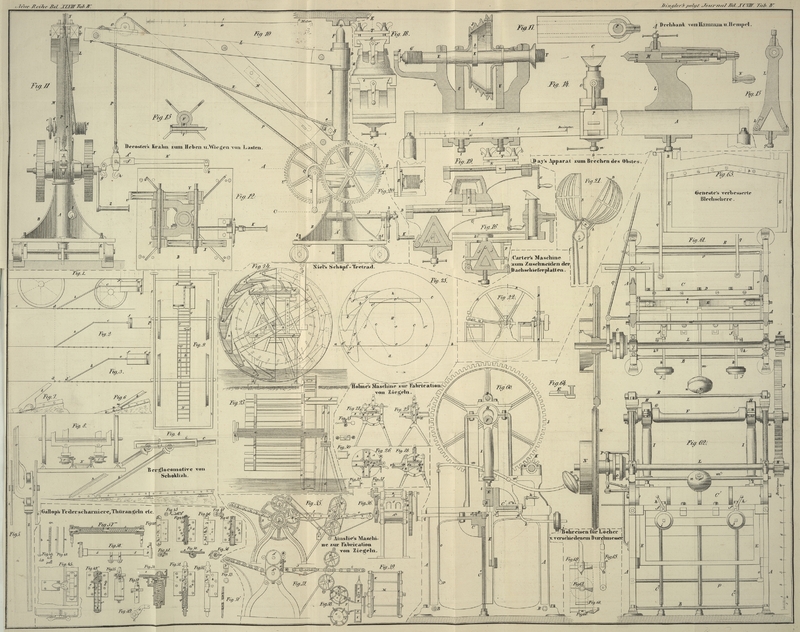
Fig. 23 und
24
stellen dieses Schöpf-Tretrad im 50ften Theil der natürlichen Größe vor.
a, a ist die hölzerne Achse, an den Enden mit eisernen
Zapfen. b, b sind die beweglichen Zapfenlager. c, c sind die Arme, durch welche das Tretrad so wie die
kreisförmigen Schaufelscheiben an der Achse befestigt sind. d, d sind die Gerüste, auf welchen die Stiele stehen, zwischen denen die
Zapfenlager b auf und nieder gestellt werden können. Die
Stiele haben Löcher, durch welche eiserne Bolzen gestekt werden können, um die
Zapfenlager horizontal zu stellen und das Rad auf die nöthige Höhe zu heben. e, e sind Klappen, welche sich durch ihr Gewicht öffnen,
wenn die Schaufeln niedergehen, und sich schließen, wenn sie emporsteigen. f, f ist die Rinne, in welche die Schaufeln das Wasser
ausgießen. g, g ist die horizontale Stange, an welcher
die Männer in dem Tretrad mit den Händen sich festhalten.
Es ist nicht schwierig, das Verhältniß der aufgewendeten Kraft an dem Rad zu der
hervorgebrachten Wirkung durch eine Gleichung darzustellen, in welche die
verschiedenen Dimensionen des Rades eingesezt werden. Aus dieser Gleichung läßt sich
schließen, daß der Halbmesser der Wellzapfen, die Höhe h
des innern Umfangs des Rades über dem Boden der Schaufeln, und die Geschwindigkeit
des Rades so klein seyn müssen, als möglich.
Wellzapfen von 1½ Zoll im Durchmesser sind stark genug, um ein Rad für
7–8 Mann zu tragen. Aber die Zapfen müssen mittelst ihres vierekigen Theils
sehr genau an die Welle befestigt werden; denn wenn sie im geringsten lose werden,
verliert das Rad sein
Gleichgewicht. Der Werth von h hängt von der Form der
Schaufeln ab.
Diese Form der Schaufeln muß zwei Bedingungen erfüllen. Die erste ist, daß möglichst die gleiche Kraft zur
Bewegung des Rades nöthig sey, wie tief es auch eintauchen möge. Bei dem ersten Rad,
welches man zu Bayonne baute, war diese Bedingung nicht gehörig berüksichtigt, und
es war nun nicht möglich, das Rad in Bewegung zu sezen, wenn es bis zu seiner Welle
eintauchte. Die zweite Bedingung ist, daß die Schaufeln,
wenn sie ihre volle Ladung von Wasser eingenommen haben, dasselbe nicht eher
ausschütten, als bis sie bei der Ausgußrinne angelangt, oder darüber hinausgekommen
sind.
Um die erste Bedingung zu erfüllen, müssen 1) die
Schaufeln noch immer so viel Wasser als möglich schöpfen, wenn wenig in der
Schöpfgrube steht; weßhalb ihre äußere Fläche dem äußern Rande der Radkränze so nahe
seyn muß, als es irgend angeht. 2) Müssen sich die Schaufeln nicht überladen, wenn
sie tief eintauchen; was dadurch erreicht werden wird, wenn man sie nach oben zu
verengt, das heißt, wenn man den Punkt g (Fig. 25) dem
Punkt d möglichst nähert und die Zahl der Schaufeln so
groß macht, als es sich thun läßt.
Die zweite Bedingung erfordert, daß 1) die Schaufel ihr
Wasser so schnell als möglich ausgieße, und daß deßhalb alles Wasser in der Schaufel
möglichst zugleich in Bewegung komme; was nur geschieht, wenn die innere Wand k, g der Schaufel eben ist.
2) erfordert die zweite Bedingung, daß die innere Wand der Schaufel eine solche Lage
habe, daß die Schaufel das Wasser nicht eher als in die Ausgußrinne ausschütte; was
denn die Höhe h bestimmt.
Es sey a b (Fig. 25) die größte Höhe
des Wassers in der Schöpfgrube. Die Schaufel wird dann, wenn sie sich aus dem Wasser
hebt, die Masse d′ k′ h′
aufgenommen haben. Ist nun ferner g e der obere Rand der
Aufgußrinne, so wird die Schaufel nur die Masse e k g
oder e′ k′ g′ bis dahin bringen;
das etwa Uebrige wird unterwegs verloren gehen. Damit nichts verloren gehe, müssen
also die Querschnitte d′ k′ g′ und
e′ k′ g′ und folglich die
Dreieke d′ e′ f′ und g′ h′ f′ einander gleich seyn.
Diese Bedingung wird erreicht, entweder dadurch, daß man die Schaufeln mehr
ineinander hineintreten läßt, oder daß man die Höhe der Aufgußstelle verändert.
Endlich müssen die Schaufeln auch all' ihr Wasser in die Ausgußrinne schütten. Die
Erfahrung hat gezeigt, daß diese Bedingung bis zu einer Geschwindigkeit von etwa 23
Zoll in der Secunde erreicht wird, und insofern der Boden g
k der Schaufel schon über die horizontale Lage hinausgekommen war, in dem Augenblik, wo
der Punkt die Verticalebene durch die Radachse passirte.
Um die Schaufeln zu zeichnen, muß man also den größten und den kleinsten Werth von
H kennen. Man nimmt dann erst irgend einen Werth von
h an und sucht vermittelst des Obigen in einer
Zeichnung wie Fig.
25 denjenigen Querschnitt der Schaufeln, der, wenn n Schaufeln zugleich voll sind, und die Fläche d′ k′ h′ gleich s ist,
für das Product n s (H +
½ h) möglichst stets eine und dieselbe Größe
gibt, was auch H seyn mag. Findet sich mit dem
angenommenen h das verlangte Ergebniß nicht, so nimmt
man ein größeres h an; was dann einen größern Halbmesser
des Rades verlangt, und wiederholt die Versuche. Das Begehrte wird um so leichter zu
erzielen seyn, je größer der Spielraum ist, den man dem h gibt; aber dieß geschieht dann auch auf Kosten des Nuzeffects. Zu
bemerken ist noch, daß wegen der Bewegung des Rades die
Schaufeln etwas mehr Wasser aufnehmen, als geschehen
würde, wenn das Rad still stände. Bei 1 Fuß
Geschwindigkeit füllen sich die Schaufeln so, als wenn das Wasser 2 Zoll höher
stände, als es wirklich steht; bei 2 Fuß Geschwindigkeit so, als wenn das Wasser 4
Zoll höher stände.
So lange das Wasser in der Schöpfgrube nicht die innere Oeffnung der Schaufeln
bedekt, entweicht die Luft aus der Schaufel auf der einen Seite, während das Wasser
auf der andern eintritt; steht aber das Wasser höher, so muß man der Luft einen
andern Ausweg verschaffen. Zu dem Ende befindet sich an dem Boden jeder Schaufel
eine kleine Klappe, welche vermöge ihres Gewichts sich öffnet oder schließt, je
nachdem sie die Luft entweichen lassen, oder das Wasser zurükhalten soll.
Die angemessenste Geschwindigkeit des Radumfangs liegt zwischen 1 und 2 Fuß in der
Secunde. Für eine geringere Geschwindigkeit verliert die Bewegung an
Gleichförmigkeit. Bei einer größern Geschwindigkeit müssen sich die Menschen im
Tretrade zu schnell bewegen.
Es ist zu bemerken nöthig, daß die Wirkung der Menschen im Tretrade, wenigstens
innerhalb bestimmter Gränzen, welche wir angeben werden, von der Geschwindigkeit der
Maschine unabhängig ist. In der That ist diese Wirkung, für jeden Schritt der
Männer, gleich ihrem Gewicht multiplicirt mit der senkrechten Höhe einer Staffel.
Ständen die Menschen in der durch die Achse gehenden waagrechten Ebene, so würde die
senkrechte Höhe der Staffel der Höhe der Staffel selbst gleich seyn; ständen sie
dagegen auf dem obersten Punkt des Rades, so würde die senkrechte Höhe Null seyn. Die
Arbeiter finden leicht von selbst zwischen diesen beiden äußersten Punkten
denjenigen, welcher für ihre Wirkung der vortheilhafteste ist. Wollen sie erst das
Rad in Bewegung sezen, so steigen sie bis zur Achse hinunter, und dann wieder
hinauf, so wie die Geschwindigkeit zunimmt. Läßt man einen Mann zu Hülfe kommen, um
die Geschwindigkeit zu verstärken, so steigen sie mechanisch ein wenig höher auf das
Rad hinauf, damit die Vergrößerung der Geschwindigkeit sie nicht zu sehr ermüde.
Wenn die Meeresfluth oder das Wasser schnell in der Schöpfgrube stieg, strengten sich
die Leute ¾ bis eine ganze Stunde lang so an, daß die Höhe, um welche jeder
Arbeiter in der Secunde seinen Schwerpunkt in die Höhe hob, oder m = 7⅔ Zoll war; sank dagegen das Wasser, so war
m nur 4–4¼ Zoll. Es wird nach unserer
Meinung der von Navier angegebene Werth 5 5/4 Zoll von
m, der aus umfassenden Beobachtungen gefunden worden
ist, im Durchschnitt für eine ganze Tagesarbeit angenommen werden können. Als erst
die Maschine gebaut war, beklagten sich die Arbeiter über Ermüdung in den Beinen.
Späterhin aber gefiel ihnen die Arbeit, und es gab einige darunter, die den ganzen
Tag und die folgende Nacht sie aushielten.
Wir schließen aus allem diesem, daß man im Mittel die Geschwindigkeit des Rades v = 17,20 Zoll = 1,434 Fuß und m = 5,73 Zoll = 0,478 Fuß sezen kann.
Das Rad hat 20 Schaufeln. Der Querschnitt jeder Schaufel ist 0,8436 Quadratfuß; die
Radkränze stehen 1,02 Fuß von einander, also faßt jede Schaufel 0,8605 Kubikfuß
Wasser. Bei einem Umlauf des Rades werden daher 20 . 0,8605 = 17,21 Kubikfuß Wasser
gehoben, an Gewicht 66 . 17,11 = 1136 Pfd. Die Höhe H
ist 8¼ Fuß und h ist 1 1/5 Fuß. Der Durchmesser
des Kreises, dessen Geschwindigkeit v bezeichnet, ist
10, 83 Fuß und die Zeit eines Umlaufs 23,68 Secunden. Hieraus ergibt sich, daß sechs
Mann nöthig sind, um die 17,21 Kubikfuß Wasser in 23,68 Secunden 8¼ Fuß hoch
zu heben.
Wenn die Zahl der Arbeiter bestimmt ist, so ergibt sich daraus die nöthige Breite des
Tretrades. Ein Mann braucht 15 Zoll Breite der Staffeln; also muß das Tretrad für
sechs Mann 6 . 15 Zoll = 7½ Fuß breit seyn. In Fig. 23 ist das Tretrad
zu schmal gezeichnet. Es war auf 1 Fuß Geschwindigkeit und auf 160 Pfd. Gewicht
eines Mannes berechnet, was in der dortigen Gegend nicht passend ist.
In dem Rad welches die Figuren vorstellen, befinden sich
an Fichtenholz
2081
Pfd.
an Eichenholz
400
—
an Eisen
277
—
––––––––––
Das Rad wiegt also
2758
Pfd.
Für H = 8, 25 Fuß sind 7 Schaufeln zugleich voll und enthalten 395 Pfd. Wasser. Außerdem ist das Gewicht der
sechs Arbeiter 900 Pfd. Es ist also der gesammte Zapfendruk = 4053 Pfd.
Die Versuche mit dem durch die Figuren vorgestellten Rad
haben folgendes Verhältniß der Kraft zum Nuzeffect ergeben.
Als fünf Mann angestellt waren, welche im Durchschnitt jeder 151½ Pfd. wogen,
maß man wiederholt das Wasser, welches das Rad in die Höhe brachte. Es hob in l
Secunde 48,13 Pfd. Wasser 8 Fuß hoch und machte in 42 Secunden einen Umlauf. Die
Arbeiter hoben in der Secunde ihren Schwerpunkt um 0,6 Fuß. Die Wirkung jedes
Arbeiters war also 151½ . 0,6 = 90,9; dagegen der Nuzeffect war 1/5 . 48,13 .
8 = 77,0.
Man ließ nun einen Mann mehr auf das Rad steigen. Dann machte das Rad in 25 Secunden
einen Umlauf; die Arbeiter hoben sich um 0,637 Fuß in der Secunde, und die Wirkung
eines jeden war also 151½ . 0,637 = 96,5. Das Rad hob jezt in der Secunde 60,
16 Pfd. Wasser 8 Fuß hoch; also war der Nuzeffect jedes Arbeiters jezt ½ .
60,16 . 8 = 80,21.
Bei dem ersten der beiden Versuche war also der Nuzeffect 83, bei dem zweiten 82
Proc. von der angewendeten Kraft.
Das Rad, welches diese Wirkung leistete, hatte nur 160 Thlr. gekostet, und diente
schon mehrere Monat. Es wird ganz hinreichend seyn, wenn man zu der Erhaltung und
Erneuerung desselben 8 Sgr. auf den Arbeitstag rechnet. Die Wirkung eines Arbeiters
kann dem Obigen zufolge für einen Arbeitstag von 10 Stunden auf
0,478 . 150 . 10 . 60 . 60 = 2581200
gerechnet werden. Rechnet man hievon für den Nuzeffect 80
Proc., so beträgt derselbe 2,064,960, also 2,064,960/66 = 31,287 Kubikfuß Wasser 1
Fuß hoch gehoben. Der Taglohn eines Arbeiters zu Bayonne ist 11, 80 Sgr. Die
Erhaltung der Maschine, zu 8 Sgr. täglich, beträgt auf jeden der sechs Arbeiter 1,33
Sgr.: also kosten 31,287 Kubikfuß Wasser 1 Fuß hoch zu heben 12,80 + 1,33 = 14,13
Sgr. Die sechs Arbeiter würden also täglich in 10 Stunden 6 . 31,287 = 187,722
Kubikfuß Wasser 1 Fuß hoch oder 182,722/8 = 23,440 Kubikfuß Wasser 8 Fuß hoch zu
heben vermögen, und
dieß würde 6 . 14,13 = 84,78 Sgr. oder noch nicht 3 Thlr. kosten. 1000 Kubikfuß
Wasser 1 Fuß hoch zu heben würde
Textabbildung Bd. 98, S. 273
= 0,451 Sgr., und 8 Fuß hoch zu heben, 3,6 Sgr. kosten.
Tafeln