| Titel: | Theorie der Haupt- oder Triebfeder einer Taschenuhr; von Alex. Young zu Camden in den Vereinigten Staaten. |
| Fundstelle: | Band 128, Jahrgang 1853, Nr. LXXIX., S. 338 |
| Download: | XML |
LXXIX.
Theorie der Haupt- oder Triebfeder einer
Taschenuhr; von Alex.
Young zu Camden in den Vereinigten Staaten.
Aus dem Civil Engineer and Architect's Journal, März 1853,
S. 86.
Mit Abbildungen auf Tab.
V.
Young's Theorie der Haupt- oder Triebfeder einer
Taschenuhr.
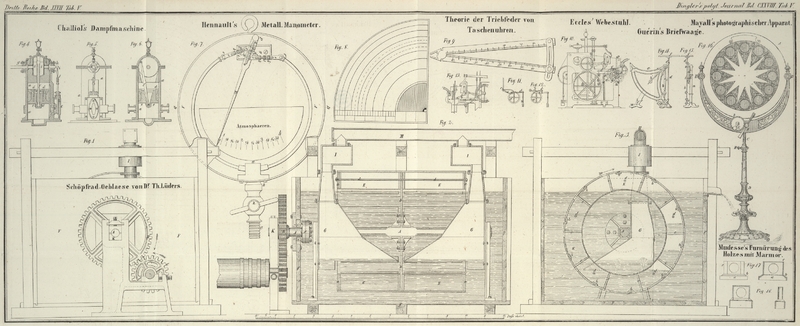
Fig. 8 ist die
vergrößerte Skizze von dem Quadranten der Federtrommel einer Taschenuhr. Dieser
Quadrant ist in neun gleiche Räume getheilt, von denen acht die Theorie der
Federwirkung zeigen. Der centrale Raum ist für die Spindel oder den Stift bestimmt
und hat 1/3 von dem Durchmesser der Trommel. Unter der Figur befindet sich ein
Maaßstab von 24 gleichen Theilen, welche der Dicke der Feder entsprechen, die nach
ihrem Verhältniß zu dem Durchmesser der Trommel bestimmt wird; wir wollen annehmen,
dieses Verhältniß sey 72 zu 1. Zwei Windungen der Feder, die in dem äußern Raum
befindlich sind, werden denselben alsdann ausfüllen, und wenn sie auf die Spindel
aufgewickelt ist, so wird sie den inneren Raum ausfüllen und fünf Windungen machen.
Wenn die Feder, wie gewöhnlich, an der Trommel und Spindel befestigt ist, so
veranlaßt sie drei Umdrehungen, um sich wieder zu ihrer ersten Stellung auszudehnen.
Neunzehn Windungen werden die sieben äußeren Räume ausfüllen; und wenn die Feder
aufgezogen ist, so werden die sieben inneren Räume 22 Windungen enthalten; sie haben
dieselbe Differenz und dieselben Umdrehungen wie oben, jedoch mit größerer Kraft und
mit einer gleichförmigeren Wirkung. 9 1/6 Windungen werden die vier äußeren Räume
ausfüllen, und wenn die Feder aufgezogen ist, so werden die vier inneren Räume 5 2/3
Windungen mehr enthalten. Die Feder hat die größte Wirkung, wenn sie vier Räume oder
die Hälfte von der Trommel füllt; wenn sie sich bis zur Mitte des fünften Raumes ausdehnt,
so verliert sie 1/16 bei einer Ausdehnung bis zu den ganzen fünf Räumen geht 1/6 von
einer Umdrehung verloren, allein die Feder gewinnt an Kraft und überträgt dieselbe
gleichförmiger. Ein Maaßstab für irgend eine Dicke der Feder kann an derselben Figur
angebracht werden.
Die folgende Tabelle gibt die Halbmesser der Kreise an, welche die Federtrommel in
neun gleiche Räume theilen; ebenso die dadurch bewirkten Umdrehungen, die gleich der
Anzahl von Windungen sind, welche die Feder, wenn sie auf der Spindel aufgezogen
ist, über die Zahl hinaus hat, wenn sie gegen die Peripherie ausgedehnt ist.
Halbmesser der Kreise.
Umdrehungen.
Halbmesser der Kreise.
Umdrehungen.
36,000
–
25,455
5597
33,940
2910
24,000
5392
31,754
4531
20,777
4531
29,392
5392
16,970
2910
28,142
5597
12,000
–
26,832
5664
–
–
Fig. 9 zeigt
die Form der Kaliberzirkel mit Sector. Die langen Schenkel sind 4 Zoll lang und von
dem Mittelpunkt des Scharniers beiderseits in 100 gleiche Theile getheilt; die 60,
70 und 80 gegenüber befindlichen Theilungen sind mit 4, 5 und 6 bezeichnet und
entsprechen der Anzahl der Trommelumgänge. Eine Klammer nebst Stellschraube
gestattet eine Oeffnung des Zirkels bis zu 1 Zoll. Die kurzen Schenkel des Zirkels
sind 4/10 Zoll lang und öffnen sich bis auf 1/10 Zoll, oder wie 10 zu der Entfernung
zwischen zwei entsprechenden Zahlen auf den langen Schenkeln des Zirkels.
Die folgende Tabelle zeigt, wie viele Umdrehungen der Trommel durch verschiedene
Dicken der Feder hervorgebracht werden. Es ist ein Abzug für die Befestigung der
Enden und für den weichen Theil der Feder gemacht, der sich nicht von der Spindel
abwickelt; dieser Abzug kann 1/3 Umlauf für eine Feder von 1/80, und 3/4 für eine
solche von 1/60 des Durchmessers betragen.
Windungen der Feder zu
dem Durchmesser der Trommel.
Umdrehungen
nach der
Theorie.
Umdrehungen nach dem
Experiment.
60
4,72
4,0
62
4,88
4,2
64
5,04
4,4
66
5,19
4,6
68
5,35
4,8
70
5,51
5,0
72
5,66
5,2
Windungen der Feder zu
dem Durchmesser der Trommel.
Umdrehungen
nach der
Theorie.
Umdrehungen nach dem
Experiment.
74
5,82
5,4
76
5,98
5,6
78
6,14
5,8
80
6,30
6,0
82
6,46
6,2
84
6,61
6,4
Um eine Feder für irgend eine Anzahl von Umdrehungen der Trommel auszuwählen, öffne
man den Sector bis zum Halbmesser der Trommel an der Zahl der Scala für die
erforderlichen Umdrehungen, und es wird alsdann die Oeffnung der kurzen Schenkel
genau fünf Windungen der Feder von passender Dicke zulassen.
Um das Gewicht einer Feder für irgend eine Größe der Trommel zu finden, nehme man den
innern Durchmesser derselben in Hunderttheilen eines Zolles ab, welches dadurch
geschieht, daß man den Sector auf die Länge des Durchmessers öffnet; man lege dann
die Trommel zwischen die langen Schenkel an die den Hunderttheilen
gegenüberstehenden Zahlen der andern Scala, welche alsdann den Durchmesser angeben
werden. Die Breite der Feder wird auf dieselbe Weise bestimmt. Man suche alsdann in
der folgenden Tabelle den Durchmesser der Trommel auf, multiplicire die demselben
gegenüberstehende Zahl mit der Breite der Feder, so erhält man das Gewicht in
Troy-Grains für eine Feder, welche 9/16 der Trommel ausfüllt. Die Tabelle
wird so construirt, daß man die Oberfläche der Spindel von der Oberfläche der
Trommel in Hunderttheilen eines Zolles abzieht; 9/16 des Rests multiplicirt mit 1900
(Grains, welche 1 Kubikzoll Uhrfeder wiegt), geben die Zahlen in der Tabelle. Wenn
die Spindel weniger als 1/3 von der Trommel ausmacht, so schließen die kurzen
Schenkel des Zirkels dicht an, und die Feder hat ihr volles Gewicht; ist die Spindel
aber stärker, so schließen die Zirkelschenkel nicht dicht an und die Feder hat ein
etwas zu geringes Gewicht.
Textabbildung Bd. 128, S. 340
Tabelle des Trommeldurchmessers in
Hunderttheilen eines Zolles; Gewicht der Feder in Troy-Grains für jeden
Hunderttheil eines Zolles in der Breite
Die nächste Tabelle ist nach Versuchen mit einer 12/100 Zoll breiten Feder
construirt, welche fünf Räume oder 5/9 einer Trommel von 67/100 Zoll Durchmesser
ausfüllt, deren Federdicke 1/78 beträgt und 45 Grains wiegt. Um die Trommel wurde
die Kette gewickelt, welche mit einer Schale für Gewichte versehen und an der
Spindel befestigt war, worauf durch Einlegen von Gewichten die Kette sich
abwickelte. Das zu jeder Umdrehung erforderliche Gewicht wurde bemerkt und in die
Tabelle eingetragen.
Zugkraft in Unzen Troy-Gewicht.1 Unze Troy-Gewicht = 480 Grains.
Textabbildung Bd. 128, S. 341
Räume gefüllt; Summa; Zahl v.
Umdrehungen
Die Feder wurde alsdann herausgenommen und ihre Länge reducirt, indem man 4 1/2
Grains abbrach. Nun wurde sie wieder befestigt und das vorherige Verfahren
wiederholt, wodurch die zweite Colonne der Tabelle entstand. Es wurden alsdann
weitere 4 1/2 Grains abgebrochen, so daß nun die Feder noch 36 Grains wog. Das wie
vorher angewandte Gewicht gab die Zahlen der dritten Colonne in der Tabelle, woraus
man die Stärke der Federn am Ende einer jeden von den fünf Umdrehungen ersieht,
sowohl wenn sie 5, als wenn sie 4 1/2 oder 4 Räume ausfüllt.
Die Summe jeder Colonne gibt das Gewicht an, welches auf eine der Peripherie der
Trommel gleiche Höhe emporgehoben worden ist. Die größte Kraft wird erlangt, wenn
die fünf Räume ausgefüllt sind; mit vieren werden freilich die fünf Umdrehungen noch
vollständig ausgeführt werden, allein sie sind nicht hinreichend, um den
Kraftverlust auszugleichen.
Die Federn der besten Taschenuhren füllen 4 1/2 Räume aus, und haben eine Umdrehung
über der erforderlichen Zahl, um eine Ausdehnung zu gestatten und um noch einen
freien Raum zu haben. Der Kaliberzirkel, die Tabelle (welche auf Kartenpapier copirt
werden kann) und eine feine Waage mit Graingewichten sind die ausreichenden Apparate, um eine Feder
auszuwählen, welche die erforderliche Anzahl von Umdrehungen und die größte Kraft
bei der gegebenen Räumlichkeit der Trommel hat.
Tafeln