| Titel: | Ueber Reichenbach's Distanzmesser; vom Ministerialrath Dr. Steinheil. |
| Fundstelle: | Band 129, Jahrgang 1853, Nr. XCII., S. 408 |
| Download: | XML |
XCII.
Ueber Reichenbach's Distanzmesser; vom Ministerialrath Dr.
Steinheil.
Mit Abbildungen auf Tab.
VII.
Steinheil, über Reichenbach's Distanzmesser.
Die Aufgabe „durch den Reichenbach'schen
Distanzmesser die Horizontalprojection des Abstandes zweier Terrainpunkte zu
finden“, scheint nach dem Aufsatze des Hrn. Professor Decher im polytechn. Journal, 1850,
Bd. CXVI S. 29 auf erhebliche Complication zu führen. Es werden, nachdem schon die
Berechnung der Theilung der Latte ziemlich viel Arbeit macht, zwei verschiedene
Hülfstafeln, die eine für Elevation, die andere für Depression erforderlich. Beide
haben doppelten Eingang, was bekanntlich immer auf unbequeme Interpolation führt.
Dadurch verliert das Instrument in der Anwendung – um mit Bessel zu reden – so sehr den edeln Charakter der
Einfachheit, daß wenn sich diese Schwierigkeiten nicht beseitigen ließen, es sehr
zweifelhaft bliebe, ob nicht andern Messungsmitteln der Vorzug gebührt. Denn unter
den vielen Messungsmitteln welche bestehen ist immer dasjenige das praktische, was
mit dem geringsten Aufwand von Mühe und Zeit die verlangte Genauigkeit gibt, und
diese Rücksicht muß immer maßgebend seyn bei der Wahl des Meßapparates.
Indessen gestattet Reichenbach's Instrument in der That eine viel einfachere Behandlung,
die weder Hülfstafeln, noch eine eigene Berechnung der Distanzlatte voraussetzt und
dennoch dieselbe Genauigkeit gibt. Da ich mich dieser Methode schon vor mehr als 25
Jahren vielfach bediente und sie bequem fand, so veranlaßt mich die Hoffnung, daß es
auch andern Besitzern dieses Instruments eben so gehen werde, zu deren nachfolgenden
Bekanntmachung.
Es bezeichne
a den kleinsten Abstand der Mitte der Distanzlatte von
dem Mittelpunkt des Objectives,
α die Vereinigungsweite der von a kommenden Lichtstrahlen,
r den Abstand der beiden horizontalen Ocularfäden auf
der Distanzlatte gemessen.
Bezeichnen wir diese Größen für eine andere Entfernung der Distanzlatte mit einem
Striche, also mit
a'
α'
r', und nennen wir
ρ den kleinsten Abstand der Ocularfäden in derselben
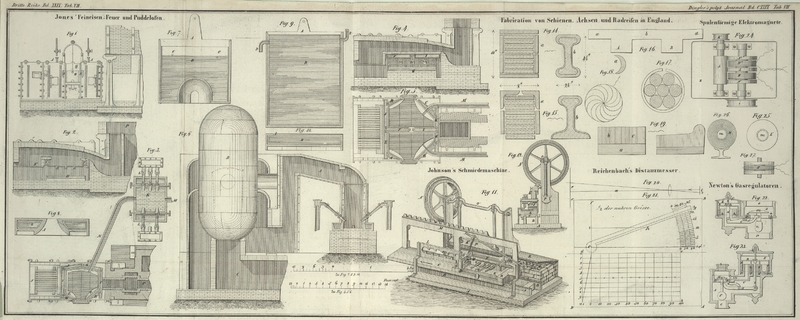
Längeneinheit gemessen, so hat man, wie aus Fig. 20 zu ersehen:
a : r = α : ρ
a' : r' = α' : ρ
denn es wird für die zweite Stellung der Distanzlatte wohl
erforderlich, die Fäden mit dem Oculare von α nach α' zu verstellen,
aber der Abstand der Fäden ρ ändert sich nicht. Man hat sonach:
r = aρ/α
r' = a'ρ/α'
(1)
Nun ist aber die Relation zwischen Abstand, Brennweite und Vereinigungsweite für
Strahlen die der Achse sehr nahe liegen, und für unendlich kleine Dicke der
Objectivlinse, wenn wir Euler's Bezeichnungen beibehalten, bekanntlich:
1/a + 1/α = 1/p
und eben so
1/a' + 1/α' = 1/p,
woraus folgt
1/α =
1/p – 1/a 1/α' = 1/p – 1/a'
(2)
Diese Werthe in (1) gesetzt, geben
r = ρ (a – p)/p
r' = ρ (a' –
p)/p
woraus sich das Verhältniß der Ablesungen an der Distanzlatte
zu den Abständen der Latte
r/r' = (a – p)/(a' – p)
(3)
findet.
Wir sehen hieraus, daß die Theilung der Distanzlatte für alle Abstände der Latte
letzteren proportional ist, wenn die Abstände der Latte
von demjenigen Punkte aus gezählt werden, der um p, d.
i. um die Brennweite des Objectives, vor dem Objectiv liegt.
Aus (3) folgt unmittelbar:
a' – p = r'/r (a – p)
(4)
Soll nun auf 1000 Fuß Abstand die Theilung der Distanzlatte 10 Fuß umfassen, so
wird
(a – p)
= 1000
r
= 10,
daher
(a' –
p)
= (100) r'
(5)
d.h. die Differenz der zwei Ablesungen an der Distanzlatte
100mal genommen, ist gleich der Entfernung der Latte von dem Punkte, der um die
Brennweite vor dem Objectiv liegt. Die Distanzlatte wird sonach direct in denjenigen
Längenmaaßeinheiten getheilt, in welchen man die Distanzen messen will, und jede
Latte gilt für jedes Instrument, wenn sein Fädenabstand berichtigt ist.
Soll nun aber der Abstand nicht von dem Objective, sondern von einem bestimmten Punkt
in der Figur auf dem Meßtisch gezählt werden, wofür wir den Durchschnitt der
Drehungsachse mit der optischen Achse substituiren können, da sich dieser Punkt
immer senkrecht über den entsprechenden in der Figur bringen läßt, so nimmt der
Ausdruck (5), wenn wir mit u obigen Abstand bezeichnen,
die Form an
a' + u = (100) r' + p + u.
Allein (p + u) ist eine
constante Größe, die nur ein für allemal für jedes Instrument abzumessen ist und
dann jeder Ablesung im Kopfe beigefügt werden kann. Setzen wir
p + u = C
so wird der Abstand des Mittelpunktes der Distanzlatte von der
Drehungsachse des Instrumentes:
a' + u = (100)
r' + C
(6)
Wenn sonach der eine Faden auf den Nullpunkt der Scala eingestellt wird, zeigt der
andere Faden auf r', und diese Ablesung 100mal genommen
und um C vergrößert, gibt den verlangten Abstand in
denjenigen Einheiten, in welchen die Latte getheilt ist.
Es versteht sich von selbst, daß man zur Berichtigung des Fädenabstandes etwa 100
Lattentheilungslängen abmißt, die Brennweite des Objectives zulegt, in diesem Punkte
das Objectiv, im andern Endpunkt die Latte aufstellt und nun einen oder auch beide
Fadenschuber durch die Schrauben verstellt, bis die Fäden zugleich, der eine auf den
obersten, der andere auf den untersten Theilstrich der Latte treffen.
Nennt man die Horizontalprojection des Abstandes a' + u π, die Neigung der Absehnslinie des oberen
Oculares nach dem Nullpunkt gegen den Horizont i,
so wird
π = Cos i (100 r' + C)
(7)
Der Winkel, den die beiden Absehnslinien mit einander bilden, ist für 1000 Fuß
Abstand unter obigen Annahmen 34,4 Minuten. Für diesen Winkel beträgt der
Unterschied zwischen Sinus und Tangens 4 Einheiten der 5ten Decimalstelle. Da man aber mit dem
Distanzmesser nur circa 1/500, also nicht einmal eine
Einheit der 4ten Decimalstelle richtig bekömmt, so ist es in Bezug auf die normale
Stellung der Distanzlatte zur Absehnslinie gleichgültig, in welchen Zwischenpunkt
zwischen beide Absehnslinien der rechte Winkel verlegt wird. Vernachlässigungen
derselben Ordnung sind auch schon begangen in (2) und sie finden sich eben so in den
Entwickelungen des Hrn. Prof. Decher.
Demzufolge können wir den Nullpunkt der Distanzlatte in ihre
Mitte verlegen. Wir nehmen an, daß diese Höhe von 5 Fuß gleich sey der Höhe
der Drehungsachse des Instrumentes über dem Fußboden.Sollte man in einzelnen Fällen genöthigt seyn, bei der Aufstellung des
Instrumentes hievon abzugehen, so wird durch Vergleichung der Latte mit der
Höhe in welcher die Achse aufgestellt ist, der Strich der Theilung bekannt,
der gleiche Höhe mit der Achse hat und auf diesen Strich wird dann der obere
Ocular-Faden eingestellt, wenn der Höhenkreis zur Bestimmung der
Neigung i abgelesen werden soll.
Sind nun Meßtisch und Distanzlatte in derselben Horizontalebene aufgestellt, so muß,
wenn das obere Ocular auf den Nullpunkt zeigt, auch der Höhenkreis Null zeigen, oder
es wird dessen Inder auf diesen Punkt gebracht. Nun gibt der Höhenkreis unmittelbar
die Neigung der Absehnslinie oder den Winkel ± i
auch in anderem Terrain.
Für größere Abstände als 500 Fuß wollen wir den Nullpunkt der Theilung in den
obersten Theilstrich der Distanzlatte verlegen und die zweite Hälfte der Theilung der
Distanzlatte von der Mitte aus bis zum Fußpunkte zählen.
Das obere Ocular auf den mittlern Nullstrich der Latte eingestellt, gibt daher immer
die Neigung i; aber für Entfernungen die größer als 500
Fuß sind, wird nach der Bestimmung von i der untere
Ocularfaden auf den obersten Theilstrich der Latte gebracht und am obern Oculare die
Ablesung r' gemacht, die jetzt stets in die untere
Hälfte der Latte fällt.
Die Absehnslinie des Visirs der Latte ist in der Mitte im Nullstrich normal auf die
Ebene der Latte gestellt. Daher bleibt bei allen Neigungen des Terrains die Normale
der Mitte der Lattenebene senkrecht zur Drehungsachse des Instrumentes.
Um die Distanzlatte in der Verticalebene zu erhalten die zugleich durch das Objectiv
geht, dient in der Regel ein Senkel, der oben an der Latte befestigt ist. Diesen
Senkel befestige ich an dem mittlern Nullstrich der Latte in einem schmalen
Längendurchschnitt und benutze ihn zugleich senkrecht auf die oben genannte Ebene
zum Ablothen des Nullstriches, indem die Latte so gestellt
wird, daß das Loth auf den Punkt trifft, dessen Horizontalprojection bestimmt
werden soll. Das Loth reicht nicht bis zum Fußpunkt der Latte, sondern bis
zum Theilstrich 9 Fuß von oben. Wird nun die Latte geneigt, so kömmt der Nullstrich
näher zum Boden, um wieviel, dieß zeigt sehr nahe die Spitze des Senkels an der
Lattentheilung. Um eben so viel wird über dem Nullstrich eingestellt vor Ablesung
des Höhenkreises. Uebrigens beträgt diese Correction bei einer Neigung von
20° (der größten welche der Distanzmesser aufwärts zu messen gestattet) und
bei 50 Fuß Abstand der Latte, nur 1/391 der reducirten Entfernung, und ist somit nur
in ganz ungewöhnlichen Fällen in Anwendung zu bringen.
Es erübrigt jetzt nur noch, den gemessenen Abstand des mittlern Nullstriches der
Latte mit der Neigung i auf den Horizont zu reduciren.
Allein da man diese Linie in die Figur auf dem Meßtisch eintragen soll und folglich
die entsprechende Zirkelöffnung benöthiget, ist es kürzer auch die Reduction gleich
graphisch auszuführen.
Dieß kann geschehen mit Hülfe eines auf Messing getheilten Gradbogens von 25°
Umfang, der dem gewöhnlichen 2500theiligen und 5000theiligen Transversalmaaßstab
beigefügt ist.
Es sey Fig.
21, A, B, C, D ein Messingblech, auf welchem der
Transversalmaaßstab abde getheilt ist. Um c drehe ein abgeschrägtes Lineal, dessen abgeschrägte
geradlinige Kante genau nach dem Centrum c geht und auf
der Ebene des Bleches aufliegt. Der Drehungspunkt c sey
zum Einsetzen der
Zirkelspitze conisch vertieft. Die Kreistheilung sey von Grad zu Grad durch
Transversalen von 20' zu 20' getheilt. Senkrecht auf cc' ist cf errichtet.
Beim Gebrauche wird erst die abgelesene corrigirte Entfernung a' + u (6) mit dem Zirkel am
Transversalmaaßstab abde entnommen, dann das
Lineal cg auf die am Höhenkreis abgelesene Neigung
i eingestellt. Hierauf wird der eine Schenkel des
Zirkels in c eingesetzt und der andere an die Kante des
Lineals cg gebracht. Dieser letzte Punkt sey h. Nun wird der Zirkel um h
gedreht und seine Oeffnung vermindert bis die Spitze, die früher auf c stand, die Gerade df
tangirt. Die Oeffnung hi des Zirkels ist nun π oder die verlangte Horizontalprojection des
Abstandes des Senkelpunktes der Latte von dem Fußpunkte des Durchschnitts der
Drehungsachse des Instrumentes mit der optischen Achse.
München, den 30. August 1853.
Tafeln