| Titel: | Versuche über die Luftreibung an den Röhrenwänden einer Windleitung; von P. Rittinger, k. k. Sectionsrath, |
| Fundstelle: | Band 143, Jahrgang 1857, Nr. XXXV., S. 162 |
| Download: | XML |
XXXV.
Versuche über die Luftreibung an den Röhrenwänden
einer Windleitung; von P.
Rittinger, k. k. Sectionsrath,
Aus der österreichischen Zeitschrift für Berg- und
Hüttenwesen, 1856, Nr. 51.
Mit Abbildungen auf Tab.
III.
Rittinger, Versuche über die Luftreibung an den Röhrenwänden einer
Windleitung.
Der Effect der in einer Windleitung sich bewegenden Luft wird durch drei Größen
bestimmt:
1) durch ihre Pressung oder durch die Höhe b, welche ein
senkrecht in die Seitenwand der Windleitung eingestelltes Wassermanometer
angibt;
2) durch ihre Geschwindigkeit U, und
3) durch die Windmenge M, welche per 1 Secunde durch jeden Querschnitt der Windleitung
hindurchstreicht.
Fast bei allen bisherigen Betrachtungen in der Aerodynamik wird bei Bestimmung des
Effectes der in Röhren sich bewegenden Luft von der
Geschwindigkeit U abgesehen, was aber nicht immer
zulässig ist; denn es kann in manchen Fällen der größere Theil des Effectes der Luft
in ihrer Geschwindigkeit begründet seyn, die Pressung dagegen auf denselben nur
einen geringen Einfluß nehmen. Dieß ist z.B. der Fall beim Austritte der Luft aus
einer Düsenmündung, wo die Luft die atmosphärische Pressung annimmt, ja sogar etwas
unter dieselbe herabsinkt, während ihre Geschwindigkeit vorherrscht und vorzugsweise
ihren Effect bestimmt; oder bei einer engen Windleitung, wenn durch dieselbe die
Luft mit bedeutender Geschwindigkeit hindurchströmt.
Es gibt ein sehr einfaches Mittel, die Geschwindigkeit der
Luft mit ihrer Pressung zugleich abzunehmen und in
Rechnung zu bringen; man
wendet nämlich bei der Beobachtung des Manometerstandes einen einfachen Hülfsapparat
an, welcher aus einem um 90 Grade gebogenen Röhrenstücke aus Eisenblech besteht, und
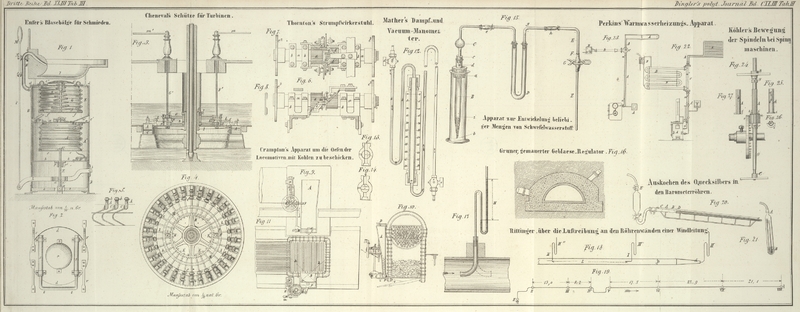
über welches ein kurzer Holzcylinder geschoben ist, wie dieß Fig. 17 versinnlicht.
Dieses Hülfsröhrchen steckt man nun in die Oeffnung, an
welcher man den Manometerstand zu beobachten beabsichtigt, und zwar so, daß der
horizontale Schenkel desselben gerade gegen den Windstrom
gerichtet ist, und steckt sodann in dessen verticalen Schenkel das
Wassermanometer ein.
Auf den Rand der letzteren wird nun nicht bloß die Pressung der Luft, sondern auch ihre Geschwindigkeit einwirken, und man kann sehr leicht von der Größe des
letzteren Einflusses sich überzeugen, wenn man das Hülfsröhrchen um 180°
wendet, so daß der horizontale Schenkel in der Richtung des
Windstromes zu liegen kommt. War in ersterer Stellung die Wassersäulenhöhe
= H, so wird sie in der zweiten Stellung = h seyn, und es ist
H – h = s
ein aus der Geschwindigkeit herrührender Zuwachs, da die Höhe
h bloß der Pressung allein ihren Ursprung verdankt.
Statt daher wie gewöhnlich den Effect der durch Röhren durchströmenden Luft
durch
E = M h γ
auszudrücken (unter γ das
Gewicht einer kubischen Einheit Wasser verstanden), soll derselbe vielmehr durch
(1) . . . . E = M H γ
dargestellt werden.
Beobachtet man auf die angedeutete Weise den Manometerstand an mehreren Punkten einer
längeren Windleitung, deren Röhren durchaus einen gleichen
Durchmesser
D besitzen, so wird man die Höhe H um so kleiner finden, je mehr man sich den Düsen nähert. Diese Abnahme
der effectiven Manometerhöhe
H hat bekanntlich ihren Grund in der Reibung der Luft an den Röhrenwänden. Bezeichnet man die
an zwei beliebigen Punkten I und II einer Windleitung (Fig. 18) beobachteten
effectiven Manometerstände mit H' und H'', so ist der Effect
in
II
E''
=
M H'' γ,
und
in I
E'
=
M
H' γ;
daher der Effectverlust in Folge der Luftreibung
(2) . . . . e = E'' – E' = M (H'' – H') M γ.
Dieser Effectverlust wird also durch die Größe des Unterschiedes zwischen den effectiven Manometerhöhen
H'' und H' bestimmt.
Uebereinstimmend mit den Erfahrungen bei der Bewegung des Wassers in Röhren steht
dieser Unterschied H'' – H'
a) mit dem Abstande L
zwischen den beiden Beobachtungspunkten I und II im geraden Verhältnisse;
b) mit dem Durchmesser D der
Röhren im verkehrten Verhältnisse, endlich
c) hat auch die Geschwindigkeit U der Luft einen wesentlichen Einfluß auf den Effectverlust, indem
letzterer im geraden quadratischen Verhältnisse von U
zunimmt.
Bezeichnet α einen Erfahrungscoefficienten, so
kann man daher setzen:
(3) . . . . H'' – H' = α L/D U²
Die absoluten Pressungshöhen h'' und h' haben auf den Werth von e
keinen wesentlichen Einfluß.
Die Geschwindigkeit U läßt sich aber wegen
M = D²π/4 U
ausdrücken durch:
U = 4M/D²π
Die Windmenge M hängt wieder von der Zahl N der offenen Düsen, vom Durchmesser d und von der Ausflußgeschwindigkeit c ab, und man hat dafür den Ausdruck:
M = kN d²π/4 c,
wenn k den Ausflußcoefficienten
bedeutet. Es ist daher auch:
U = 4/D²π . kN d²π/4 c
U = d²/D² kNc
Bezeichnet H die effective Manometerhöhe vor den Düsen
und δ das Gewicht einer kub. Einheit Luft von
atmosphärischer Dichte, so hat man
Textabbildung Bd. 143, S. 164
es ist daher mit Benützung dieses Werthes für c
U² = d⁴/D⁴ k²N² 2 gH δ/γ, also nach Formel (3)
H'' – H' = αk² 2 g
δ/γ d⁴/D⁵ N²LH.
Setzt man das aus lauter constanten Factoren bestehende Product
(4) . . . . αk² 2 g δ/γ = ζ,
so kann man den Unterschied zwischen den effectiven
Manometerhöhen auch darstellen durch:
(5) . . . . H'' – H' = ζ d⁴/D⁵ N²LH
d'Aubuisson fand aus vielen von ihm abgeführten
Versuchen, wobei aber nicht die effectiven Höhen H'', H'
und H, sondern die Pressungshöhen h'', h' und h beobachtet und in Rechnung
gebracht wurden:
ζ = 0,0238.
Ich stellte es mir zur Aufgabe, die Richtigkeit dieses Luftreibungscoefficienten bei Gelegenheit anderer Gebläse-Versuche,
die ich im k. k. Gußwerke bei Maria-Zell im laufenden Jahre abführte, mit
Berücksichtigung der effectiven Manometerhöhen durch
eigene Versuche zu prüfen.
Die dabei angewendete Windleitung ist im Ganzen 103 Meter (327 Fuß) lang und 0,210
Meter (8 Zoll) weit; sie besteht aus genietetem Eisenblech mit gußeisernen Kränzen
und ist eigentlich zur Dampfheizung für ein längeres Local bestimmt, wurde daher
bloß gelegentlich zur Windleitung verwendet. Die ganze Windleitung ist in Fig. 19
übersichtlich dargestellt; man sieht, daß dieselbe aus zwei geraden Partien von
bedeutender Länge besteht, zwischen welchen ein viermal gebogenes Stück
eingeschaltet ist. Um mit verschiedenen Windmengen und bei verschiedenen
Geschwindigkeiten zu experimentiren, wurde die äußerste Mündung bei VIII. nach
einander mit gußeisernen Platten geschlossen, an welche je ein düsenförmiges 4 Zoll
langes Mundstück von 0,039, 0,066 und 0,105 Meter, oder von 1 1/2, 2 1/2 und 4 Zoll
Durchmesser angegossen war. Außerdem wurde auch ohne jeden Düsenansatz durch die
8zöllige Röhrenmündung unmittelbar geblasen. Den durch die Windleitung streichenden
gepreßten Wind lieferte ein Ventilator, dessen Anwendung
den Vortheil mit sich brachte, daß die Manometerstände nur sehr geringe Schwankungen
wahrnehmen ließen. Die Manometer wurden übrigens an den in Fig. 19 mit römischen
Zahlen bezeichneten Punkten in der oben beschriebenen Weise und an jedem Punkte
doppelt beobachtet, indem der horizontale Schenkel des Hülfsröhrchens das einemal
gegen die Windrichtung, das anderemal entgegengesetzt, nämlich nach der Windrichtung
gestellt wurde.
Für die einzelnen geraden Rohrstücke sind die Beobachtungsdaten im metrischen Maaße,
nach den Röhrenlängen und Düsendurchmessern gruppirt, in nachstehender Tabelle zusammengestellt:
Resultate der Versuche zur Bestimmung des
Widerstandscoefficienten bei der Bewegung der Luft durch lange
Röhrenleitungen.
Textabbildung Bd. 143, S. 166
Versuchs-Nummer;
Bezeichnung; Entfernung; der beiden Beobachtungspunkte; Nummer;
Düsendurchmesser; Effektive Manometerhöhe; am 1.
Manometer; am 2. Manometer; an der Düse; Berechneter Widerstandscoefficient;
Meter; Zahl
In dieser Tabelle erscheinen die aus den Daten sich ergebenden Werthe des
Coefficienten ζ mit Benützung der Formel (5)
berechnet; man hat nämlich:
(6) . . . . ζ = (H'' – H')D⁵/(N²Ld⁴H)
Für die abgeführten Versuche ist die Düsenzahl N = 1 und
der Röhrendurchmesser D = 0,210 zu setzen.
Aus den Versuchen 1, 4, 7, 10 und 13, welche bei ganz offener
Röhrenmündung abgeführt wurden, folgt im Mittel:
ζ₀ = 0,0205
und nach der Methode der kleinsten Quadrate:
ζ₀ = 0,0202.
Die übrigen Versuche, mit Ausnahme von 6 und 9, welche wegen zu abweichender
Resultate nicht berücksichtigt wurden, geben im Mittel den Werth:
ζ = 0,0303
und nach der Methode der kleinsten Quadrate fast dasselbe,
nämlich:
ζ = 0,0306.
Der Grund, warum die beiden Werthe von ζ₀
und ζ von einander abweichen, liegt darin, daß
bei ganz offener Windleitung keine Contraction wie bei
Düsen stattfindet; der Contractionscoefficient k² muß daher aus dem berechneten Werthe für ζ₀ durch Division ausgeschieden werden,
und es ist also:
ζ = ζ₀/k², daher
k = √(ζ/ζ) = √(0,0202/0,0306) = 0,81,
welcher Werth mit dem für conische Ausflußrohren (Düsen)
gefundenen Ausflußcoefficienten (= 0,85) sehr nahe übereinstimmt.
Es ist daher der Röhrenwiderstands-Coefficient für jenen Fall, wenn durch Düsen geblasen wird, sehr nahe:
(7) . . . . ζ = 0,03,
also etwas größer, als derselbe von d'Aubuisson bestimmt wurde.
Man hat demnach:
(8) . . . . H'' – H' = 0,03 d⁴/D⁵ N²LH.
Denkt man sich das Manometer, welches die Höhe H'
anzeigt, bis an die Düse gerückt, so muß
H' = H
gesetzt werden, und es gibt H''
– H den Verlust an effectiver Höhe für die ganze
Länge L der Windleitung vom Beobachtungspunkte für H'' angefangen, bis zur Düsenmündung.
Man hat dann:
H'' – H = 0,03 d⁴/D⁵ N²LH, also
(9) . . . . H'' = (1 + 0,03 d⁴/D⁵ N²L) H.
Mit Hülfe dieser Formel läßt sich aus der gegebenen effectiven Manometerhöhe H in oder vor den Düsen die effective Manometerhöhe H'' für einen beliebigen Abstand L leicht berechnen. Ist z.B. der Durchmesser zweier Hohofendüsen
d = 30'' = 0,066 Meter,
und jener der geraden Windleitung
D = 10'' = 0,263 Meter,
soll ferner die effective Manometerhöhe an den Düsen
H = 24'' Quecksilber = 0,715 Meter Wassersäule
betragen, so wird die effective Manometerhöhe in einem
Abstande L = 100 Meter von den Düsenmündungen sich
ergeben aus:
H = (1 + 0,03 (0,066)⁴/(0,263)⁵ 2²
. 100) 0,715
= 1,18 . 0,715 = 0,844 Meter.
Die effective Manometerhöhe H'' muß also in 100 Meter
Distanz um 18 Proc. größer gehalten werden, als vor den Düsen.
Tritt die Luft aus der Windleitung unmittelbar, ohne Anwendung
von Düsen, heraus, so muß statt des Coefficienten ζ = 0,03 der Coefficient ζ =
0,02 in Rechnung genommen werden.
Die abgeführten Versuche liefern auch einige Anhaltspunkte zur Schätzung des
Verlustes an effectiver Druckhöhe in Folge von Biegungen der Windleitung. Die vier
Kniee, welche ungefähr im ersten Drittel der Leitung
vorkommen, waren nach einem mittleren Halbmesser = 8 Zoll = 0,21 Meter, also
ziemlich stark gekrümmt. Außer dem Verluste an effectiver Höhe, welcher aus der
Länge l = 10 Meter des ganzen Röhrenstückes zwischen IV
und V entspringt, hat der Verlust betragen: bei einer Luftgeschwindigkeit
von
15,6
Meter
für
1 Knie
0,011
Meter
„
10,4
„
„
„
0,005
„
„
5,9
„
„
„
0,002
„
Als besondere in diesen Versuchen gemachte Wahrnehmung
möge hier erwähnt werden:
1. Daß der Unterschied H – h = s, d. i. die in der Geschwindigkeit der Luft begründete
Zunahme an Manometerhöhe bei jedem Versuche in der ganzen Erstreckung der
Windleitung sich ziemlich gleich geblieben ist, woraus hervorgeht, daß die
Geschwindigkeit U in allen Querschnitten der Windleitung
dieselbe war. Dadurch wird die von d'Aubuisson
aufgestellte Behauptung widerlegt, daß die Geschwindigkeit in der Richtung der
Bewegung allmählich zunimmt.
2. Beim Blasen durch die kleinste Düse von 1 1/2 Zoll im Durchmesser unter der
Pressung H = 0,35 Meter = 13 1/3 Zoll war keine Abnahme
an effectiver Manometerhöhe mehr bemerkbar.
3. Die Manometerhöhen waren nur bei Anwendung größerer Düsen, also bei größerer
Geschwindigkeit stationär, bei kleineren Düsen fand ein merkliches Schwanken statt,
welches beim gänzlichen Schluß ins Schwingen überging. Der Grund dieser Erscheinung
liegt in der Wirkungsweise der windliefernden Maschine, nämlich im Ventilator.
Tafeln