| Titel: | Die Thomas'sche Rechenmaschine; von Prof. F. Reuleaux in Zürich. |
| Fundstelle: | Band 165, Jahrgang 1862, Nr. LXXXIII., S. 334 |
| Download: | XML |
LXXXIII.
Die Thomas'sche
Rechenmaschine; von Prof. F. Reuleaux in Zürich.
Aus dem Civilingenieur, 1862, Bd. VIII S.
181.
Mit Abbildungen auf Tab.
V.
Reuleaux, über die Thomas'sche Rechenmaschine.
Das Maschinenwesen hat einen Hauptantheil an der großartigen culturhistorischen
Aufgabe, die Menschheit von den rohen, beschwerlichen und namentlich den
geisttödtenden Arbeiten frei zu machen; und nicht bloß heute in Amerika, sondern
längst im großen Ganzen müssen die Maschinen als Mittel bezeichnet werden, die
Sclaverei aus der Welt zu verbannen. Ein eigenes Gefühl überkommt uns, wenn wir
letzteres heute sowohl als edles Ziel menschlichen Strebens hingestellt sehen, als
auch dasselbe unwillkürlich überall zu Tage tretend finden, und damit vergleichen,
was die Alten von derselben Frage hielten. Ironisch belächelt Aristoteles in seiner „Politik“ (I, Cap. 2, 5) die
Schwärmer, welche gegen
die Sclaverei eingenommen sind. „Freilich“, sagt er,
„wenn jedes Werkzeug auf's Geheiß, oder gar dasselbe im voraus
errathend sein Werk verrichten könnte, wie das die Statuen des Dädalos, sagt
man, thaten, oder die Dreifüße des Hephästos, von denen der Dichter singt, daß
sie „ganz von selbst in die Versammlung der Götter rollten“
– wenn so auch die Weberschiffe selbst webten und die Citherschlägel die
Cither schlügen, dann freilich brauchten die Baumeister weder Handlanger, noch
die Herren Sclaven.“ Solchem gegenüber muß eine Zeit hochbedeutend
erscheinen, in welcher das zu erfüllen begonnen worden ist, was die Weisesten der
Weisen ehemals für völlig unmöglich und märchenhaft hielten. Nun, unter die
Sclavenarbeiten, kaum besser als die „Handlangerei“ beim
Baumeister des Aristoteles, gehört die geistige Handlangerei großer
Zahlenrechnungen, wie sie der Maschinen-, Bau-, Berg- und
Militäringenieur, der Physiker, der Astronom und der Zahlenmathematiker oder
Arithmetiker, der Steuer- und Finanzbeamte u.a.m. viele Stunden, Tage,
Wochen, Monate lang auszuführen haben. Fast keine geistige Erschlaffung ist größer
als diejenige nach tagelang fortgesetzter Beschäftigung mit dem Abstractum der
Zahlen, namentlich in höheren Rechnungsarten, und bekannt ist es, daß es bis jetzt
nicht menschenmöglich gewesen ist, Logarithmentafeln fehlerfrei zu rechnen, indem
der menschliche Geist sich entschieden zu sträuben scheint, in die unbeugsame Maschinenmäßigkeit einzutreten, welche dafür gefordert
wird. Es muß deshalb eine Erfindung mit Freuden begrüßt werden, welche die Sclaverei
des Rechnens zu brechen gekommen ist, und es ist eine solche, auf welche ich hier
die sonderbarer Weise noch nicht darauf geführte Aufmerksamkeit der deutschen
Rechner lenken möchte.
RechenmaschinenVielleicht ist es nöthig, hinzuzufügen; „nicht
Rechnenmaschine“; denn es scheint fast, als wolle es diesem
widrigen Sprachfehler, der auch in „Zeichnenpapier“
etc. vorkommt, und durch Büchertitel, Zeitungsanzeigen, Schulprogramme und
Bücher geschützt wird, gelingen, sich zum Nachtheil des Sprachgefühls
einzuschwärzen. Wer für „Rechnenbuch“,
„Zeichnenzimmer“ auftreten will, muß auch
„Schwimmenschule“,
„Fechtenboden“, „essenbar“,
sagen. Verwechslung ist nicht zu fürchten, und würde auch den Fehler nie
entschuldigen, welchen zu vermeiden man in der Schweiz die nicht nur
steifen, sondern auch unrichtigen Formen:
„Zeichnungspapier“,
„Rechnungsstunde“ eingeführt hat. Nach Abwerfung
der Infinitiv-Endung bleibt vom ursprünglichen Zeitwort
„rechenen“ der zum Zusammensetzen geeignete Stamm
übrig, worüber jedes gute linguistische Werk belehrt. hat man schon früher zu machen versucht, indem die regelmäßige Wiederkehr
gleicher Vorgänge dazu auffordern mußte. Ja von dem Rechnen mit
„Steinchen“ bei Griechen (Ψῆφος , Ψηφίζω) und Römern (calculos ponere, calculare) bis heute weist die
Geschichte der Zahlen eine ununterbrochene Reihe von Versuchen auf, die
Gesetzmäßigkeit der Zahlen zu benutzen, um sie mechanisch hervorzubringen. Vieles davon ist
verloren gegangen, die Logarithmen wurden beim Suchen nach dem Recheninstrument
gefunden. In Pascal's berühmt gewordener, aber nicht
praktischer Rechenmaschine finden sich die ersten Anfänge zu dem heute mit Glück
verfolgten Wege. Nach ihm versuchte sich auch Leibnitz
ohne eigentlichen Erfolg an der Aufgabe. Von da ab folgen sich rasch und rascher die
fast immer scheiternden oder aufgegebenen Versuche, deren gesammter Geldaufwand sich
nach Millionen berechnet. 1821 begann Babbage seine 1833
fertig gewordene Rechenmaschine, welche 425000 Franken kostete, die aber dennoch als
nicht praktisch befunden von ihm nicht weiter ausgebildet wurde. Doch war sie im
Grunde das Vorbild der endlich mit Erfolg ausgeführten Scheutz'schen oder schwedischen Rechenmaschine,
welche im abgelaufenen Jahrzehend fertig wurde und im polytechn. Journal Bd. CLVI S.
241 und 321 beschrieben ist.
Diese Maschine, obgleich gänzlich verschieden in Zweck und Mitteln von der unten zu
besprechenden, verdient hier eines kleinen Verweilens, da sie weder im allgemeinen
genug gewürdigt, noch auch ihrem Zweck und Erfolg nach genug bekannt scheint. Die
Maschine von Babbage und darnach die Scheutz'sche hat nicht den Zweck, beliebige Rechnungen zu
vollbringen, sondern dient einzig und allein zur Herstellung
von Tabellen, in welchen gesuchte Werthe von Formeln für eine geordnete
Anzahl von Werthen der gegebenen Größen zusammengestellt sind, und beruht darauf,
daß bei solchen Zahlenfolgen sich durch fortgesetztes Bilden der Unterschiede
aufeinanderfolgender Werthe schließlich Zahlenreihen von lauter gleichen Gliedern
ergeben. So z.B. finden sich, wenn man die Folge der Quadrate
der natürlichen Zahlenreihe in der genannten Weise behandelt, die
nachstehenden Zahlen:
0
1
4
9
16
25
36
49
1
3
5
7
9
11
13
2
2
2
2
2
2
Also schon die dritte Differenzfolge besteht aus gleichen Gliedern. Addirt man nun
das erste Glied der zweiten Reihe zu einem der dritten, so erhält man das zweite
Glied der zweiten Reihe, durch fernere Addition der constanten Differenz das dritte
u.s.f. Verfährt man darauf von der zweiten zur ersten Reihe ähnlich, so ergiebt sich
– die letzte Differenzenreihe von constanten Gliedern, und die ersten Glieder
der übrigen Reihen als bekannt vorausgesetzt – die ganze unendliche Folge der
Quadrate der natürlichen Zahlenreihe durch fortgesetzte
Addition, welche maschinell nahe liegt. Auf diese Grundlage hin, welcher es
zu statten kommt, daß sehr viele Zahlenfolgen, u.a. auch die Logarithmen nicht viele Differenzreihen bis
zu derjenigen von gleichen Gliedern (welcher Differenzen = 0 entsprechen) besitzen,
gründete Babbage seine Maschine. Scheutz (Vater und Sohn) nahmen dieselbe auf, wandten darauf ihren ganzen
Fleiß und zudem ihr Vermögen und kamen schließlich unter der endlich erlangten
Beihülfe des Staates zu einem vortrefflichen Ergebniß.Von diesem erwähnt Régnier in seiner
„Histoire des
nombres“ auffallender Weise Nichts oder nur
Negatives.
Scheutz gieng davon aus, daß
1) die Berechnung logarithmischer und astronomischer Tafeln die Maschine wichtig
mache, und daß
2) mit dem bloßen richtig rechnen nicht genug geschehen
sey, indem der Druck solcher Tafeln durch das Setzen
immer wieder Fehler bekomme.
Die Scheutz'sche Maschine wurde deßhalb darauf
eingerichtet, daß sie Tabellen obiger Art zu rechnen und
zu stereotypiren und zwar mit allen übrigen
Druckerfordernissen, als Seitenzahl, Strichen etc., zu versehen im Stande ist. Dieß
alles ist den braven ausdauernden Erfindern – darf man gewiß sagen –
nach jahrelangen Mühen gelungen, und zwar vollkommen gelungen. Die Scheutz'sche Maschine war, obwohl wenig gesehen, eine der
glänzendsten Zierden der letzten Pariser Ausstellung. Eine auf ihr gerechnete und
stereotypirte vollkommen fehlerfreie Logarithmentafel ist von den Beschützern der
bescheidenen Nordländer an viele Orte hingesandt worden. Schließlich wurde die
Maschine von dem Smithonian-Institute
angekauft, um von Amerika aus die Verbreitung ganz wohlfeiler Zahlentafeln irgend
welcher Art, vor allem Logarithmentafeln, zu bewirken.
Ungefähr gleichzeitig mit der vortrefflichen, freilich sehr verwickelten und theueren
Scheutz'schen Rechenmaschine, welche, wie gesagt, nur
für besondere Zwecke, nicht aber für das Ausführen einzelner gewöhnlichen Rechnungen
bestimmt ist, hat sich in Frankreich die Maschine des Elsässers Thomas ausgebildet; sie wurde 1820Siehe: Bulletin de la Société
d'Encouragement, p. 455, pl. 232. patentirt, hat sich, von einem zweckmäßigen Grundgedanken ausgehend, 30
Jahre hindurch neben sehr zahlreichen Concurrenzmaschinen, die alle nach und nach
unterlegen sind, behauptet, und ist schließlich zu einer Vollkommenheit gebracht
worden, welche ihr einen Platz unter den mathematischen Instrumenten der höchsten
Gattung erworben hat, ja welche sie binnem kurzem zu einem für den ausführenden Mathematiker ganz unentbehrlichen
Hilfsmittel machen wird.
Sie ist eine Maschine, mit welcher man, um es mit einem schlichten Wort zu sagen, die
4 Species ausführen, aber ungemein rasch ausführen kann, und diese schlichte Kunst
ist von einem solchen Vortheil, von einer solchen Bedeutung für das numerische
Zahlenwesen, wie wohl bisher noch wenige in dieses Gebiet fallende praktische
Erfindungen gewesen sind. In Frankreich hat sich der „Arithmometer“ schon ziemlich stark
verbreitet; merkwürdiger Weise kennt ihn bis jetzt Deutschland kaum dem Namen nach.
An der hiesigen polytechnischen Schule (welche zwei Exemplare anschaffte) arbeiten
wir seit 1 1/2 Jahren fortwährend damit, und hoffentlich wird der vorliegende
Aufsatz dazu beitragen, das fast unschätzbare Instrument auch in Deutschland nach
allen Seiten hin zur Aufnahme zu bringen.
Nach diesen vorbereitenden Worten darf ich dazu übergehen, die Maschine zu erklären
und zu beschreiben.
I. Theoretische Grundlage des
Arithmometers.
Die einfache Operation des Zählens oder Addirens von Einheiten wird im Maschinenwesen bei den Zählwerken angewandt, mit welchen die Hübe von
Dampfmaschinen, die Umdrehungen von Wellen u.s.w. gezählt werden. Von einem solchen
Zählwerk, und zwar einem möglichst einfachen, will ich ausgehen, um dem Leser die
Rechenmaschine verständlich zu machen. Ich wähle hierzu ein Desbordes'sches Zählwerk von zwei Elementen (Fig. 1).
Textabbildung Bd. 165, S. 338
Von diesen letzteren besteht jedes in einem zehnzähnigen
Schaltrad, und zwar stehen die Zähne der benachbarten Schalträder immer
entgegengesetzt. Jedem Schaltzahn entspricht eines der zehn Zahlzeichen, die auf
einer mit dem Rad verbundenen Scheibe aufgetragen sind, und auf dem Zifferblatt des
Instrumentes durch runde
(hier punktirte) Oeffnungen einzeln sichtbar werden. In das Einerrad
A greift die Schaltklinke C,
D ein, welche bei Auf- und Abbewegung des Hebels E, F das Rad jedesmal um eine Zehnteldrehung weiter
schaltet, also nach jeder ganzen Schwingung des Hebels eine neue Ziffer am Schauloch
erscheinen läßt. Stand an diesem anfänglich die Null, so erscheint nach der neunten
Schwingung die 9, nach der zehnten aber wieder die Null. Für eine richtige Angabe
der Hubzahl sollte nun am Schauloch des Zahnrades
B eine 1 erscheinen, um anzugeben, daß 10 Einheiten
gezählt wurden. Dieß wird bewirkt durch den Zahn G,
welcher mit dem Einerrade fest verbunden ist. Derselbe kommt nämlich, wenn die 9
oben anlangt, in die hier punktirte Stellung, das Zehnerrad eben angreifend, und
schiebt dieses um eine Zehntel-Drehung weiter,
sobald A von 9 nach 0 fortschreitet. Stand B vorher auf 0, so erscheint nun eine 1, und es geben
nun die in den beiden Schaulöchern sichtbaren Ziffern in unserer gewöhnlichen
Schreibweise 10 an, daß 10 Schübe des Hebels erfolgt sind. Nach weiteren neun
Umdrehungen zeigt das Zifferblatt die Zahl 19, G ist
aber wieder in die punktirte Stellung gelangt, und bringt bei dem nächsten Schub bei
B die 2 zum Vorschein, während A auf 0 geht, und das Zifferblatt also die Zahl 20
zeigt. So wird man fortzählen können bis 99; der nächstfolgende Schub liefert 00. Es
ist aber klar, daß bei Hinzufügung eines dritten Elementes bis 100 und darüber bis
999 gezählt werden könnte, wenn nur immer die richtige Uebertragung der Zehner erfolgt. Denkt man sich noch Sicherheitsvorrichtungen hinzu, welche die Räder stets sicher in ihren
Stellungen erhalten, wenn gezählt ist, so sieht man ein, daß mit einem solchen
Zählwerk entsprechend unserer im Decimalsystem gebräuchlichen Form beliebig hoch
gezählt werden kann, wenn man nur die genügende Zahl von Elementen aneinander reiht.
Zu demselben Ergebniß führen andere gute Zählwerke; nebenbei gesagt, ist die Zehnerübertragung bei allen der wichtigste und meistens
schwierigste Punkt.
Mit der Herstellung eines solchen Decimalzählwerkes ist
aber schon ein bedeutender Schritt zur Rechenmaschine gemacht; denn wir brauchen
dasselbe nur zu erweitern, um schon eine Addirmaschine zu
erhalten. Ja zum Addiren könnte der Zähler schon so, wie er ist, dienen; denn man
brauchte, wenn zu einer gegebenen, in den Schaulöchern sichtbaren und einstellbaren
Zahl eine andere addirt werden sollte, ja bloß den Zählhebel so oft auf- und
niederzuschieben, als der neue Summand Einheiten hat. Doch wäre dieß natürlich von
einer unpraktischen Umständlichkeit. Um sie zu vermindern, wird man zunächst daran
denken müssen, für jedes Spiel das Schalten von nicht nur einem, sondern von mehr
Zähnen im Einerrad
möglich zu machen; eine Verdoppelung des Hebelhubes würde schon die Addition von je
2 Einheiten für jede Schwingung möglich machen, und unter Einschaltung passender
Mechanismen wird es auch unschwer erreichbar seyn, nach Belieben 1 oder 0 bis 9
Einheiten bei jedem Spiel zu addiren. Ein so vorgerichtetes Schaltgetriebe kann man
ein Decimalschaltgetriebe nennen. Mit seiner Hinzufügung
ist, wie man einsieht, vieles gewonnen. Fragt man sich aber, wie es zu machen sey,
daß bei einem Schub 10 Einheiten zugefügt werden, so kann dieß sofort auf zwei Arten
erreicht werden. Entweder gebe ich dem Einerrad für einen Hebelschub eine ganze
volle Umdrehung, so wird z.B. von 0 aus sofort bei A
wieder die 0, bei B aber vermöge der Zehnerübertragung
die 1, also zusammengelesen 10 erscheinen; oder ich kann ja auch die 0 in A stehen lassen, und schiebe nur B um ein Zehntel, d. i. um einen Zahn. Dann ist
mit einer einfacheren Bewegung des Mechanismus dasselbe erreicht, was vorhin durch
eine weit verwickeltere erzielt wurde. Träfe man nun auch am Zehnerrad die
Einrichtung von vorhin, bei welcher man es in der Hand hätte, nach Wunsch 0 bis 9
Einheiten in den Zehnern zu addiren, so könnte man damit
10, 20, 30, 40 u.s.w. Einheiten zur gegebenen Zahl auf einfache Weise addiren. Noch
mehr, lassen wir die beiden Schaltgetriebe (am Einer- und Zehnerrad) gleichzeitig (oder kurz nacheinander) wirken, so ist damit
die Möglichkeit gegeben, jede Zahl unter 100 bei einem
einzigen Hebelspiel zu einer in den Schaulöchern sichtbaren Zahl
hinzuzufügen. Z.B. um 13 zu 24 zu fügen, so würde man zunächst das Einerrad auf 4,
das Zehnerrad auf 2 stellen, sodann die beiden Schaltmechanismen so hinstellen, daß
bei einer Hebelschwingung am Einerrad 3 Zähne, am Zehnerrad 1 Zahn vorgeschoben
würde; alsdann würde das Vollziehen der Hebelbewegung im Einerschauloch 7, im
Zehnerschauloch 3, also zusammen die Summe 37 erscheinen lassen. Ja, und wir
brauchen nur der so erweiterten Maschine mehr Elemente von derselben Einrichtung zu
geben, um sofort eine rasch arbeitende Addirmaschine zu erhalten, praktische und
bequeme Handhabungsvorkehrungen selbstredend vorausgesetzt.
Einen Punkt aber müßten wir dabei noch etwas näher betrachten: die Zehnerübertragung. Gesetzt, auf unserer obigen kleinen Rechenmaschine,
bei welcher wir uns die obige Einstellbarkeit des Schaltwerkes hinzudenken wollen,
solle 11 zu 9 addirt werden. Dann ist das Einerrad auf 9, das Zehnerrad auf 0 zu
bringen, beide Schaltwerke aber so zu stellen, daß eine ganze Schwingung des
Schalthebels jedes der Räder um 1 Zahn vorschieben muß. Bedenkt man aber nun, daß
bei der Stellung 9 im Einerrade der Zehnerschalter G
gerade in Berührung
mit einem Zahn des Zehnerrades steht, so wird nun, wenn man die
Fortschiebungen wirken läßt, das Zehnerrad gleichzeitig
durch G und durch das Schaltwerk um 1 Zahn vorangedreht. Es kommt also von der Zehnerscheibe
die 1, von der Einerscheibe die 0 vor das Schauloch; das Resultat ist mithin 10
statt, wie es seyn sollte, 20. Es ist also geradeso, als ob
keine Zehnerübertragung stattgefunden hätte. Dieser Fehler, welcher auch
bei anderen Additionen leicht eintreten kann, muß vermieden werden. Das Mittel
hierzu ist nicht fernliegend. Man braucht nur das Schaltgetriebe des Zehnerrades
erst dann wirksam werden zu lassen, wenn die Zehnerübertragung
schon stattgefunden hat, oder stattgefunden haben könnte, oder umgekehrt:
die Zählung vor der Zehnerübertragung vor sich gehen zu
lassen. Dann wird in unserem obigen Beispiel zuerst am Einerrade die 0, und
gleichzeitig am Zehnerrade die 1 vortreten, darauf aber erst die Schaltung am
Zehnerrade anheben und dasselbe abermals um 1 Zahn weiter drehen, also die 2 vor das
Schauloch bringen, und das richtige Resultat 20 zum Vorschein kommen lassen.
Dieselbe nothwendige Eigenschaft des Schaltgetriebes auf die übrigen noch
hinzuzufügenden Elemente ausdehnend, erhalten wir das
Voreilen
resp. Nacheilen aller einzelnen
Schaltgetriebe vor den linksbenachbarten als nothwendige und zureichende
Bedingung für das richtige Wirken unserer bis jetzt construirten Additionsmaschine.
Nun aber ist dieselbe auch zu einer großen Vollkommenheit und Brauchbarkeit
gediehen. Leicht ist es nun, die nöthige Elementenzahl vorausgesetzt, folgende
Addition zu machen:
6437014036923471098–––––––1048838
Denn, stellen wir zunächst das Schaltwerk am Einerrade auf 1, am Zehnerrade auf 0, am
100-Rade auf 7, am 1000-Rade auf 3, am 10000er-Rade auf 4, am
100000er-Rade auf 6, so bringt eine ganze Schwingung des Schalthebels, im
Zifferblatte vorher lauter Nullen vorausgesetzt, sofort auf diesem den ersten
Summanden 643701 zum Vorschein; darauf stellen wir das Schaltwerk auf 403692,
bewegen den Hebel, und erhalten auf dem Zifferblatt die Summe 1047393, darauf im
Schaltwerk 347 eingestellt und den Hebel bewegt, zeigt sich die Summe 1047740, und
endlich, den Summanden 1098 im Schaltwerk einstellend und den Hebel bewegend, bringt
man die Hauptsumme 1048838 hervor.
Bemerkenswert ist, daß wir die Zwischensummen eigentlich nicht zu beachten, also mit
ihnen uns nicht aufzuhalten brauchen, sondern möglichst rasch auf die Hauptsumme zu
kommen suchen werden.
Wenn wir bisher nur stets ganze Zahlen vorausgesetzt
haben, so war das eine unnöthige Einschränkung. Unsere obigen Summanden hätten auch:
64,370140,36920,03470,1098
seyn dürfen, die Summe war dann richtig: 104,8838; wir mußten
bloß die einfache Vorsicht gebrauchen, im Schaltwerk die Stellung des Komma's zu
beachten, um eine fehlerfreie Addition zu machen, genau so,
wie wir es bei dem gewöhnlichen Verfahren auf dem Papier zu thun
pflegen.
Vielleicht wird mancher Leser an dieser Stelle den stillen Einwurf erheben, als sey
das erzielte Resultat nicht von der oben hervorgehobenen Bedeutung, indem das
Einstellen des Schaltwerkes kaum oder nicht so rasch gehen könne, als das
Zusammenzählen in der gewohnten Weise. Ueberhaupt zweifle ich nicht, daß mancher
geübte Rechner nur mit dem kopfschüttelnden Vorurtheil, als sey doch mit solchen
Mechanismen streng genommen nichts anderes auszurichten, als etwas niedliche
Spielerei, mir bisher gefolgt ist. Sein Vorurtheil hoffe ich später gänzlich zu
besiegen; doch will ich ihm in der That auf obiges Addiren theilweise und bis auf den Vorbehalt der Sicherheit in der
Maschinenoperation Recht geben; dennoch aber ist das, was wir oben erzielt haben,
etwas ganz Bedeutendes, weil damit unsere Maschine schon zur
Multiplication völlig fertig und geeignet ist.
Denn da „eine Größe mit einer anderen multipliciren“ nichts
anderes heißt, als sie so oft als Summand setzen als die zweite angibt, so braucht
man nur den einen Factor im Schaltwerk einzustellen, und darauf das Schaltgetriebe
so viele Spiele machen lassen als der andere Factor angibt, um darauf im
Zifferblatte das Product erscheinen zu sehen. Stellt man z.B. in unserem obigen
Rechenmechanismus das Schaltwerk auf 18 ein und läßt es 5 Spiele machen, so ergibt
sich oben aus 18 + 18 + 18 + 18 + 18 das Product 90. Ebenso wird, wenn das
Schaltwerk auf 3 gestellt ist, bei 27 Spielen das Product 27 × 3 = 81
hervorgehen, und man so überhaupt, eine genügende Elementenzahl in der Maschine
vorausgesetzt, mittelst ihr jede beliebige Zahl mit jeder
anderen vervielfachen können. Auch Decimalbrüche werden so multiplicirbar seyn, im
Resultat wird man dabei nur das Komma nach bekannten Regeln zu setzen haben.
Ist der Multiplicator groß, so muß man bei vorstehendem Verfahren das Schaltwerk sehr
oft spielen lassen. Im gewöhnlichen praktischen Rechnen benutzen wir aus ähnlichen
Gründen den einfachen Kunstgriff, mit den Zehnern, Hundertern etc. gerade so zu
multipliciren, wie mit den Einern, die jedesmaligen Producte nur ihrer Ordnung gemäß
zur Linken zu versetzen. Ganz entsprechend aber können wir
auch bei unserer Rechenmaschine verfahren. Wir multipliciren hierfür nur
zuerst den Multiplicanden, welcher im Schaltwerk eingestellt ist, mit den Einern des
Multiplicators, stellen darauf die Einer des
Multiplicanden (im Schaltwerk) beim Zehnerrad ein, die
Zehner beim Hunderterrad
ein, u.s.f. und multipliciren darauf mit der Zehnerstelle des Multiplicators u.s.w.,
und oben wird das richtige Product erscheinen. Wiederholen wir, um dieß Verfahren
anzuwenden, das obige Beispiel 27 × 3. 1) Im Schaltwerk steht der
Einerschalter auf 3: wir schalten 7mal und es zeigt sich oben die Zahl 21. 2) Wir
stellen den Einerschalter auf 0, den Zehnerschalter auf 3: schalten 2mal, und oben
erscheint in den Zehnern 3 × 2 mehr als dort schon stand (2), also 8 und im
Ganzen 81. Arithmetisch ist dieß auch sofort klar; denn wir haben mit der Verlegung
der 3 in die Zehner nichts anderes gethan, als die Zahl 30 eingestellt, welche Zahl
2mal hinaufaddirt, mit den vorhandenen 21 das ganze gesuchte Product 81
ausmacht.
Die Zahl der Schaltwerkspiele verminderte sich dabei bedeutend; statt 27 hatten wir
nur 7 + 2 = 9 Spiele zu machen; im Allgemeinen wird die Zahl
der Spiele nicht größer als die Quersumme des Multiplicators zu seyn
brauchen. Das Verlegen des Multiplicanden im Schaltwerk ist also äußerst
werthvoll. Ist die Zahl der Ziffern, welche verlegt werden sollen, groß, so wird das
fortwährend wechselnde Einstellen mühsam seyn; ungemein einfach dagegen würde es
sich auch dann bewirken lassen, wenn das ganze Schaltwerk von
rechts nach links und zurück von einer Zahlenscheibe zur anderen verlegt werden
könnte. Dieß läßt sich aber in der That unschwer einrichten, und dadurch
unser Apparat abermals wesentlich verbessern; ich will ein so vorgerichtetes
Schaltgetriebe ein verlegbares Schaltwerk nennen.
Immer noch beschäftigen wir uns mit dem obigen kleinen Decimalzählwerk, welches wir
in Gedanken nach und nach verbessert und bereichert haben; wir sind damit so weit
gelangt, eine schon sehr geschickte Additions- und Multiplicationsmaschine
gemacht zu haben. Ein Schritt noch, und wir haben die entgegenstehenden Operationen, das
Subtrahiren und Dividiren,
auch erreicht.
Unser Zählwerk wird nämlich sofort subtrahiren statt zu addiren, wenn wir auf allen
Zifferscheiben die 10 Zeichen umgekehrt ordnen, nämlich überall
statt:
0
1
2
3
4
5
6
7
8
9
die Folge:
9
8
7
6
5
4
3
2
1
0
anbringen. Dann werden, wie sofort einleuchtet, auf jeder
Zahlenscheibe stets so viele Einheiten rückwärts oder
abgezählt, als Zähne am Schaltrade vorgeschoben werden. Maschinell kann man jene
Vertauschung dadurch erreichen, daß man die Zifferscheibe von der Schaltscheibe
getrennt ausführt, und ihr deren Bewegung durch ein sogenanntes Wendegetriebe mittheilt, mittelst dessen man nach Willkür
die Scheiben rechts- oder linksläufig machen, sie mit den Schalträdern oder denselben entgegen zu
gehen zwingen kann. Ein solches Wendetriebwerk wollen wir an unserer obigen Maschine
noch eingefügt denken.
Haben wir dann mit derselben vorhin alle Eigenthümlichkeiten der Addition richtig zur
Erscheinung bringen können, so müssen sich jetzt auch alle diejenigen der
Subtraction mit ihr hervorbringen lassen, denn wir haben das Schaltgetriebe mit
seiner Zehnerübertragung ganz unverändert gelassen.
In der That, stellen wir die Scheiben im Zifferblatt nach geschehener Umkehrung des
Wendegetriebes z.B. auf 36, und den Einerschalter auf 1, den Zehnerschalter auf 0,
und lassen darauf das Schaltwerk 1mal spielen, so geht die Einerzahlenscheibe von 6
auf 5, beim nächsten Spiel von 5 auf 4, darauf auf 3, auf 2, auf 1 und beim sechsten
Spiel auf 0. Diese steht aber an der Stelle der 9 bei der Addition, welche letztere
bei Weiterschaltung um 1 Zahn den Zehnerübertrager wirken ließ. Dieß geschieht also auch jetzt. Der Zehnerübertrager
schiebt die Zehnerscheibe um 1 Zahn fort, es erscheint also statt der 3 bei uns die
2, während die Einerscheibe 9 zeigt, und es bleibt der richtige Rest, 29; mit
anderen Worten: die Zehner werden auch jetzt richtig übertragen.
Endlich ist die Division eine wiederholte Subtraction. Für dieselbe verfährt man auf unserer obigen
Rechenmaschine wieder ganz entsprechend der gewöhnlichen Uebung auf dem Papier. Daß
das Resultat richtig werden muß, liegt auf der Hand.
Wir haben also endlich aus dem einfachen Zählwerk, mit welchem wir begannen, durch
allmähliche Erweiterung eine Rechenmaschine gemacht, mit welcher man die 4 Species
rechnen kann. Nun aber ist die Thomas'sche Rechenmaschine in
der That nichts anderes,
als ein in dem bis hierhin besprochenen Sinne erweitertes
Zählwerk; sie ist nämlich, wie ich nunmehr definirend in kurzen Worten
zusammenfassen darf: ein Decimalzählwerk, welches mit einem
verlegbaren Decimalschaltgetriebe und einem Wendetriebwerk für die
Zifferscheiben versehen ist.
II. Form und Gebrauch des
Arithmometers.
Wenn sich oben die Thomas'sche Rechenmaschine in einem
kurzen Satze in Bezug auf ihre Zusammensetzung erklären ließ, und zwar so erklären,
daß ein geübter Cinematiker darnach den ganzen Zusammenhang der angewandten
Mechanismen überschauen kann, so ist dieß mehr der neueren Entwickelung der Cinematik oder Getriebelehre
zuzuschreiben, als der Einfachheit in der Anlage der Maschine. Freilich würden bei
Zugrundelegung einer ausgebildeten Getriebelehre ein Pascal und ein Leibnitz nicht jahrelang mit
geringem Erfolge nach der Maschine gesucht haben, und würde auch der heutige
Erfinder rascher damit vorgeschritten seyn. Dennoch blieb auch dann noch vieles
auszusinnen, zu versuchen, zu ergrübeln übrig, um das Ganze zu einem handlichen,
bequemen, „nicht difficilen“ Instrumente zu gestalten, wie es
der „Arithmometer“ in der That ist.
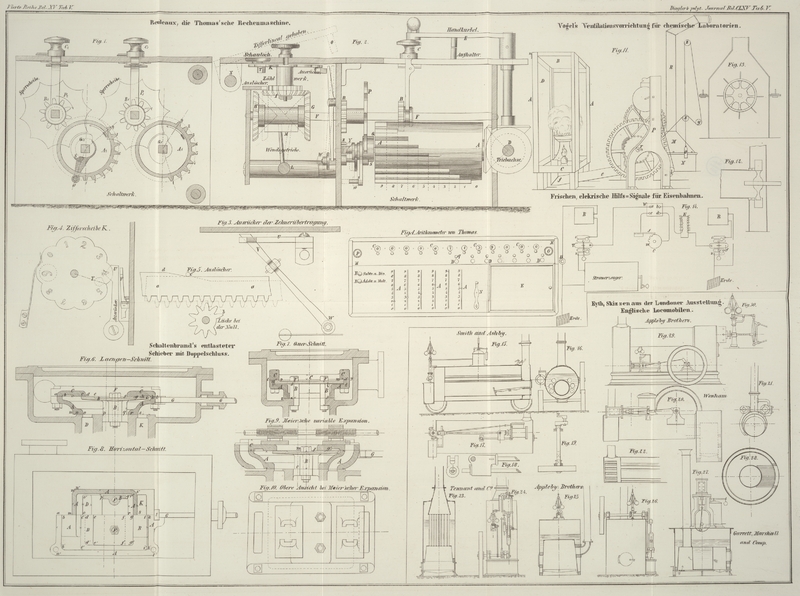
Die Figur A
auf Tab. V stellt einen solchen von mittlerer Elementenzahl dar, wie sie Thomas ausführen läßt. In einen 450 Millimet. langen, 160
Millimet. breiten und 70 Millimet. hohen Kasten ist der Mechanismus eingebettet, und
zwar liegen unter A, A die Schaltgetriebe, bei B, B die Handhaben des Wendetriebwerkes, bei C, C in
dem Lineal M, M die Zifferscheiben, und bei N die kleine Handkurbel zum Treiben des Schaltwerkes.
E ist eine kleine Schiefertafel und gleichzeitig
Deckel eines Behälters, in welchem sich u.a. einige elfenbeinerne Komma's zum Einstecken in die zwischen den Zifferscheiben
sichtbaren Löcher befinden.
Die Verlegbarkeit des Schaltwerkes unter den Zifferscheiben ist dadurch erreicht, daß
das Zifferlineal M, M über dem Schaltwerk verlegbar
gemacht ist. Hierfür hat es an der hinteren (oberen) Kante ein Gelenk, um welches
man es, den Knopf P anfassend, um jene Kante drehen und
vorn etwas aufheben kann; ist das geschehen, so läßt es sich links und rechts
schieben und von Schaltrad zu Schaltrad legen, so jedoch, daß man die letzte
Zifferscheibe links nicht weiter als bis vor das letzte offene Schaltgetriebe links
bringen kann, und ebenso die letzte Zifferscheibe rechts nur bis zum letzten
Schaltrad rechts. Diese Verlegungsgrenzen genügen. Leicht ist ferner einzusehen, daß
nicht so viel Schalter da zu seyn brauchen, als Zifferscheiben, da jeder Factor kleiner ist als das Product. Hier sind 12 Zifferscheiben und 6
verstellbare oder offene Schaltgetriebe vorhanden; zwei unverstellbare, welche für
weitgehende Zehnerübertragungen nöthig sind, liegen noch zur Linken unter der
Deckplatte.
Wird das Lineal vorne frei gehoben, so lassen sich mittelst der kleinen angedeuteten
Knöpfe die Zifferscheiben leicht verstellen, so daß man an jeder derselben jedes
beliebige der 10 Zeichen vor das Schauloch bringen kann. Auch lassen sich dann alle
gemeinschaftlich auf 0 stellen. Hierzu dient ein besonderer Auslösch-Mechanismus, den man durch Drehen des Knopfes 0 am rechten
Flügel des Lineals in Thätigkeit setzt. Die Einstellung der
einzelnen Schaltgetriebe erfolgt durch Verschiebung der bei A, A angegebenen Zeigerknöpfe. Die Ziffer, auf welche der Zeiger hinweist, gibt die Zahl der
Zehntel einer Drehung an, um welche das jedesmal über dem betreffenden Schlitz
liegende Zählrad gedreht wird, wenn das Schaltwerk ein ganzes Spiel macht, wenn
nämlich die Kurbel N eine ganze Umdrehung
durchläuft.
Die Kurbel
N kann bloß von links nach rechts aus ihrer jetzigen
Anfangsstellung gedreht werden, und muß für jedes Spiel wieder ganz bis in die
Anfangsstellung gebracht werden, zu deren leichter Auffindung ein Anschlagestift oder Aufhalter
angebracht ist.
Alle Operationen der Maschine bestehen nun aus folgenden einzelnen Operationen:
1) Einstellung der Zifferscheiben im Lineal M;
2) Einstellung der Schaltgetriebe bei den Schlitzen A;
3) Niederdrücken eines der beiden Knöpfe B, B, was die erfolgende Addition oder Subtraction vorbereitet;
4) Umdrehen der Kurbel N;
5) Verlegen des Lineals M.
Als Hauptwirkung der Maschine hat man sich nun einfach Folgendes zu merken: Jede
Zahl, welche man im Schaltwerk (bei A) einstellt, wird
durch eine Kurbeldrehung auf die Zifferscheiben hinaufgeschafft, und zwar positiv oder zugezählt zu der etwa dort vorhandenen Zahl,
wenn man den unteren der Knöpfe B niederdrückt, und negativ oder abgezählt, wenn man den oberen Knopf B niederdrückt. Hierin besteht das
ganze äußere Verhalten der Maschine, wobei nur zu bedenken ist, daß die
Zehnerübertragung stets von selbst richtig erfolgt. Die Knöpfe B können nur bei der Nullstellung der Kurbel N niedergedrückt werden (stets hebt sich der andere,
wenn man den einen niederpreßt), in allen übrigen Kurbelstellungen werden sie von
selbst in ihren Stellungen festgehalten. Beim Subtrahiren und Dividiren macht man
noch einen nützlichen Nebengebrauch von den Scheiben D, von denen
weiter unten mehr die Rede seyn wird.
Wir wollen nun die Maschine für die einzelnen mit ihr ausführbaren Rechenoperationen
in Gebrauch nehmen.
Addition. Alles auf 0 gestellt (das Lineal wird gehoben,
der Auslöscher O gedreht, und das Lineal wieder
eingelegt), der Additionsknopf niedergedrückt.
1. Beispiel. Man will addiren
716
zu
1325
––––––––––––––
Summa
2041.
Stelle in den 3 ersten Schlitzen (von rechts) die Zeigerknöpfe auf 716, und drehe die
Kurbel 1mal, so erscheint oben die Zahl 716; stelle darauf in den 4 ersten Schlitzen
die Zahl 1325 ein, drehe die Kurbel 1mal, so erscheint oben die Summe 2041.
2. Beispiel. Zu addiren 7,063 zu 131,0. Alles auf 0
gesetzt. Stelle im Schaltwerk ein:
Schalter
VI
V
IV
III
II
I
0
0
7
0
6
3
und bringe diese Zahl durch einmalige Kurbeldrehung hinauf;
stelle darauf den Schalter wie folgt:
Schalter
VI
V
IV
III
II
I
1
3
1
0
0
0
und drehe 1mal, so steht oben 138063; das Komma ist zwischen 8
und 0 zu setzen.
Subtraction. Alles auf 0 gesetzt; der Subtractionsknopf
wird gebraucht. Man bringt zuerst mit Addition den Minuend auf die Zifferscheiben,
stellt den Subtrahend in der richtigen Ordnung darunter im Schaltwerk ein, drückt
den Subtractionsknopf nieder und dreht 1mal, so erscheint oben der Rest.
1. Beispiel. Von 189 sey abzuziehen 75.
18975–––––114
Bringe in die Zifferscheiben 189, stelle mit den Einern unter Einer 75, drehe mit
Subtraction und es steht oben 114.
2. Beispiel. Zu bilden: 1759,6 – 684,57 –
15,043. Ausgelöscht. Stelle ein (mit Addition)
imSchaltwerk
VI
V
IV
III
II
I
die Zahl
1
7
5
9
6
0,
lege das Lineal so weit nach links, daß nur eine Stelle noch über das Schaltwerk hinausragt, dann
drehe um, lege das Lineal vollends nach links, worauf über dem Schaltwerk steht:
1
7
5
9
6
0
0
Im Schaltwerk
VI
V
IV
III
II
I
stelle dann ein:
6
8
4
5
7
0
drücke auf „Subtraction“ und drehe, so
erscheint oben:
1
0
7
5
0
3
0
über dem Schaltwerk;
VI
V
IV
III
II
I
stelle dann in diesem ein:
1
5
0
4
3
drehe, und es erscheint:
1
0
5
9
9
8
7.
Gesetzt man habe in der Eile die Kurbel 1/2 Umdrehung zu weit gedreht, so haben die
Zahlenscheiben angefangen, sich zu verstellen, das Resultat
ist fehlerhaft geworden. In solchem Falle vollende man ruhig die
überzählige Drehung (es erschiene dann bei uns 1 0 4 4 9 4 4), drücke auf
„Addition“ und vollziehe abermals
eine Drehung, so wird die fälschlich 1mal zu viel abgezogene
Zahl wieder addirt, und es kommt oben richtig:
1 0 5 9, 9 8 7
worin der Aufgabe entsprechend, das Komma nach der dritten
Stelle anzubringen ist. Zu bemerken ist, daß wir beim wirklichen Gebrauch der
Maschine das Zwischenresultat 1075030 nicht zu beachten, also z.B. nicht
aufzuschreiben brauchen.
Multiplication. Alles auf 0,
„Multiplication“ oder „Addition“
niedergedrückt.
1. Beispiel. Zu multipliciren 13 mit 6. Man stelle
(womöglich den unbequemeren Factor, hier z.B. die) 13 im Schaltwerk ein, und drehe
die Kurbel 6mal, so erscheint oben das Product 78.
2. Beispiel. Zu multipliciren 13495 mit 2514.
13495
2514––––––––– 53980 13495 6747526990–––––––––33926430.
Stelle das Schaltwerk auf 13495, und lege das Lineal, nachdem alle Zifferscheiben auf
0 gestellt oder ausgelöscht worden sind, ganz nach links. Darauf drehe für die Einer
des Multiplicators 4mal: oben erscheint 53980; verlege das Lineal um eine Stelle
nach rechts, und drehe für die Zehner (des Multiplicators) 1mal, oben erscheint 188930; verlege das
Lineal wieder um eine Stelle nach rechts und drehe für die Hunderter 5mal, so kommt
oben 693430; lege endlich das Lineal nochmals um eine Stelle nach rechts und drehe
für die Tausender 2mal, so kommt oben das richtige Product 33926430 zum Vorschein.
Die Zwischenresultate beachtet man beim Arbeiten mit der Maschine nicht, sondern
merkt bloß auf die Zahl der Drehungen und das Verlegen des Lineals.
3. Beispiel. Man kann auch mit den Stellen der höchsten
Ordnung (links) im Multiplicator anfangen, anstatt mit denjenigen der niedrigsten.
Zu multipliciren:
643917492398–––––––––––17063442966
Ausgelöscht. Den obersten Factor im Schaltwerk eingestellt, lege man das Lineal ganz nach rechts,
drehe
4mal,
verlege
das
Lineal
um eine
Stelle
nach
links,
„
9 „
„
„
„
„ „
„
„
„
„
2 „
„
„
„
„ „
„
„
„
„
3 „
„
„
„
„ „
„
„
„
„
9 „
„
„
„
„ „
„
„
„
„
8 „
so steht oben das Product, welches mit 35 Umdrehungen und 5
Verlegungen erzielt wurde, wozu 18 bis 21 Secunden erforderlich sind, das Einstellen
mit eingerechnet. – Beim Gebrauch von Logarithmen hätte man:
2 Logarithmen
mit Differenzen aufzuschlagen,
dieselben zu addiren,
die Summe aufzuschlagen,
und einige Differenzen nachzutragen gehabt,
ohne dabei die letzten Stellen des obigen Productes finden zu
können, was alles bei einem sehr geübten Logarithmenrechner kaum in weniger als 1
1/2 Minute hätte geschehen können. – Doch wollen wir obiges Beispiel noch
einfacher als oben rechnen.
4. Beispiel. Verkürzung der Multiplication. Wieder zu multipliciren:
643917492398–––––––––––10763442966
Ausgelöscht. Lineal ganz nach rechts. Den obersten Factor im Schaltwerk eingestellt.
Drücke „Multiplication.“ Sodann:
drehe 5mal (statt 4mal), verlege das Lineal um eine Stelle,
drücke „Subtraction,“
drehe 1mal, (50 – 1 = 49) verlege das Lineal um eine
Stelle, drücke „Multiplication,“
drehe 2mal, verlege das Lineal um eine Stelle,
drehe 4mal und verlege das Lineal um 2 Stellen,
drücke „Subtraction,“
drehe 2mal (400 – 2 = 398),
so ist das Product mit 14 Drehungen statt mit 35, wie oben,
erreicht worden; das Drücken der Knöpfe geht so leicht mit dem Daumen der Linken,
daß es keinen Mehraufwand an Zeit erfordert; die leicht verständliche Operation
fordert 15–17 Secunden Zeit.
5. Beispiel. Quadrirung. Beim Quadriren hat man den
Vortheil, den Multiplicator in dem eingestellten Multiplicanden vor sich zu haben.
Gesucht das Quadrat von 687,943.
Ausgelöscht; das Lineal bis auf eine Stelle nach rechts (weil 6mal 6 = 36 eine
weitere Stelle links liefert), die zu quadrirende Zahl im Schaltwerk eingestellt,
und verfahre wie vorhin, fo ergibt sich mit 6 + 8 + 7 + 9 + 4 + 3 = 37 Umdrehungen,
oder auch mit 7 + (– 1) + (– 2) + (– 1) + 4 + 3 = 18 Drehungen
das gesuchte Quadrat:
473265,571249,
von welchem 6 Decimalstellen abzuschneiden sind, da die Wurzel
deren 3 hat.
6. Beispiel. Zweifache Multiplication. Es sey das Product
349,04 . 57,63 . 0,073 zu bilden.
Auslöschen. Lineal nach links (wegen des bequemeren Abschneidens der Decimalstellen);
im Schaltwerk 349,04 eingestellt, mit 57,63 multiplicirt, gibt 20115,1752. Diese
Zahl wird auf die Schiefertafel E geschrieben, darauf im
Lineal alles ausgelöscht, und im Schaltwerk 73 eingestellt (wenn man vernachläßigen
durfte, wäre 20115,2 einzustellen gewesen), gibt 1468,4077896. Die 0 und die 2 zur
Linken waren hierbei durch Verlegung des Lineals nicht zu erreichen. Man versetzt
dann die Stellen 73 im Schaltwerk um eine Stelle nach links: keine Drehung, wegen
des Factors 0, Verstellung um eine weitere Stelle nach links: 2 Drehungen wegen des
Factors 2.
7. Beispiel. Verkürzte zweifache Multiplication.
Ausgelöscht. Lineal ganz nach links. Factor 349,04 im Schaltwerk eingestellt. Man
schreibt nun die beiden anderen Factoren auf die Schiefertafel E:
57,63 0,073
und bildet deren Product successive im
Kopf, was wie man sehen wird, gar nicht schwer ist, und dreht demgemäß die
Kurbel. Ausführung:
Man bilde
3 × 3 = 9,
drehe
9mal,
verlege
das
Lineal
um eine
Stelle,
3 × 6 = 18,
„
8 „
„
„
„
„ „
„
3 × 7 = 21, + 1 = 22,
„
2 „
„
„
„
„ „
„
3 × 5 = 15, + 2 = 17,
„
7 „
„
„
„
„ „
„
0 × 1 = 1,
„
1 „
und verlege das Lineal wieder nach links, jedoch wegen der
Stellung der 7 im Factor 0,073 nur mit der zweiten (Zehner-) Stelle über die
erste des Schaltwerkes, so daß dann steht:
6
0
3
4
5
5
2
5
6
über dem Schaltwerk
VI
V
IV
III
II
I
worin immer noch steht:
3
4
9
0
4
Man bilde nun weiter:
7 × 3 = 21,
drehe
1mal,
verlege
das
Lineal
um eine
Stelle,
7 × 6 = 42, + 2 = 44,
„
4 „
„
„
„
„ „
„
7 × 7 = 49, + 4 = 53,
„
3 „
„
„
„
„ „
„
7 × 5 = 35, + 5 = 40,
„
0 „
„
„
„
„ „
„
0 × 4 = 4,
„
4 „
und es erscheint das richtige Product:
1468,4077896
wovon wie oben 3 + 2 + 2 = 7 Stellen abzuschneiden sind. Die
Zahl der Drehungen betrug 39, das Schaltwerk brauchte nicht verstellt zu werden; es geschah die erzielte zweifache Multiplication in einer
Operation, während oben 2 Operationen mit 47
Umdrehungen und außerdem (zufällig) einer Schaltwerkverschiebung nöthig gewesen. Die
kleine Kopfrechnung geht, da sie nur von Stelle zu Stelle schreitet, sehr
leicht.
8. Beispiel. Cubicirung. Das Erheben einer Zahl in die
dritte Potenz geht sehr bequem bei Zugrundelegung der soeben besprochenen zweifachen
Multiplication. Zu cubiciren die Zahl 3421.
Auslöschen. Lineal nach links. 3421 im Schaltwerk eingestellt, und nun die
allmähliche Quadrirung von 3421 im Kopf vollzogen, und danach gedreht, liefert in 1
1/4 Minute den Cubus
40036787461.
Division. Auslöschen. Das Lineal ganz nach rechts, den
Dividenden ganz links hinaufgeschafft. Darauf drückt man die
„Division“ oder „Subtraction,“ stellt
den Divisor im Schaltwerk soweit als möglich links, und beginnt das Abziehen desselben von den letzten
Stellen zur Linken des Dividenden, bis der Rest zu klein geworden ist, die Zahl der
nöthigen Drehungen gibt dann die erste Stelle (von links) des Quotienten an. Darauf
wird das Lineal um eine Stelle verlegt und fortgefahren. Das Imkopfbehalten der
Umdrehungszahlen ist umbequem; um es zu ersparen, ist aber in unserer Maschine ein
besonderes Zählwerk D, das Quotientenzählwerk, kürzer der Quotient
genannt, angebracht. Bei demselben werden die Zeigerscheiben einzeln von der Hand
auf 0 gestellt, und nun erst beginnt man die Operation.
1. Beispiel. 2934 durch 3 zu theilen. Lineal nach links,
2934 hinaufgeschafft, so daß steht:
2
9
3
4
0
0
VI
V
IV
III
II
I
3
Darauf wird die 3 im Schaltwerk bei VI eingestellt: 3 von 2
geht nicht, wir stellen sie deßhalb unter die 9. Nun drehen wir, nachdem
„Division“ gedrückt ist. Nach 9 Drehungen sehen wir eine 2
oben bleiben, im Quotienten steht aber eine 9. Lineal um 1 Stelle nach links
verlegt, 7mal gedreht, bleibt 2, Lineal verlegt, 8mal gedreht, bleibt von 24 der
Rest 0. Im Quotientenzähler lesen wir 978 als Resultat der Rechnung. Will man die
Probe machen, so multiplicirt man nun den Divisor mit
der Zahl, welche im Quotientenzähler steht. Bei richtiger Operation muß dann oben
wieder der Dividend erscheinen, was auch bei uns der Fall ist.
2. Beispiel. 160 durch 13 zu theilen. Auslöschen. 160
hinaufschaffen; zur Verdeutlichung hinter die 0 einen Kommastift einstecken, 13
unter 16 im Schaltwerk einstellen. Quotientenzähler auf 0.
„Subtraction“ niedergedrückt.
Drehe 1mal, bleibt 3, erste Quotientenstelle = 1. Nun werde aus Versehen noch einmal
gedreht; dieß macht sich dadurch bemerklich, daß links eine 9 erscheint, im
Quotienten zeigte sich eine 2; durch das Erscheinen der 9 wird man stets sofort auf
den Fehler aufmerksam gemacht. Man drückt also „Addition“ und
dreht 1mal, addirt also die fälschlich abgezogene Zahl 13 wieder, und sieht oben
wieder 030...., im Quotienten die 1 erschienen. Lineal verlegt. 13 von 30 geht.
„Subtraction“ gedrückt und zweimal gedreht, läßt oben 4 als
Rest. Der Quotient ist also 12 4/13. Wir können aber weiter fortdividiren, und den
gemeinen Bruch in einen Decimalbruch verwandeln. Lineal
verlegt:
Drehe
3mal,
bleibt 1,
verlege
das
Lineal
um 1
Stelle,
„
0 „
„ 10,
„
„
„
„ 1
„
„
7 „
„
9,
„
„
„
„ 1
„
Drehe
6mal,
bleibt 12,
verlege das Lineal um 1 Stelle,
„
9 „
„
3,
das Lineal ist ganz nach links verlegt,
und wir haben als Quotienten: 12,30769. Zur Probe damit
rückwärts multiplicirend, kommt wieder 160 nach oben, vom Komma ab gelesen. Hätte
man noch mehr Stellen haben wollen, so brauchte man nur den Rest 3 wieder nach links
auf die letzte Zifferscheibe zu bringen, um beliebig weit fortfahren zu können.
Unendliche Decimalbrüche können so mit großer Leichtigkeit bis zu jeder nur
irgendwie wünschbaren Stellenzahl gerechnet werden.
3. Beispiel. 1 durch 75 zu theilen. Auslöschen. 1 ans
linke Ende des Lineals stellen, dieses ganz nach rechts. Quotient auf 0 gestellt. 75
in 1 geht nicht, in 10 ebenfalls nicht, Lineal nach links verlegt, 75 in 100 geht
1mal, bleibt 25, Lineal verlegt, nach 3 Drehungen bleibt 25, Lineal verlegt, 3
Drehungen liefern stets den Rest 25, und so ins Unendliche. Quotient also:
0,013333....
Wurzelausziehung. Die Ausziehung der Quadratwurzeln geht
auf dem Arithmometer verhältnißmäßig einfach, doch nicht viel schneller, als die
logarithmische Rechnung. Wegen des Verfahrens verweise ich auf die von Thomas dem Instrument beigegebene Anweisung.
Bei uns sind vortreffliche Wurzeltafeln auch so verbreitet, daß man sich in den
meisten Fällen der technischen Praxis mit denselben helfen kann. Ueberhaupt muß hier
hervorgehoben werden, daß man wohl beachten muß, daß die Rechenmaschine nicht für
alle und jede Rechenoperation gleichschnell arbeitet und arbeiten kann, so daß, wer
schnell rechnen will, sich der Rechenmaschine da bedient, wo sie besser und
schneller zum Ziele führt, aber zu anderen Mitteln greift, wo ihm solche bessere
Dienste leisten können. Diejenigen, welche mit der Maschine zu arbeiten haben,
werden sich bald eine Combination von Rechnungsmitteln bilden, die sie den Umständen
stets anpassen, dann aber damit auch außerordentlich rasch arbeiten.
Zum Schluß dieser Anleitung will ich noch einige Beispiele nicht so abstracter Natur,
wie die bisherigen waren, vorführen, woran man erst so recht eigentlich die
Vorzüglichkeit des Instrumentes wird ermessen können.
1) Gesetzt es sey eine Tafel für die Gewichte der Gußeisenplatten zu rechnen, deren
Dicken von Millimeter zu Millimeter steigend angenommen werden sollen, und bei denen
man das Gewicht in Kilogrammen pro Quadratmeter wissen
will. Bei 1 Millimeter Plattendicke ist der Inhalt des zu betrachtenden Körpers
gerade 1 Kubikdecimeter, dessen Gewicht in Kil. also gleich dem specifischen
Gewicht, welches bei dem betreffenden Gußeisen durch genaue Methoden = 7,244 gefunden sey. Dieß
vorausgesetzt, stellen wir die Zahl 7,244 im Schaltwerk ein, drücken auf
„Addition“ und haben:
nach
1
Umdrehung
für 1
Millimeter
Plattendicke
d. Gewicht
7,244k
„
2
„
„ 2
„
„
„ „
14,488k
„
3
„
„ 3
„
„
„ „
21,732k
„
4
„
„ 4
„
„
„ „
28,976k
„
5
„
„ 5
„
„
„ „
36,220k
u.s.f.; jede Umdrehung liefert einen
Werth der aufzustellenden Tabelle.
2) Man habe eine Formel y = c√x, z.B. die Dicke d eines schmiedeeisernen Zapfens für die Last P in Kil.
d (in Millimetern) = 9/8√P
und will für die Werthe d = 20,
25, 30, 35, 40, 45, 50 etc. die Belastungen P in einer
Tabelle zusammenstellen, so ermittelt man sich zunächst:
P = (8/9)² d² = 0,790123 d²,
legt dann die Quadratentafel vor sich (z.B. Weisbach's Ingenieur S. 16), stellt 709123 als Factor in
dem Schaltwerk ein, richtet sich auf „Multiplication“ und
braucht nun als Factoren die in der Tafel sich findenden Quadrate der
Unveränderlichen d. Also
bei d =
20 den Factor
400 und
erhält
rasch
P =
316,049
25
„ „
625 „
„
„
414,815
30
„ „
900 „
„
„
711,111
35
„ „
1225 „
„
„
967,901
40
„ „
1600 „
„
„
1264,197
u.s.w. und bedenke nur, daß bei logarithmischer Rechnung
jedesmal 1 Log. verdoppelt, dazu ein anderer gezählt werden, darauf ein Numerus zu
der Logarithmensumme gesucht werden müßte.
3) In Zeuner's mech. Wärmetheorie findet sich u.a. in
Tabelle I eine Spalte mit den berechneten Werthen
Q = 606,5 + 0,305 t,
wobei die Temperaturen t von 5 zu
5 Graden steigen. Diese Formel erfordert auf dem gewöhnlichen Wege nach vorheriger
Aufschlagung des log. zu 0,305:
Aufschlagung des log. zu t,
dessen Addition zu log. 0,305,
Aufsuchung des Numerus zur Summe,
Addition derselben zu 606,5.
Es seyen 3 Decimalstellen gewünscht.
Wir bereiten uns folgendermaßen vor. 606,500 hinaufgeschafft, das Komma eingesteckt,
305 im Schaltwerk so eingestellt:
606,500
305
Darauf drehen wir 5mal, und erhalten oben 608,025 als Werth
für t = 5. Darauf verlegen wir das
Lineal um 1 Stelle nach rechts, was bei jeder Drehung 10 × 0,305
hinaufaddirt, und erhalten nun bei jeder Drehung einen
Tabellenwerth, nämlich:
nach
1
Drehung
für
t = 15
den
Werth
611,075
„
2
„
„
t = 25
„
„
614,125
„
3
„
„
t = 35
„
„
617,175
„
4
„
„
t = 45
„
„
620,225
u.s.f.; die Zahlen werden schneller erhalten, als sie
aufschreibbar sind! Um die Zwischenstufen zu erhalten, fängt man wieder bei t = 0 an, addirt 10 ×, 20 ×, 30 ×
0,305 u.s.f.
4) In derselben vorgedachten Tabelle findet sich eine Spalte nach der Formel
r = 607 – 0,708 t
berechnet, ebenfalls für die obigen Stufen von t. Wir verfahren ganz ähnlich. 607,000 wird
hinaufgestellt; darunter im Schaltwerk 0,708 so:
607,000
708
Darauf drückt man den Subtractionsknopf, dreht 5mal, und es erscheint oben der Werth für t = 5, nämlich 603,460. Nun das Lineal um 1 Stelle nach
rechts gelegt, erhält man für jede Drehung wieder einen
Tabellenwerth.
5) Formeln von der Form y = (x² + 27,43 . x)/(x – 2), der Schrecken der Logarithmenrechner, lassen sich spielend
auf dem Arithmometer ausrechnen. Sey z.B. x = 22,54, so
verfahren wir folgendermaßen:
Alles ausgelöscht. Lineal ganz nach links.
Im Schaltwerk folgendermaßen eingestellt:
Lineal:
0
0
0
0
0
0
0
0
0
0
0
0
VI
V
IV
III
II
I
2
2
5
4
Bilde nun das Quadrat von 22,54. Es erscheint, wenn man das Lineal zurückgelegt
hat:
0
0
5
0
8,
0
5
1
6
0
0
VI
V
VI
III
II
I
2
2
5
4
in welcher Zahl man das Komma richtig zwischen 8 und 0
einsetze. Darauf multiplicire man, unter Belassung des niedergedrückten
Additionsknopfes, 22,54 mit 27,43; es erscheint oben sofort der ganze ausgerechnete
Zähler 1126,3238. Im Schaltwerk zieht man nun in der fünften Spalte den Zeigerknopf
von 2 auf 0, und verlegt das Lineal wie folgt:
0
1
1
2
6
3
2
3
8
0
0
VI
V
VI
III
II
I
2
0
5
4
stellt den Quotienten auf 0, drückt auf
„Subtraction“ und dividirt; alsbald kommt als Endresultat: 54,835 und zwar beansprucht die ganze
Rechnung den vierten Theil der Zeit, die man braucht, um vorstehende Erklärung zu
lesen.
Diese Beispiele sollten, wie ich glaube, genügen, um das Instrument in seinem
Gebrauch und seiner großen Brauchbarkeit kennen zu lehren, so daß ich nun zur
näheren Beschreibung des Mechanismus übergehen kann.
III. Beschreibung der Construction des
Arithmometers.
Nach den Erklärungen, welche unter (I) gegeben wurden, und nachdem wir uns soeben mit
den Aeußerlichkeiten des Arithmometers bekannt und vertraut gemacht haben, dürfen
wir es unternehmen, in das scheinbar so verwickelte innere Getriebe des Instrumentes
untersuchend hineinzuschauen. Auf Tab. V sind die wichtigsten Details desselben für
zwei Elemente (Einer und Zehner) dargestellt, und zwar in der 1,7fachen Größe der
Ausführung, wobei ich mir indessen der Deutlichkeit zu Liebe einzelne kleine (für
die Ausführung unpraktische) Aenderungen erlaubt habe. Das Ganze zerfällt auch hier
wieder in Schaltwerk, Zählwerk und Wendegetriebe. Zwischen Schaltung und Zählrad sitzt sodann wieder die
wichtige Zehnerübertragung.
Der Haupttheil jedes Schaltgetriebes ist die Schaltwalze
A, A₁, A₂,
Fig. 1 und
2.
Dieselbe ist zusammengesetzt zu denken aus zehn niedrigen Cylindern, von denen der
erste keinen, der zweite 1, der dritte 2, der vierte 3 u.s.w., der zehnte 9 Zähne
hat, welche hier 1/22 Umfangs zur Theilung haben. Diese Zähne können mit dem Rädchen
B, B₁, B₂
in Eingriff gebracht werden, indem man dasselbe mittelst des Zeigerknopfes C, C₁, C₂ auf
seiner vierkantigen Achse verschieben, und beliebig über die 9, 8, 7, 6-
u.s.w. zähnige Stelle der Schaltwalze bringen kann. Der Erfolg ist, da B 10 Zähne hat, daß dasselbe um 9, 8, 7, 6 u.s.w.
Zehntel-Umdrehungen verstellt wird, wenn A eine
Umdrehung macht. Sämmtliche Schaltwalzen des Instrumentes werden aber vermittelst
der Haupttriebachse D, welche die ganze Maschine entlang
läuft, stets
gleichzeitig einmal umgedreht, wenn man die Handkurbel E
eine Drehung machen läßt. Der Griff der letzteren ist, wie hier gezeichnet,
niederlegbar.
Die Achse F des Rädchens B
treibt mit einem der kleinen Kegelräder G oder H des Wendegetriebes das Rad I auf der senkrechten Achse, welche die Zifferscheibe K trägt, und ertheilt demnach der letzteren in positivem
oder negativem Sinne eben so viele Zehnteldrehungen als B empfängt. Die Achse L des Umstellers des
Wendegetriebes geht unter den sämmtlichen Achsen F her,
ebenso wie die flache Stange M, welche die Büchse
zwischen den Rädchen G und H
erfaßt und deren Hin- und Herschiebung unmittelbar bewirkt. Das Zifferlineal
dreht sich um die Achse N. Man sieht ein, daß in der
gehobenen (hier punktirten) Stellung desselben sämmtliche Zifferscheiben außer
Eingriff mit dem Getriebe kommen müssen. Das sichere Wiedereinkehren der Zahnräder
wird durch eine Reihe Einschnitte vermittelt, in welche der Stift O einsinkt, sobald man das Lineal an den richtigen
Stellen niederläßt.
Alle Zifferscheiben sind, wie es in Fig. 4 angegeben ist,
außen mit 10 Bogenbauchungen versehen, welche eben so viele Sperrzähne vorstellen,
in welche eine weiche Feder eingreift, um die Scheiben mit einiger Kraft in den
Stellungen zu erhalten, wo die Ziffern sich gerade dem Schauloch gegenüber befinden.
Diese Sperrung ist aber noch nicht genügend, um fehlerhafte Einstellungen der
Zifferscheiben, insbesondere der die Bewegung vermittelnden Rädchen zu verhüten.
Vielmehr sind hierfür noch besondere Sperrräder P,
P₁, P₂ in den Schaltgetrieben
angebracht.
Ein solches Sperrrad besitzt 10 gleiche bogenförmige Ausschnitte, in welche das
Sperrstück Q, Q₁, Q₂ auf der Schaltwalzenachse eingreift. Dieses Sperrstück Q hat aber, wie die punktirten Linien deutlich machen,
eine gerade so weit reichende Einziehung, daß nicht gesperrt wird, so lange es möglich ist, daß Schaltzähne in das Rädchen B eingreifen. Mithin bewirkt die beschriebene
Einrichtung, daß die Drehung des Rädchens und der zugehörigen Zifferscheibe
freigegeben ist, sobald der verzahnte Bogen zu B tritt,
sobald also die Achse des Zahnes 9 sich der Eingriffstelle nähert und während des
ganzen Zahnbogens 9–1 freigegeben bleibt, nach Durchgang desselben aber
wieder getrennt wird. Hierdurch wird einem Verkehrtstellen der Zifferscheiben durch
Erschütterungen bei raschem Drehen u.s.w. vorgebeugt. Zugleich freilich erschwert
diese notwendige Einrichtung die Construction der Zehnerübertragung, die deßhalb
mehr Theile erhalten mußte, als man zu erwarten geneigt seyn möchte.
Die Zehnerübertragung wird zunächst bewirkt durch den an einem besonderen Arme sitzenden Zahn
10, welcher auf A, als der Einerwalze, nicht nöthig ist, auf jeder folgenden Walze aber angebracht
seyn muß. Der Zehnerzahn dürfte in das Rädchen B
eingreifen; da aber dieses hin- und hergeschoben werden muß, ist seine genaue
Wiederholung in dem unverschieblich auf F angebrachten
Rädchen R vorhanden. In dieses kann der Zahn 10 nur dann
eingreifen, wenn er sich in der (in Fig. 2) punktirten Lage
befindet. Soll er aber eingreifen, so muß dann gleichzeitig das Sperrwerk P, Q gelöst werden. Dieß geschieht nun wie folgt.
Das Sperrstück Q besitzt in einer weiter rechts von P belegenen Ebene noch eine weiter zurücktretende Stufe
S, welche das Sperrrad im Falle des Eingriffes des
Zehnerrades ungehindert läßt, wenn sie in seine Ebene gebracht wird. Solches
geschieht aber gleichzeitig mit dem Vorschieben des Zehnerzahnes in die Ebene von
R, indem jener Zahn mit dem Sperrstück aus einem
Ganzen besteht (mit ihm eintrumig ist). Das Uebertragen eines Zehners muß geschehen,
wenn beim Addiren die Einerscheibe von 9 auf 0, beim Subtrahiren, wenn sie von 0 auf
9 geht. Bei diesem Uebergang stößt aber der Zahn T der
Zifferscheibe (Fig.
4) einmal links, einmal rechts an den Vorsprung des Ausrückers U, dieser drückt dann auf den Zwischenhebel V, welcher das auf seinem Stift festgeschraubte
Tellerchen W und damit das Köpfchen X verschiebt, welch letzteres das Sperrstück und sein
Zubehör nach vorne zieht. Sobald dieß geschehen ist, was an irgend einem Punkte des
Eingriffes der ersten Schaltwalze vorkommen kann (z.B. gleich bei Eingriff des
ersten Zahnes, wenn im Zifferrad eine 9 stand und addirt wird), ist die Zehnerübertragung vorbereitet. Sie erfolgt aber
erst wirklich, wenn der Zehnerzahn nach oben und in Eingriff kommt, was aber erst
geschieht, wenn alle übrigen 9 Zähne schon durch die Eingriffstelle gegangen sind,
also möglicherweise gewirkt haben. Dann erst fällt der Zehnerzahn ein, schaltet um
1/10 Drehung, und läßt sofort wieder die Kante bei S in
das Sperrrad eingreifen, um jede Störung unmöglich zu machen.
Nun aber muß auch der Zehnerzahn wieder beseitigt werden, damit er bei der nächsten
Drehung nicht unnöthiger- oder fälschlicherweise nochmals schaltet. Zu dem
Ende ist an dem Sperrstück Q eine Schraubenfläche Y angebracht, welche gegen einen festen Stift Z stößt, an diesen streift und Q wieder an seine alte Stelle schiebt. Z ist
gerade so gestellt, daß sofort nach geschehener
Zehnerschaltung Q wieder zurückgebracht wird. Damit aber
gehen auch X, W, V und U
wieder zurück, und alles ist zu neuen Operationen in Bereitschaft gesetzt. Eine auf
W drückende und daran reibende platte Feder hält
dieses Tellerchen und die anhängenden Theile in ihren eingenommenen Stellungen fest. Diese sämmtlichen, so
sinnreich angebrachten Theile arbeiten mit einer erstaunlichen Sicherheit und
Schnelligkeit, und lassen in der That ohne ganz sonderbare Zufälle nie einen Fehler
aufkommen.
Schon oben wurde hervorgehoben, daß die einzelnen Schaltgetriebe stets einander vor- oder nacheilen
müssen, damit die Zehnerübertragung richtig erfolgen kann. Hier ist das Nacheilen gewählt; es beträgt von Walze zu Walze eine Zahntheilung, wie auch an unseren Walzen A₁, A₂ zu
bemerken ist. So kommt es, daß der letzte, der Einerzahn
in jedem Getriebe durch den Eingriffspunkt schon gegangen ist, wenn der des links
folgenden (also einer höheren Ordnung angehörigen) zur Wirkung kommt. Ist nun in
irgend einem Rade die Zehnerübertragung vorbereitet, so wird sie dieses Nacheilens
wegen stets auch ausgeführt. Nothwendig muß aber deßhalb auch, um Fehler zu
vermeiden, der leere Bogen auf der Schaltwalze angebracht
seyn. Die Größe derselben richtet sich nach der Zahl der angewandten Elemente. Die
hier benutzte Größe reicht für 8 zählende (einstellbare) Schaltwalzen noch
vollkommen aus. – Interessant ist es, die Wirkung der Zehnerübertragung beim
Addiren von Zahlen zu beobachten, welche aus vielen Neunen bestehen. Stellt man im
Zählwerk 0999999, im Schaltwerk aber nur eine einzige 1 in den Einern ein und dreht
nun einmal, so geschieht Folgendes. Der Zahn 1 in A₁ schaltet B₁ um einen Zahn herum;
dadurch wird aber für A₂ die Zehnerübertragung
vorbereitet, und nach Durchlaufung der folgenden Theilung auch vollzogen; hierdurch
bereitet sich für A₃ die Zehnerübertragung vor,
um sofort vollzogen zu werden u.s.f. Kurz man sieht bei langsamem Vollziehen der
Kurbeldrehung von links nach rechts eine 0 um die andere in den Schaulöchern die 9
ersetzen, und endlich links von der sechsten Stelle eine 1 statt der 0 vortreten, so
daß das richtige Resultat 1000000 da steht. Aehnlich aber umgekehrt wirkt die
Maschine, wenn man 1 von 1000000 abzieht, wo sofort 6 Neunen nacheinander zum
Vorschein kommen.
Das Hebelwerk des Wendegetriebes wurde weggelassen, da dasselbe ja leicht auf
vielerlei Arten gleichgut eingerichtet werden kann. Damit es fest steht, so lange
die Kurbel sich nicht in ihrer (hier gezeichneten) Anfangslage befindet, legt sich
einer der Hebel an eine Scheibe an, welche auf der letzten Schaltgetriebwelle zur
Linken sitzt. Diese Scheibe, welche bei jeder Kurbeldrehung eine Umdrehung macht, hat einen radialen Ausschnitt, welcher sich dem obigen Hebel gerade gegenüberstellt, wenn die
Kurbel auf 0 steht, dann also dem Hebel gestattet, auf die andere Seite der Scheibe
zu treten, wenn man den betreffenden Knopf drückt.
Außer dieser Einzelheit wurden auch noch manche andere weggelassen, z.B. das
Zählwerk des Quotienten. Von demselben ist zu bemerken, daß es stets nur
von der Einerachse A₁ des Schaltgetriebes aus in
Bewegung gesetzt wird, und zwar stets nur eine Scheibe desselben ohne Zehnerübertragung, weil beim Dividiren niemals
größere Einzelquotienten als 9 vorkommen. – Bemerkenswerth ist noch der Auslöscher, welcher in Fig. 2 zu bemerken, in
Fig. 5
theilweise detaillirt ist. Die Auslöschung wird durch eine Zahnstange bewirkt,
welche für gewöhnlich nicht in die zugehörigen Drehlinge b auf den Zifferscheibenachsen eingreift. Verschiebt man aber die
Zahnstange, was durch Drehen an einem Knopf bewirkt wird, der einen stets in sie
eingreifenden besonderen Drehling umtreibt, so zwingt die Schiefebene cd, am Stift c
hingleitend, die Zahnstange zum Eingriff mit den Rädchen b, und nöthigt diese sämmtlich, sich zu drehen. Diese Rädchen,
ursprünglich 10zähnig, haben aber der 0 gegenüber keinen Zahn, und werden demnach,
sobald die 0 im Schauloch erschienen ist, nicht ferner von der Zahnstange ergriffen.
Es müssen also alle Zifferscheiben sehr rasch auf 0 kommen, sobald man die
Zahnstange, deren Triebdrehling durch eine Spiralfeder stets wieder zurückgetrieben
wird, einigemal hin- und hergehen läßt.
Was im Allgemeinen die Handhabung der Maschine angeht, so ist nur weniges darüber zu
sagen. Gute Einölung ist wichtig, übrigens auch einfach. Am besten ist, den ganzen
Mechanismus, welcher sich sehr leicht aus dem Kasten nehmen läßt, bis an die
Deckplatte in ganz feines Oel einzutauchen, ihn einen Tag lang abtropfen zu lassen,
um dann in Gebrauch zu nehmen. Man braucht dann in dieser Beziehung nie mehr
nachzusehen. Schutz vor Staub ist selbstverständlich nothwendig, wofür übrigens der
sehr schön gearbeitete Kasten alles Nöthige leistet. Ein leichtes und schnelles Drehen an der Kurbel
wird bald zur Gewohnheit, so daß man bald schon durch das Gefühl belehrt wird, ob
eine etwaige kleine Stockung durch einen zwischen die Rädchen gefallenen fremden
Gegenstand, oder etwa unzeitgemäßes Aufheben oder Senken des Lineales hervorgerufen
wurde. Ein leises Rütteln an der Kurbel beseitigt fast immer sofort die Störung;
über das Nachsehen bei besonderen Fällen findet sich das Nöthige in der Thomas'schen Anweisung.
Sollte ich ein Urtheil über die Zusammensetzung der Maschine und die Zweckmäßigkeit
in der Wahl der Theile aussprechen, so könnte dieses zunächst nur ein anerkennendes
seyn, da die gestellte Aufgabe vollkommen und mit compendiösen und leicht zu
fertigenden Theilen gelöst ist. Dennoch bleibt meines ernstlichen Erachtens die
Möglichkeit, noch größere Vereinfachungen anzubringen, die sich übrigens mit der
Zeit schon einführen werden. Die Hauptsache bleibt, daß man etwas gutes, praktisches
und nicht zu theures schon vor sich hat, also ungesäumt
zuerst anerkennen und benutzen soll.
Schlußbemerkungen.
Wenn es mir gelungen seyn sollte, die Aufmerksamkeit der Leser auf die wichtigen
Punkte hingeleitet und ihnen die Maschine nach Zweck, Wirkung und Einrichtung klar
gemacht zu haben, so muß auch der Zweifelsüchtigste darunter die Vortheilhaftigkeit,
den Werth, die Bedeutung der Erfindung bereits zugegeben haben. Vortheilhaft für
alles praktische Rechnungswesen, werthvoll für die Wissenschaft, bedeutungsvoll als
Erzeugniß menschlicher Denkkraft ist das Rädergetriebe in dem zierlichen
Ebenholzkasten, das sich erkühnt, Gedankenoperationen
auszuführen, wie ein Spiel. Noch ist der Arithmometer im deutschen Vaterlande wenig
verbreitet, aber ich bilde mir ein, in kurzer Zeit einen kleinen Dank bei vielen
erworben zu haben, die sich zu seiner Anschaffung entschließen werden. Vor allem
aber werden Dank und Anerkennung, höchste Anerkennung dem Erfinder gezollt werden
müssen. Sehen wir, wie es damit bestellt ist.
Thomas hat etwa 30 Jahre lang Mühe, Zeit- und
Geldaufwand angelegt, um seinem Instrument die heutige Vollkommenheit zu verleihen;
und, lernen wir die Einzelheiten seines Vorgehens kennen, so müssen wir den Muth,
die Zielklarheit und die Genialität hoch bewundern, mit welcher er nach und nach
alle Schwierigkeiten überwand. Diesem gegenüber sind der öffentlichen Anerkennungen
in Frankreich eigentlich nicht viele gewesen. 1822 sprach die
Aufmunterungsgesellschaft in Paris dem Erfinder ihre Anerkennung aus: 1851 verlieh
dieselbe Gesellschaft ihm eine goldene Denkmünze; in demselben Jahre stellte ihm die
Londoner Ausstellungsjury eine (einfache) Preismedaille zu; 1854 sprach sich die
Akademie in Paris sehr günstig über den Arithmometer aus und ließ ihn zur Preisbewerbung zu. Das ist ungefähr alles.
Der Monthionpreis wurde aber einer anderen, jetzt bei
Seite gesetzten Rechenmaschine, dem „Arithmaurel“, wie ihn die HHrn. Maurel und Sayet nannten, zu Theil, ein
Mechanismus, welcher nach Vorgang des Thomas'schen dessen Mechanismen zum Theil benutzt hatte.
Diese stillen Anklagen werden lebhaft in Frankreich erhoben, namentlich durch Régnier in seiner Histoire des nombres (Paris 1855), und man kann wohl nicht umhin,
dieselben gerecht zu finden.
Das Ausland hat mehr gethan als Frankreich. Freilich will ich dem Leser nicht
vorgreifen in dem ironischen Gefühl, welches ihm überkommen wird, wenn er den Bey von Tunis 1851 den Reigen eröffnen sieht, um mit einem seiner
höchsten diamantblitzenden Orden den Erfinder zu schmücken. Ihm folgen 1852 Franz I. von Neapel, dann der König der Niederlande, und
ein deutscher Fürst, der Herzog
von Nassau; dann 1853 der Papst, 1853 ebenfalls der Großherzog von Toscana,
1854 der König von Sardinien. – Und Deutschland? und die deutschen gelehrten
Gesellschaften und Ingenieurvereine?
Man darf erwarten, daß sie alle mehr oder weniger ihre Anerkennung für eine Erfindung
von so unbestreitbarem Werth ausgesprochen haben würden, wenn sie den Gegenstand
genügend gekannt und beachtet hätten. Deßhalb ist auch in dieser Beziehung das
Bekanntmachen des Arithmometers von Wichtigkeit, und ich glaube darum nicht bloß
meinen Fach- und bisherigen Leidensgenossen im Zahlenrechnen dadurch einen
Dienst zu erweisen, sondern auch einen Pflichtschuldigen Versuch des Dankes gegen
den Erfinder durch Veröffentlichung seiner Maschine zu machen.
Der Preis des Arithmometers ist hoch, wenn man seinen
Verbreitungskreis betrachtet, niedrig, wenn man die Schwierigkeiten in seiner
Herstellung ins Auge faßt. Hr. Thomas, glücklicherweise
in einer Lage, welche ihm keineswegs pecuniären Gewinn an seiner Erfindung zur
Nothwendigkeit macht, ermöglicht durch Zuschüsse eine verhältnißmäßig billige
Anfertigung der Maschine, welche mit wachsender Verbreitung indessen auch rasch
billiger werden wird.
Das große Instrument von 8 und 16 Stellen mit Quotient kostet
jetzt
400 Fr.
dasselbe ohne Quotient
300 „
das 6 und 12stellige, welches für die allermeisten Fälle
genügt, mit Quotient
300 „
das 5 und 10stellige
150 „
Sich zu wenden an Hrn. A. M. Hoart, rue du Heller, 13, in Paris. Für solche, die es wünschen sollten, erbiete
ich mich gerne, die Anschaffung und Wahl der Größe des Instrumentes zu
vermitteln.
Tafeln