| Titel: | Notiz über rotirende Räderverbindungen; vom Ingenieur C. Wasserzieher. |
| Autor: | C. Wasserzieher |
| Fundstelle: | Band 171, Jahrgang 1864, Nr. XXIII., S. 114 |
| Download: | XML |
XXIII.
Notiz über rotirende Räderverbindungen; vom
Ingenieur C.
Wasserzieher.
Mit Abbildungen auf Tab.
II.
Wasserzieher, über rotirende Räderverbindungen.
In Sanborn's Seil-Spinnmaschine, Bd. CLXVI S. 328
dieses Journals, kommen Räderverbindungen vor, welche ungewöhnlich und deßhalb nicht
sofort zu übersehen sind.
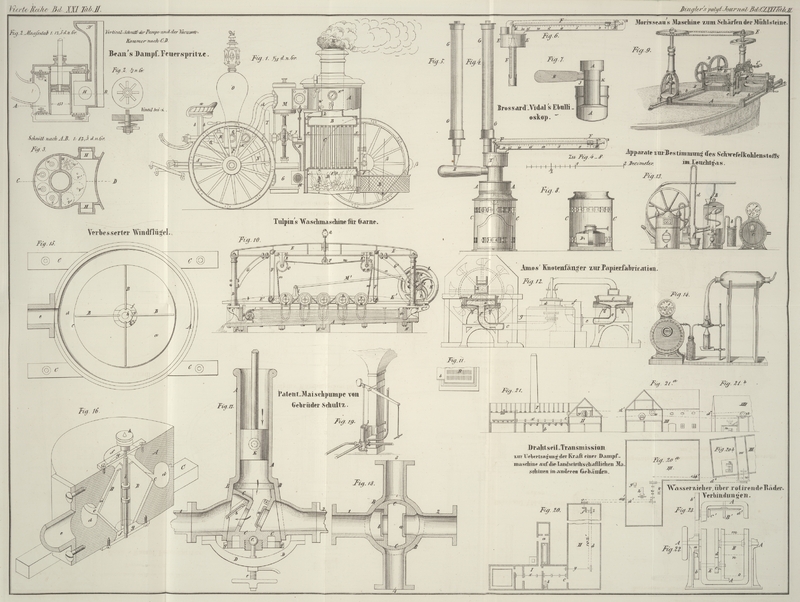
a, Fig. 22, ist ein
feststehendes Rad, A ein Rahmen mit zwei Zapfen, welcher
concentrisch zu a rotirt; mit ihm die Wellen E und B. B macht außerdem
eine Drehung, erzeugt durch die Räder a, d, c, d.
Ist z die Zahl der Umdrehungen des Rahmens A; sind a, b, c, d die
Zahnzahlen oder die Durchmesser der entsprechenden Räder, so macht B
x = z (1
– (a . c)/(b . d))
Umdrehungen. Wird x positiv, so
finden die Drehungen von B im gleichen Sinne statt, wie
die von A; wenn negativ, so im entgegengesetzten.
Daraus sieht man, daß durch diese Anordnung x im
entgegengesetzten Sinne von z beliebig groß gemacht
werden kann; im gleichen Sinne stets kleiner als z bleibt. Kann man indeß a und b oder d und c in Riemscheiben
umwandeln, oder eines der vier Räder mit innerer Verzahnung herstellen, so kann x auch im gleichen Sinne von z beliebig groß werden. Die Achse von B kann
natürlich in einer Linie mit der von A liegen, wie in
Fig. 22
dargestellt, oder beliebig excentrisch gegen letztere wie bei m, n oder o, oder auch gegen die Ebene der
Zeichnung beliebig vor- oder zurücktretend.
Sobald aber B' nicht mehr parallel A, sondern etwa wie in Fig. 23 angeordnet ist,
wird einfach
x = z
(a. c')/(b'. d').
Diese Betrachtung nützt vielleicht bei der Construction solcher Verbindungen.
Langenberg, bei Stettin, im December 1863.
Tafeln