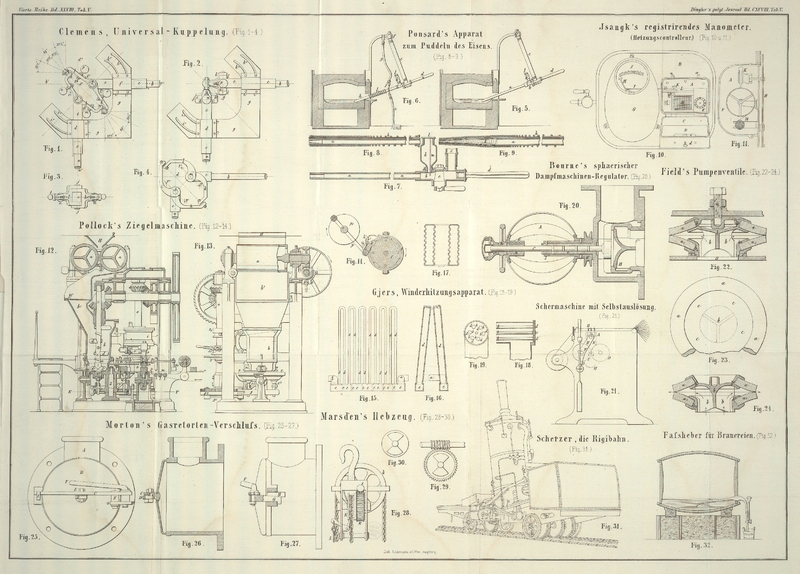
| Titel: | Universalkuppelung von Melville Clemens in Boston (Amerika). |
| Fundstelle: | Band 198, Jahrgang 1870, Nr. LXIII., S. 265 |
| Download: | XML |
LXIII.
Universalkuppelung von Melville Clemens in Boston
(Amerika).
Mit Abbildungen auf Tab.
V.
Clemens, Universalkuppelung.
Das Problem, zwei unter variablem Winkel in einer Ebene liegende Wellen derart zu
kuppeln, daß die getriebene Welle demselben
Bewegungsgesetze folge wie die treibende, hat neuerdings durch den Amerikaner
Melville Clemens in Boston eine recht einfache Lösung
gefunden.
Nachstehend folgt nach Engineering, September 1870, S. 179 eine Beschreibung dieser
Universalkuppelung, welche in Fig. 1 bis 4 abgebildet ist; außerdem
schließt Ref. eine kurze theoretische Betrachtung über die Richtigkeit der Lösung
der gestellten Aufgabe an.
Die beiden zu kuppelnden Wellen a und b, welche sich in Figur 1 im Punkte d' unter einem Winkel von 90 Grad schneiden, tragen an
den einander zugewendeten Enden die Hülsen c und e, mit welchen sie sich in den Lagern d und f drehen. Diese Lager
sind auf einer Platte g befestigt, von welcher am Schluß
des Artikels noch einmal die Rede ist.
i und h sind zwei gleichlange
Gelenkarme, welche durch den Bolzen j mit der Hülse c verbunden sind; auf ähnliche Weise werden die
gleichlangen Arme l und k
durch den Bolzen q mit der Hülse e in Verbindung gebracht.
Der Arm i der Welle a ist mit
dem Arm l der Welle d durch
das Kugelgelenk t, ebenso wie die Arme h und k durch das Gelenk s verbunden.
Es können demnach die bezeichneten Arme h, i, k und l ihrer Länge und Lage nach durch die Linien js und jt sowie
durch qs und qt
dargestellt werden.
Bei der Rotation der Wellen a und b bleiben die Schnittpunkte ihrer Achsen a'
d'' und c'
b' mit den Mittellinien ihrer zugehörigen Zapfen j und q fix, während die
Mittelpunkte der Kugelgelenke s und t sich in einem gemeinschaftlichen Kreise bewegen,
welcher in Fig.
1 senkrecht auf der Linie jq steht, dieselbe halbirt und als
Gerade st projicirt erscheint.
Die für die Arme h und i in
Betracht zu ziehenden Linien js und jt beschreiben bei der Rotation die Fläche eines
geraden Kreiskegels mit dem Scheitel inj.
Aehnliches gilt von dem Arm k und l, richtiger gesagt von den Linien qs
und qt, indem diese einen congruenten Kegel,
jedoch mit dem Scheitel in q beschreiben.
Beide Kegel haben eine gemeinschaftliche Grundfläche, welche von den Wellenachsen im
Punkte d' geschnitten wird und den Winkel (a'd'c') der letzteren halbirt.
Die Gelenkarme h, i, k und l
bewegen sich um die Achsen ihrer zugehörigen Wellen mit der gleichen
Winkelgeschwindigkeit wie diese selbst.
Es dreht sich demnach die durch die Wellenachse a'd'' und durch die Linien js und jt bestimmte Ebene, welche der
Kürze halber mit A bezeichnet sey, mit derselben
Geschwindigkeit, nach dem gleichen Gesetz wie die Welle a. Ganz dasselbe gilt von der durch die Mittellinie b'c' der Welle b und
die Linien qs und qt gelegten Ebene – kurz mit B
bezeichnet – deren Winkelgeschwindigkeit übereinstimmt mit jener der Welle
b.
Nach dem Vorausgegangenen genügt es daher, die Rotation der Ebenen A und B zu betrachten, um
von dieser auf die Drehbewegung der Wellen a und b zurück zu schließen.
Es wird nun zur Durchführung des Beweises, daß die getriebene Welle genau demselben
Bewegungsgesetze folge wie die treibende, hinreichen, zwei Stellungen α und α' der
Ebene A anzunehmen und zu zeigen, daß der dabei
zurückgelegte Winkel ebenso groß ist als jener, welcher durch die zwei
correspondirenden Stellungen β und β' der Ebene B
eingeschlossen wird.
In der Bildebene der Figur 1 fallen die Ebenen A und B zusammen; deren Anfangsstellung α resp. β ist somit gegeben.
Als zweite, beliebig gewählte Stellung α' der
Ebene A gelte jene, für welche der Punkt t nach t* (Figur 1) gelangt. Dieser
Punkt t* gehört als Mittelpunkt des Kugelgelenkes t auch der Ebene B in der
Stellung β' an.
Ohne Rücksicht auf den Winkel, welchen beide Wellen a und
b unter sich einschließen (in der Abbildung ist
derselbe, wie erinnerlich, mit 90 Grad angenommen), kann der Beweis, daß beide
Ebenen α und β' mit den Ebenen α und β, gleichbedeutend mit der Bildebene in Fig. 1, den gleichen Winkel einschließen, nachfolgend geliefert
werden.
Textabbildung Bd. 198, S. 267
Es bezeichnet im vorstehenden Holzschnitt b'd'd'' die
Bildebene resp. die Anfangsstellung α und β der beiden Ebenen A
und B.
t'' ist die orthogonale Projection des Punktes t* in der Bildebene.
Die Winkel t* t₁, t'' und t* t₂ t'' stellen die
Neigungswinkel der Ebenen αα' resp. ββ' dar und deren Gleichheit läßt
sich aus der Congruenz folgender Dreiecke nachweisen.
Es ist
d' t'' = d'
t''
< d' t₁ t'' = < d' t₂
t'' = 90°
und als Halbirungswinkel sind
Textabbildung Bd. 198, S. 267
Hieraus ergibt sich aber
t₁ t'' = t₂ t''
Ferner ist
< t₁ t'' t*, = < t₂
t'' t* = 90°
und
t'' t* = t''
t*
somit
Textabbildung Bd. 198, S. 267
und deßhalb
< t* t₁ t'' = < t* t₂
t''
oder mit Worten: Die Winkel der Ebenen αα' und ββ' sind einander gleich, d.h. die Drehung der einen Welle
bewirkt die Drehung der anderen um denselben, gleich großen Winkel.
Während die Wellen a und b
gleichförmig rotiren, drehen sich die vier Gelenkarme mit ungleichförmiger
Geschwindigkeit um die Verbindungslinie der Zapfenmittelpunkte j und q. Innerhalb einer
ganzen Umdrehung traten zwei Maxima und zwei Minima der Geschwindigkeit eines jeden Armes ein. Diese
Ungleichförmigkeit in der Drehung der Gelenkarme zieht Erschütterungen und deßhalb
eine erhöhte Abnutzung der Zapfen und Gelenke nach sich, deren Größe von der Form
und den Massen der Arme abhängt.
Um diesen Uebelstand so viel als möglich zu verringern, schlägt Clemens verschiedene Mittel vor.
Nach dem einen soll jeder Arm für sich ausbalancirt werden, indem man denselben so
weit nach rückwärts, über die Welle hinaus verlängert, daß sein Schwerpunkt in die
Mittellinie seines Zapfens fällt.
Eine andere Abhülfe gegen die schädlichen Erschütterungen bestände darin, daß je
zwei, zu derselben Welle gehörige Arme gegenseitig ausbalancirt werden. Dieß
erreicht man durch Anbringung von durch Schrauben stellbaren Gewichten m, n, o und p (Figur 1) an den
Armen h, i, k und l, wodurch
die Schwerpunkte der letzteren nach q', r', s' und t' verrückt
würden. Dabei ist die Lage dieser Schwerpunkte so auszumitteln, daß die
Verbindungslinie q'
r' durch das Zapfenmittel j,
ebenso wie s't' durch q geht.
Figur 4 zeigt
eine Gelenkconstruction, bei welcher die Schwerpunkte der Arme durch deren
eigenthümliche Form in eine ähnliche Lage wie in Figur 1 durch die
Anbringung der Gewichte gebracht wurden.Die angeführten Mittel zur Ausgleichung der Stöße scheinen aus dem Grunde
ungenügend, weil die Mittelpunkte der Massen mit den Schwerpunkten nicht
zusammenfallen. Die Erfahrung muß daher zeigen, ob es nicht zweckmäßiger ist
– mit Hinweglassung aller die Arme wohl ausbalancirenden, aber die
ungleichförmig schwingenden Massen nur vermehrenden Gewichte –, die
Erschütterungen durch möglichst leichte Anordnung der Arme so viel als
thunlich unschädlich zu machen. J.
Z.
Bei der Construction der beschriebenen Universalkuppelung hat Clemens die Winkel welche die Gelenkarme in der durch Figur 1 dargestellten Lage
mit den zugehörigen Wellenachsen einschließen, gleich 22 1/2 Grad gemacht, wohl nur
aus dem Grunde, um den Armen bei ihrer Bewegung nach allen Richtungen gleichviel
Spielraum zu lassen und um eine möglichst große Aenderung des von den Wellen a und b eingeschlossenen
Winkels zu gestatten.
Eine solche Aenderung ist deßhalb zulässig, weil die gemeinschaftliche Lagerplatte
g mit Schlitzen i'' und
k'' versehen ist, um den Lagern d und f als Führung zu
dienen. Die Schlitze sind kreisförmig und liegt der Mittelpunkt in j, beziehungsweise in q.
J. Z.
Tafeln