| Titel: | Rädermechanismus für Aufwickelung von Garn auf conische Spulen, von John Boyd in Glasgow. |
| Fundstelle: | Band 199, Jahrgang 1871, Nr. XCII., S. 353 |
| Download: | XML |
XCII.
Rädermechanismus für Aufwickelung von Garn auf
conische Spulen, von John
Boyd in Glasgow.
Nach Engineering, Januar 1871, S. 20; aus der
deutschen Industriezeitung Nr. 7.
Mit Abbildungen auf Tab.
X.
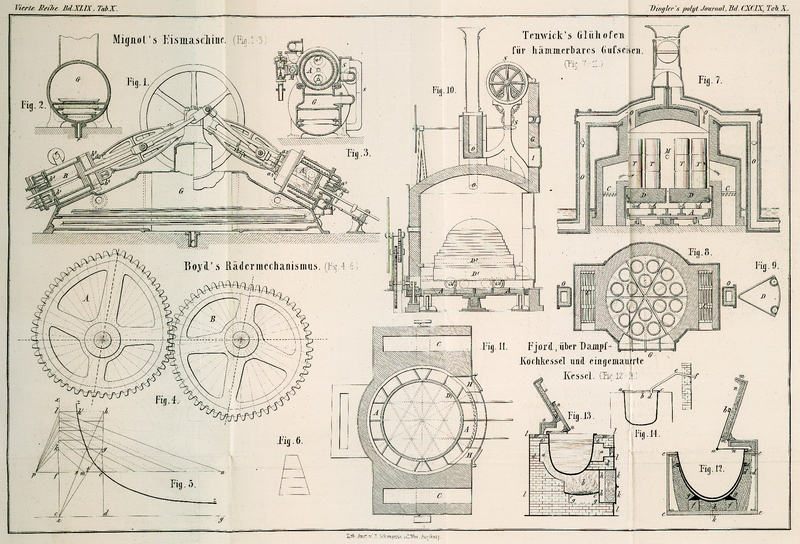
Boyd's Rädermechanismus für Aufwickelung von Garn auf conische
Spulen.
Der Rädermechanismus welchen sich John Boyd kürzlich in
England patentiren ließ, soll ermöglichen Garn mit gleichmäßiger Geschwindigkeit auf
conische Spulen aufzuwickeln. Die Räder machen eine halbe Umdrehung, während das
Garn sich nach aufwärts auf der Spule aufwickelt und ebenso während die Aufwickelung
nach unten zu erfolgt; jedes Rad besteht daher aus zwei symmetrischen Hälften. In
Fig. 4
bezeichnet a ein derartiges treibendes und b ein getriebenes Rad. Die Construction der Räder beruht
darauf, daß im treibenden Rad bestimmte Radien bis zum Theilkreis gezogen werden,
welche gleich einer Reihe äquidistanter Ordinaten sind, die in einer Hyperbel nach
deren Asymptote gezogen werden; werden dann die Längen dieser Ordinaten einzeln von
der Mittelpunktsentfernung beider Räder abgezogen, so erhält man die Radien, welche
im getriebenen Rad nach entsprechenden Punkten des Theilkreises gezogen werden. Die
abgebildeten Räder sind für conische Spulen bestimmt, bei denen der Halbmesser der
größten Grundfläche sich zu dem der kleinsten wie 2 1/2 : 1 verhält. Die punktirt angegebenen Halbmesser
theilen den halben Umfang eines jeden Rades in 16 Sectoren, von denen die im
treibenden Rad ungleiche, die im getriebenen gleiche Winkel haben. Durch
nachstehende Formeln lassen sich die einzelnen Radien des getriebenen Rades für jede
beliebige Eintheilungszahl des halben Umfanges und für jedes beliebige Verhältniß
der größten und kleinsten Spulen-Halbmesser berechnen. Es ist nämlich die
Länge x eines Halbmessers im getriebenen Rad, der um n Sectoren von dem kürzesten Halbmesser absteht, während
der halbe Umfang in N Sectoren getheilt ist:
Textabbildung Bd. 199, S. 354
wobei noch a den
Mittelpunktsabstand beider Räder und r die Zahl
bezeichnet, welche angibt wievielmal der größte Spulenhalbmesser größer ist als der
kleinste. Der kürzeste und längste Halbmesser lassen sich durch die Formeln 2a/(r + 3) und 2ar/(3r + 1) berechnen.
Geometrisch oder durch Zeichnung lassen sich die Halbmesser am geeignetsten in
folgender Weise finden (Fig. 5). Mit der Seite cd, welche den Abstand a zwischen den Rädermittelpunkten in geeigneter Verjüngung darstellt,
construire man das Quadrat cdef. Nachdem man den
längsten und kürzesten Halbmesser für das getriebene Rad berechnet hat, trägt man
dieselben von e aus als es und et auf der Seite ef auf und zieht durch die so bestimmten Punkte
gerade Linien von c nach der verlängerten Linie ed, z.B. nach g und
h. Die Länge eg
läßt sich auch durch die Formel 2a/(r + 1) und eh durch
die Formel 2ar/(r + 1)
berechnen.
Man theilt nun gh in N
Theile (in Fig.
5 sind der Einfachheit wegen nur 4 angenommen) und zieht durch gh und die einzelnen Theilpunkte Senkrechte hl, gk etc. zur
Verlängerung fl der Seite cf, sowie von c aus
gerade Linien nach allen Theilpunkten von gh.
Endlich trage man auf den zu fl senkrecht
gezogenen Geraden von gh aus Abstände hh' etc. auf, welche gleich sind den Abständen es etc., in welchen die von c aus gezogenen Geraden die Linie ef
schneiden. Die so bestimmten Punkte h' etc. liegen in
einer Hyperbel und die von gh aus aufgetragenen
Längen hh' sind die Längen der gleich weit von
einander abstehenden Halbmesser im getriebenen Rad. Die Stücke h'l etc, also die Ordinaten zwischen der Hyperbel
und ihrer x Asymptote cl'
geben die Halbmesser des treibenden Rades an den Punkten des Theilkreises, welche
mit den bereits
gefundenen Theilkreispunkten des getriebenen Rades zusammenfallen müssen. Diese
Punkte, welche im getriebenen Rad um gleiche Winkel von einander abstehen, sind im
treibenden um ungleiche Winkel von einander entfernt. Der erste dieser ungleichen
Winkel berechnet sich nach der Formel
Textabbildung Bd. 199, S. 355
Die anderen Winkel erhält man dadurch, daß man zur Differenz
zwischen den zunächst vorhergehenden noch eine nach der Formel
Textabbildung Bd. 199, S. 355
berechnete Größe hinzu addirt. So sind z.B. die Winkel für das
in Fig. 4
dargestellte treibende Rad für N = 16, r = 2 1/2
folgende
1.
6°
43'
48''
9.
82°
15'
56''
7°
19'
57''
12°
9'
14''
2.
14°
3'
45''
10.
94°
25'
11''
7°
56'
7''
12°
45'
24''
3.
21°
59'
52''
11.
107°
10'
35''
8°
32'
17''
13°
21'
34''
4.
30°
32'
8''
12.
120°
32'
9''
9°
8'
26''
13°
57'
43''
5.
39°
40'
35''
13.
134°
29'
52''
9°
44'
36''
14°
33'
53''
6.
49°
25'
11''
14.
149°
3'
45''
10°
20'
46''
15°
10'
3''
7.
59°
45'
56''
15.
164°
13'
48''
10°
56'
55''
15°
46'
12''
8.
70°
42'
51''
16.
180°
0'
0''
11°
33'
5''
der Unterschied in den Differenzen ist 36' 9,6.''
Eine gerade Linie mn (Fig. 5) läßt sich in
folgender Weise so theilen, wie der halbe Umfang des treibenden Rades. fp und fm werden
gleich eg gemacht, von p werden nach k und l und den übrigen Theilpunkten von kl
gerade Linien und von k, l und den übrigen auf kl befindlichen Theilpunkten Senkrechte km, in
etc. auf pk, pl etc. gezogen; die Durchschnittspunkte dieser
Senkrechten mit der Linie mn theilen letztere in
gewünschter Weise. Die Radien für das treibende Rad erhält man, indem man die Länge
mn in gleiche Theile theilt und von den
Theilpunkten, wie in Fig. 5 durch punktirte Linien angedeutet, nach bekannten Methoden gerade
Linien nach kl der Art zieht, daß dieselben auf
den Verbindungslinien, die von p nach ihren
Durchschnittspunkten mit kl gezogen werden,
senkrecht stehen. Werden dann durch diese auf kl
gelegenen Durchschnittspunkte Senkrechte auf xx
gezogen, so sind die Theile derselben, welche zwischen der Hyperbel und den Asymptoten xx liegen, die gesuchten Längen. Die Linie kl wird dann in demselben Verhältnisse getheilt,
wie ein Halbkreis durch die ungleichen Winkel, welche in dem getriebenen Rade den
gleichen Winkeln des treibenden Rades entsprechen. Die ungleichen Winkel des
getriebenen Rades können auch in der Weise erhalten werden, daß man ein
Paralleltrapez, welches einem Achsendurchschnitt des conischen Spulentheiles gleich
oder ähnlich ist (Fig. 6) durch Parallelen zur Basis in so viel gleiche Flächentheile
theilt, als das halbe Rad Sectoren hat. Die Theilungslinien schneiden dann die
Seiten des Trapez so, daß sich die einzelnen Längentheile zur ganzen Seite verhalten
wie die einzelnen gesuchten Linien zu 180°.
Die Spulen brauchen nicht gerade genau die gleichen Verhältnisse zu haben wie die,
für welche die Räder construirt sind; ist aber ein Unterschied vorhanden, so soll
die Differenz zwischen dem größten und kleinsten Spulendurchmesser eher kleiner als
größer seyn, wie die, für welche die Räder berechnet sind.
Die gewöhnliche Herzscheibe des Fadenführers, welche den Faden über die einzelnen
Theile der Spulenoberfläche führt, sitzt auf dem getriebenen Rade. Der Faden wird
annähernd in Form einer continuirlichen conischen Spirale aufgewickelt und die im
Obigen angegebenen Formeln etc. basiren auf der Annahme daß die Länge einer solchen
Spirale gleich der Summe der Umfänge der mittleren Kreise der einzelnen Windungen
ist. Diese Voraussetzung weicht von der mathematischen Genauigkeit nur um einen für
die Praxis ganz unmerklichen Betrag ab und um so weniger, je größer die Zahl der
Windungen zwischen den beiden Endflächen der conischen Spule ist.
Tafeln