| Titel: | Luftpyrometer mit Luftcompressionsmanometer; von Giovanni Codazza. |
| Fundstelle: | Band 210, Jahrgang 1873, Nr. XLII., S. 255 |
| Download: | XML |
XLII.
Luftpyrometer mit Luftcompressionsmanometer; von
Giovanni
Codazza.
Auszug aus den Atti della Reale Academie delle Scienze di
Torino vol. VIII. Sitzung vom 2. März 1873.
Mit Abbildungen auf Tab.
IV.
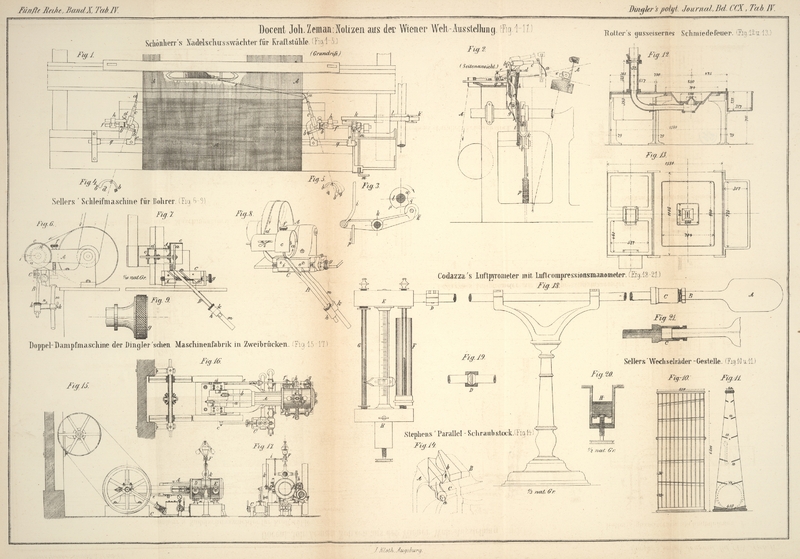
Codazza's Luftpyrometer mit Luftcompressionsmanometer.
Die Messung hoher Temperaturen bietet große Schwierigkeiten dar. Eine der besseren
seitherigen Methoden gründet sich auf das Eintauchen eines bis zur Temperatur des zu
untersuchenden Raumes erhitzten Versuchskörpers, in Wasser, aus dessen
Temperaturerhöhung man die Temperatur des ersteren berechnet. Behufs der Anwendung
dieser Methode ließ ich einen Apparat construiren, bei welchem jeder Anlaß zu einem
Irrthum hinwegfiel, und der genaue Indicationen darbot. Aber die Art, mit diesem
Apparate zu experimentiren, erfordert große Vorsicht.
Da mir die mit der Messung einer sehr hohen Temperatur verbundenen Schwierigkeiten
nicht entgingen und ich erkannte, wie schlecht in dieser Hinsicht die auf die
Dissociation der Körper sich gründenden Pyrometer mit freien Luftmanometern sich
bewähren, so sah ich mich genöthigt, zu einem Manometer mit comprimirter Luft meine
Zuflucht zu nehmen. Bei dieser Gelegenheit drängte sich mir unwillkürlich der
Gedanke auf, als pyrometrischen Körper ein Gas und zwar Luft anzuwenden, welche
durch die ganze Temperaturscala, innerhalb deren man experimentirt, eines und
dasselbe Gesetz der Ausdehnung beibehält. Für Pyrometer dagegen, welche sich auf die
Dissociation gründen,Man s. die Mittheilung ihres Erfinders (Lamy) im
polytechn. Journal, 1870, Bd. CXCV S. 525. ist es nöthig, mit der Aenderung der Temperaturgrenze einen anderen
pyrometrischen Körper zu nehmen, und um die Beziehung zwischen der Spannung der
dissociirten Gase und der Temperatur aufzustellen, bedarf es einer Messung der
letzteren mittelst eines sehr exacten Pyrometers. Das Luftthermometer in Verbindung
mit dem freien Luftmanometer ist bekannt.
Dem Elasticitätsgesetz der Gase läßt sich folgende Fassung geben: Die Producte aus dem Volumen und dem Drucke einer und
derselben Gasmasse in zwei verschiedenen Zuständen verhalten sich, wie ihre
absoluten Temperaturen in diesen Zuständen.
Indem man daher entweder den Druck oder das Volumen auf ein constantes Maaß reducirt,
erhält man eine einfache Relation als Maaß der Temperatur. Regnault construirte sein Thermometer, indem er bei jedem Versuche das
Volumen auf ein constantes Maaß reducirte und den Druck beobachtete, welchen ein
freies Luftmanometer anzeigte.
Auch das von mir vorgeschlagene Pyrometer ist ein solches von constantem Volumen.
Wenn aber die Temperatur eine gewisse Grenze überschreitet, und mit ihr der Druck
noch um einige Atmosphären steigt, so ist ein freies Luftmanometer nicht mehr
praktisch anwendbar; daher die Nothwendigkeit, dem Apparat ein Manometer mit
comprimirter Luft beizugeben. Dieses ist der einzige principielle Unterschied
zwischen meinem Pyrometer und Regnault's Luftthermometer.
Gegen das meinem Apparate zu Grunde liegende Princip läßt sich nichts einwenden; um
aber mit dem Apparate genaue Indicationen zu erzielen und ihn zugleich praktisch
bequem einzurichten, hatte ich noch verschiedene Schwierigkeiten zu überwinden.
Fig. 18
stellt mein Pyrometer in der Seitenansicht dar; die Figuren 19, 20 und 21
repräsentiren einige Details desselben. Seine Haupttheile sind: das zwiebel-
oder flaschenförmige Porzellangefäß A, welches den
thermometrischen Körper enthält; das Manometer mit comprimirter Luft, welches so
construirt ist, daß die in dem Apparat enthaltene Luft immer auf ein constantes
Volumen reducirt werden kann; endlich das eiserne Rohr, welches das Gefäß A mit dem Manometer verbindet. Der Umstand, daß dieses
Rohr zum Theil selbst in den Raum, dessen Temperatur ermittelt werden soll,
hineinragen, daß es jenes Porzellangefäß tragen und dem Industriellen stets zur Hand
seyn muß, läßt es rathsam erscheinen, ein eisernes Rohr von hinreichender Stärke
anzuwenden.
Auf dieses Rohr ist zunächst das Hauptaugenmerk zu richten. Die darin enthaltene Luft
hat eine Temperatur, welche von dem Gefäß gegen das Manometer hin abnimmt. Es war
daher nöthig, das Volumen dieser Luft so weit zu vermindern, daß es im Vergleich mit
dem Volumen der in dem Porzellangefäß befindlichen Luft ohne bemerkbaren Fehler
vernachlässigt werden darf. Die Form des Gefäßes A ist
die eines von zwei Halbkugeln begrenzten Cylinders. Die eine dieser Halbkugeln geht
in einen cylindrischen Hals B aus, wodurch das Gefäß ein
flaschenähnliches Aussehen erhält. Der Hals ist an seinem Ende durch eine Flantsche
verstärkt. Der innere Rauminhalt des Gefäßes nebst Hals beträgt circa 290 Kubikcentimeter. Dem eisernen Rohr wurde eine
Länge von 1,5 Met. gegeben, welche für die meisten Fälle genügend erscheint, seine Bohrung hatte 1/2
Millimeter Durchmesser. Man verschafft sich diese capillare Bohrung, indem man in
ein eisernes Rohr einen genau anschließenden Cylinder treibt, in dessen Oberfläche
vorher, parallel zur Achse, eine Furche, welche die fragliche Bohrung abgeben soll,
geschnitten worden ist. Der Rauminhalt der letzteren betrug demnach ungefähr 1,2
Kubikcentimeter,Dieser Rauminhalt würde bei 1,5 Met. Länge einer cylindrischen Bohrung nicht
von 1/2, sondern von 1 Millimeter Durchmesser entsprechen.A. P. ein Volumen
welches ohne Zweifel bei der praktischen Messung außer Acht gelassen werden darf,
wodurch die Formel, durch deren numerische Berechnung man die Temperatur erhält,
sehr vereinfacht wird. Man kann eine Tabelle entwerfen, welche unmittelbar die
Temperatur als Function des beobachteten manometrischen Druckes darstellt.
Fig. 21 zeigt
die Verbindung zwischen der Porzellanstasche A und dem
Rohre. Letzteres besitzt an seinem Ende eine Erweiterung mit einem hohlen Raum, der
dazu bestimmt ist, den Hals der Flasche aufzunehmen. Dieser Hals endigt sich in eine
Flantsche, gegen welche ein kleiner eiserner Ring mittelst einer Schraube angepreßt
wird. Letztere besteht aus zwei Hälften, welche besagten Hals umfassen. Zwischen die
ebene Endfläche des Halses und den Boden des hohlen Raumes der Rohrerweiterung, und
eben so zwischen die Flantsche des Halses und die eiserne Schraube kommt eine
Asbestpackung zu liegen, so daß also auf diese Weise eine vollkommen luftdichte
Verbindung hergestellt ist.
Die Verbindung des eisernen Rohres mit dem Manometer wird, wie bei dem Thermometer
von Regnault mittelst eines doppelten Kegels
bewerkstelligt. Fig. 19 stellt diese Anordnung dar. Die mit dem besagten Rohr in
Verbindung stehende Manometerröhre ist von einem Glascylinder F umhüllt, welcher mit Wasser von der Temperatur der Umgebung gefüllt ist,
um jedem möglichen Einflusse der Wärmetransmission von dem Eisenrohr nach der Luft
der Manometerröhre, von dieser nach dem Quecksilber, und vermöge der
Leitungsfähigkeit des letzteren nach der Luft in der geschlossenen Manometerröhre
vorzubeugen. Beide Manometerröhren stehen mit einander und mit einem kleinen,
Quecksilber enthaltenden Röhrenansatz H (Fig. 18 und 20) in
Verbindung. Diese Verbindung läßt sich mit Hülfe eines Dreiweghahnes verändern.
Das Quecksilber des Röhrenansatzes H kann mit Hülfe eines
Kolbens, der sich auf- und niederschrauben läßt und mit einer
quecksilberdichten Packung versehen ist, in die Röhren gedrückt werden. Zwei Hähne
gestatten beide Röhren
mit der äußeren Luft in Verbindung zu setzen. Einer dieser Hähne kann zum Trocknen
der in dem Gefäße A enthaltenen Luft nach Regnault's Methode benutzt worden.
Oeffnet man die Röhren, so läßt sich in beiden das Quecksilber auf den Nullpunkt
bringen. Schließt man sie nachher und setzt den Apparat in Thätigkeit, so wird man
immer, indem man den Kolben bei zunehmendem Drucke allmählich in die Höhe schraubt,
das Quecksilber in der mit der Flasche A communicirenden
Röhre auf Null halten und auf der anderen Röhre die Manometerhöhe ablesen können.
Soll der Apparat transportirt werden, so läßt man alles Quecksilber in den Behälter
hinablaufen und sperrt dann die Verbindung zwischen dem Behälter und den Röhren
durch einen geeigneten Hahn ab. Auf diese Weise befindet sich der Apparat stets in
gebrauchsbereitem Zustande. Die Säule zwischen beiden Manometerröhren ist in
Millimeter getheilt. Durch die Reduction des Luftvolumens in der geschlossenen Röhre
wird der Druck angezeigt.
Bezeichnet V den Rauminhalt der Flasche A nebst Hals bei 0°, x die Temperatur, auf welche sie über die Temperatur der Umgebung erhitzt
wird, K den kubischen Ausdehnungscoefficienten des
Porzellans, dessen Werth als Mittel aus mehreren Bestimmungen = 0,00004 angenommen
werden kann, T die absolute Temperatur der Umgebung, P den barometrischen Druck und P¹ den manometrischen Druck, so hat man, indem man den Einfluß des
eisernen Rohres unberücksichtigt läßt, dem Elasticitätsgesetz der Gase gemäß
Textabbildung Bd. 210, S. 258
woraus
Textabbildung Bd. 210, S. 258
Würde man T = 300° annehmen und den in Atmosphären
ausgedrückten Werth P¹ = 7 setzen, ein Werth, der
einer Temperatur von circa 2000° entspricht, so
hätte der Ausdruck KP¹T den numerischen Werth 0,084, während P = 1
ist oder der Einheit möglichst nahe kommt. Daher kann man mit einem Fehler, der
kleiner als 1/10 ist, der obigen Formel folgende äußerst einfache substituiren:
Textabbildung Bd. 210, S. 258
Bezeichnet man unter Zugrundelegung der 100theiligen Scale mit X
die zu ermittelnde Temperatur, mit t diejenige der
Umgebung, und mit α den Ausdehnungscoefficienten
des Gases, so ist
Textabbildung Bd. 210, S. 259
Dieser Ausdruck läßt sich leicht aus der bekannten Fundamentalformel
Textabbildung Bd. 210, S. 259
welche die Beziehung zwischen den Voluminen V und V¹
eines und desselben Gases, ihren bezüglichen Temperaturen t und t¹ und
den Drücken P und P¹ darstellt, ableiten. Indem man nämlich, wie es der
vorliegende Fall verlangt, V¹ = V setzt, geht diese Formel zunächst in die
einfachere Relation
Textabbildung Bd. 210, S. 259
über. Durch Transformation dieser Verhältnisse erhält
man
Textabbildung Bd. 210, S. 259
und hieraus ergibt sich, indem man X statt t¹
setzt:
Textabbildung Bd. 210, S. 259
A. P.
Tafeln