| Titel: | Construction der Perkins'schen Wasserheizung; von C. Schinz. |
| Fundstelle: | Band 219, Jahrgang 1876, S. 331 |
| Download: | XML |
Construction der Perkins'schen Wasserheizung; von C. Schinz.
Mit Abbildungen auf Texttafel A.
(Fortsetzung von S. 219 dieses Bandes.)
Schinz, über Construction der Perkins'schen
Wasserheizung.
Circulation des Wassers in den
Röhren.
Wenn man bedenkt, wie wenig die Praktiker die Circulationsgeschwindigkeit des Wassers
in den Röhren beachten, so muß man sich billig wundern, wenn nicht alle ihre Anlagen
fehl schlagen und unbrauchbar sind, denn es kann sich nur sehr selten ereignen, daß
von ungefähr die richtige Geschwindigkeit erhalten werde, und gewiß in den meisten
Fällen ist sie entweder zu groß oder zu klein.
Da dieser Gegenstand von so großer Wichtigkeit ist, so wollen wir uns einläßlich mit
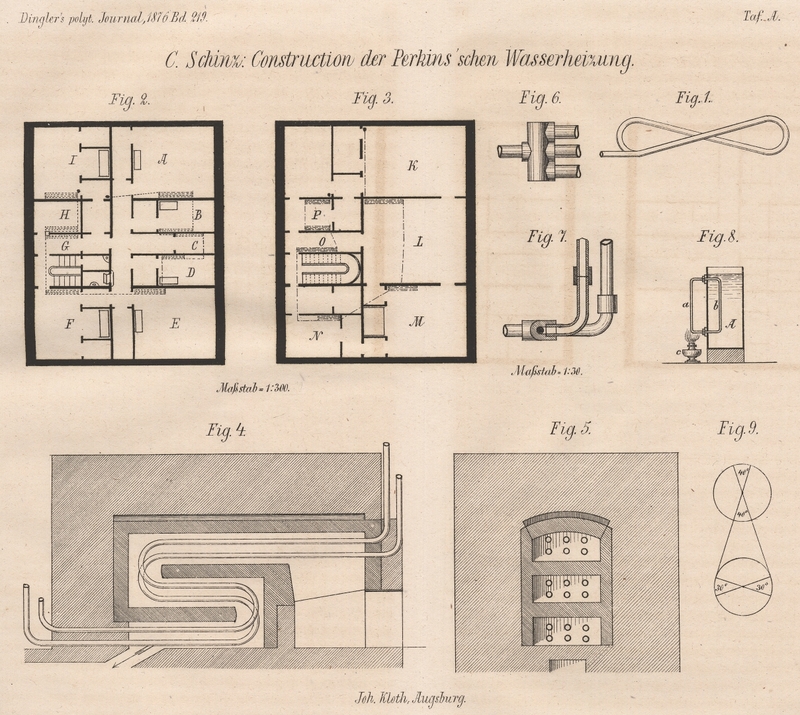
demselben beschäftigen. In Figur 8 repräsentirt A ein mit Wasser gefülltes Gefäß, a und b eine Perkins'sche Röhre, welche an der
äußern untern Biegung durch eine Weingeistlampe c
erwärmt wird. Dadurch wird das Wasser in der Röhre a
leichter als das in der Röhre b, und zwar um so
leichter, je höher dessen Temperatur steigt. Ist nun das Wasser in a leichter als das in b, so
fällt das Wasser in b und kommt an die Stelle, wo die
Lampe stets neue Wärme an das Wasser abgibt, während das wärmere Wasser nach b gedrängt wird, um von dem diese Röhre umgebenden
Wasser wieder abgekühlt zu werden. Ist s das specifische
Gewicht des heißen, s' das specifische Gewicht des
kalten Wassers, und es seien die Temperaturen = 60° und 0°, so werden
die Werthe von s und s' =
0,97279 bezieh. 1, und es ist, als ob das kältere Wasser im freien Raume um die
Differenz 1 – 0,97279 = 0,02721 fallen würde. Daher nach den Gesetzen des
Falles die Geschwindigkeit v = √2gp = √(2g × 0,02721) = 0m,73 wird,
wenn die Röhren die Höhe von 1m haben.
Hätten aber die Röhren die senkrechten Höhen von 2, 3, 4, 5m, so wären diese Höhen mit der Differenz
s' – s zu
multipliciren, und die Geschwindigkeiten würden 1,033 1,265 1,461 und 1,575, wenn
nämlich keine Reibungen, die der Strömung Widerstand leisten, vorhanden wären.
Es nimmt also die Geschwindigkeit mit der Höhe der Röhren zu, aber auch die
Temperaturdifferenz hat auf dieselbe Einfluß. Bleiben wir bei der Temperatur
0° für s' und machen dann bei 1m Höhe:
t =
60
70
80
90
100,
so sind die Differenzen s' –
s
0,97279
0,96841
0,96405
0,95975
0,95548
–––––––
–––––––
–––––––
–––––––
–––––––
0,02721
0,03159
0,03595
0,04025
0,04452,
woraus v =
0,731
0,787
0,840
0,888
0,934.
Ob die Röhre b durch Wasser oder durch Luft abgekühlt
werde, bleibt sich ganz gleich; nur könnte in einem so kleinen Apparate die Luft
nicht hinreichend abkühlen, um eine bemerkbare Circulation zu bewirken.
Bei den Perkins'schen Heizapparaten werden die Röhren stets von der Luft abgekühlt
und müssen zu diesem Ende eine ziemlich bedeutende Länge haben. Das vom Ofen
ausgehende Rohrstück wird immer wo möglich senkrecht an den höchsten Punkt der
Heizung geführt und heißt das Steigrohr, dagegen können dann die Transmissionsröhren
in allen Richtungen gehen und werden von dem Punkte an, wo sie hinreichend abgekühlt
sind, wieder in den Ofen zurückgeführt. Sind zwei oder mehrere Steigröhren
vorhanden, so hat man dem entsprechend auch mehrere Rückführungsröhren. Diese werden
nicht in dasjenige Ofenrohr geführt, von welchem das Steigrohr ausgegangen, sondern
in ein anderes. Dadurch wird die Circulationsgeschwindigkeit in allen Röhren gleich,
und die zu großen Widerstände des einen Systems werden durch die geringern eines
andern aufgehoben. Freilich sind daran noch zwei andere Bedingungen geknüpft, welche
von der Empirie gänzlich ignorirt werden. Es muß nämlich dann auch die Temperatur
des zurückgeführten Wassers dieselbe sein, und damit dieses stattfinde, ist dann
ferner erforderlich, daß alle Transmissionsröhren gleich lang seien.
Wäre z.B. eine der Transmissionsröhren so kurz, daß das Wasser aus derselben mit
100° in den Ofen zurückkehren würde, so wäre dann die Progression der
Temperaturen des Wassers im Ofen = 100 130 160 190 und 220, und wir hätten Kohle =
15k, W⁰ = 19,488 und w = 79,956.
Wärmevorrath.
T
t
T – t
Absorpt.
Ofen.
Summe.
112630
1400
220
1180
22996
7276
=
30272
82358
1030
190
840
16370
5717
=
22087
60271
754
160
594
11576
4158
=
15734
44537
557
130
427
8321
2599
=
10920
33617
420
100
320
6236
1040
=
7276
–––––––––––––––––––––––––
27341
342
65499
+
20790
=
86289
Somit würde die Transmissionsröhre, die im Ofen Wasser von
100° empfängt, um nahezu 2000c zu
wenig erhalten.
Um nun aber auf unser eigentliches Thema, auf die Circulationsgeschwindigkeit
zurückzukommen, haben wir anzugeben, wie dieselbe ermittelt wird, wenn den
Widerständen Rechnung getragen werden soll, welche das Wasser in den Röhren
erfährt.
Diese sind nun von zweierlei Art, nämlich Reibung an den Röhrenwänden und
Umbiegungen; die Reibungs- und Umbiegungscoefficienten sind ganz dieselben
wie diejenigen für Luft und Gase, nämlich K =
Reibungscoefficient = 0,024 und B = Widerstand durch
Umbiegung des Stromes = p, wenn diese im scharfen
rechten Winkel stattfindet, und = 1/2 p, wenn dieser
Winkel abgerundet ist.
Daher wird die effective Geschwindigkeit gefunden durch:
Textabbildung Bd. 219, S. 333
und, da zufällig D = K = 0,024 ist, so haben wir ganz einfach
Textabbildung Bd. 219, S. 333
Wenn also der Apparat Fig. 8
L = 3 und B = 4 hätte, so
würde bei t = 0 und t = 60
die effective Geschwindigkeit nicht 9m,73
sein, sondern
Textabbildung Bd. 219, S. 333
Welchen Einfluß hat nun die Geschwindigkeit auf die Leistung, auf den Erfolg des
Heizapparates? Wer dieses nicht bestimmen kann, der tappt im Dunkeln und wird auf
Erfolg nie rechnen können.
Und doch ist die Sache sehr einfach. Multipliciren wir die Geschwindigkeit mit dem
innern Querschnitte der Röhre, so haben wir das Volum des Wassers, das per Secunde
vorgeschoben wird; multipliciren wir dieses erste Product mit 1000, so haben wir das
Gewicht desselben (in Kilogramm); multipliciren wir dieses mit der
Temperaturdifferenz zwischen dem Wasser, welches aus dem Ofen aufsteigt, und dem
Wasser, welches in den Ofen zurückkehrt, so erhalten wir den Wärmegehalt dieses
Gewichtes; und multipliciren wir dieses endlich mit der Zahl der Secunden für eine
Stunde, nämlich 3600, so erhalten wir die Wärmemenge, welche die Transmissionsröhren
den zu beheizenden Räumen zuführt, und diese muß gleich sein dem Bedarfe.
Dieser Bedarf muß also gleich sein = v × Q × 1000 × (t'' – t') × 3600.
Wollen wir aber wissen, wie groß v sein muß, um dem
Wärmebedarf zu genügend, so haben wir
Textabbildung Bd. 219, S. 334
In unserm vorangestellten Projecte ist der Wärmebedarf 67447c, t'' = 250,
t' = 60, daher t''
– t' = 190, und wir haben
Textabbildung Bd. 219, S. 334
Da aber zwei Systeme sind, von welchen jedes die Hälfte dieser Leistung liefert, so
ist die Geschwindigkeit in beiden = 0,2182/2 = 0m,1091.
Um nun aber diese Geschwindigkeit effectiv zu erhalten, ist eine gewisse Druckhöhe =
P erforderlich, die sich nach folgender Weise
bestimmen läßt:
P = v²R/2g, wo
R die Reibungswiderstände repräsentirt.
Für die Differenz t'' – t' = 190° ist der mittlere Transmissionscoefficient W nach Tabelle II = 212,5. Dividiren wir diesen in die
vom System geforderte Leistung, so erhalten wir die nothwendige und richtige Länge
der Transmissionsröhre = 33723/212,5 = 158m, ferner 33723/3168 = ca. 10m
Ofenröhre und dazu 20m Leitungsröhren, so
wird dann der Widerstand durch Reibung = 158 + 10 + 20 = 188m, durch Umbiegungen, die wir vorläufig zu
100 annehmen wollen, = B/2 = 100/2 = 50. Daher ist dann
R = 1 + 188 + 50 = 239. Somit wird
Textabbildung Bd. 219, S. 334
Nun kennen wir zwar die Druckhöhe, aber noch nicht die Fallhöhe, d.h. die Höhe, von
welcher das auf 60° abgekühlte Wasser sinken muß, um jenen dynamischen Effect
zu erreichen. Diesen erhalten wir, wenn wir die Differenz der specifischen Gewichte
des Wassers in P dividiren; dieses Gewicht ist laut
Tabelle III s = 0,97279 für t' = 60° und s' = 0,89565 für t'' = 250°, daher ist die Fallhöhe
Textabbildung Bd. 219, S. 334
Wäre die Disposition des Apparates so, daß wir diese Fallhöhe nicht disponibel
hätten, so müßte man dann das System kürzer machen und dadurch den Widerstand
vermindern. Z.B. 10000/212,5 und 10000/3168 gibt 47m und 3m Röhren plus 20m Leitungsröhren
= 70m und Umbiegungen 50/2 = 25, macht dann
R = 1 + 70 + 25 = 96.
Daraus P = (0,1091² × 96)/2g = 0,0583 und daraus h =
0,0583/0,07714 = 0m,775.
Wäre im Gegentheile die disponible Fallhöhe größer als 1m,8805, so könnte das System noch länger
gemacht werden. Hätten wir z.B. eine disponible Fallhöhe von etwas mehr als 3m, so würden wir setzen 67000/212,5 und
67000/3168, welche 316m und 21m plus 20m Leitungsröhren geben; R würde dann ungefähr = 1 + 357 + 60/2 = 388, wenn wir
alle unnöthigen Umbiegungen vermeiden.
Daraus P = (0,1091² × 388)/2g = 0,2355 und dann h =
0,2355/0,07714 = 3m,05.
Es kommt aber auch vor, daß man mehr Fallhöhe hat, als man brauchen kann, und doch
nicht in der Lage ist, den Ofen höher zu setzen; dann würde die Geschwindigkeit der
Circulation zu groß werden und sich das Wasser nicht mehr genügend abkühlen können.
Dadurch wird aber die Differenz s – s' kleiner und alle Verhältnisse ändern sich dann.
Beispielsweise würde t'' = 250 und t' = 100, dann wird nach Tabelle II W = 251,8.
Dieses wird erhalten, wenn man die Werthe Ca von 101,7 an addirt und durch 15 dividirt. Danach würde dann die Länge
der Transmissionsröhre kleiner, oder sie würde 316 × 251,8 = 79569c statt 67000c transmittiren.
In diesem Falle wird dann die Geschwindigkeit
Textabbildung Bd. 219, S. 335
Dies würde der Erfolg sein, wenn besondere Verhältnisse eine so große Fallhöhe bieten
würden; ähnliches findet aber statt, auch wenn nur ein geringerer Ueberschuß an
Fallhöhe vorhanden ist. Der Erfolg ist nicht der, welchen man erwartet oder
beabsichtigt.
Es muß daher ein Mittel gefunden werden, durch welches wir eine zu große
Geschwindigkeit verhindern können. Zu diesem Ende sollte wohl der von Praktikern
empfohlene Regulirhahn dienen, denn Fallhöhe oder Druckhöhe könnte ein solcher nicht
geben. Ich habe die Wirkung eines solchen Regulirhahnes eingehend studirt und mich
überzeugt, daß ein solcher seinen Zweck unmöglich erreichen kann, weil es an allen
und jedem Kriterium fehlt, nach dessen ein solcher gerichtet werden könnte, und weil
schon 0mm,5 Tiefe der Täuschung eine sehr
bedeutende Aenderung in einem Querschnitte von blos 0qm,000452 macht.
Weit sicherer und vollständiger wird man den Zweck erreichen, wenn man in der Röhre
eine bleibende Hemmung anbringt, die a priori so
berechnet ist, daß sie gerade den vorhandenen Ueberschuß an Druckhöhe = P aufhebt. Hätten wir zum Beispiel für P = 0,2 nothwendig, aber durch eine Fallhöhe von 3m effectiv: (s
– s') h = 0,07714
× 3 = P = 0,2314, so müßte also eine Hemmung
angebracht werden, welche 0,0314 Druckhöhe absorbirt. Zu diesem Ende ist es am
besten, in der Rückführungsröhre eine kleinere Röhre einzuschieben, am besten eine
messingene Röhre, die an einem Ende mit einem hervorragenden Rand versehen ist,
welcher durch die Muffe zwischen zwei Röhren eingeklemmt wird. Dadurch findet dann
eine Contraction der Wasseradern statt, die je nach dem Verhältniß der Durchmesser
D und d der eisernen
Röhren und der Messingröhre mehr oder weniger Druckhöhe absorbirt.
Haben nun D und d die
angegebene Bedeutung, ist P' die absorbirende Druckhöhe,
v die Geschwindigkeit, also 0,1091 und A der Contractionscoefficient, der für Wasser = 0,625
ist, so finden wir:
Textabbildung Bd. 219, S. 336
Jeder Mechaniker, der Präcisionsinstrumente macht, ist im Stande, solche Röhren
herzustellen, welche das richtige Kaliber, in diesem Falle also 11mm,25 besitzen. Es ist natürlich
nothwendig, daß dieses Kaliber genau inne gehalten werde; denn wäre d = 0,012, so würde P' =
0,051 × v² + D⁴ (1/A⁴d⁴ – 1/D⁴) = 0,024256
sein, also schon 1,6 mal weniger, als wir wünschen.
Schon durch Betrachtung der Formel
Textabbildung Bd. 219, S. 336
ergibt sich, daß alle Verhältnisse sich am vortheilhaftesten
gestalten, wenn die Differenz t'' – t' möglichst groß ist. Wir müssen uns daher fragen, ob
nicht eine noch größere Differenz zur Anwendung gebracht werden könne?
Natürlich kann diese Differenz größer gemacht werden dadurch, daß man das Wasser
einerseits mehr erhitzt und anderseits mehr abkühlt. Der Transmissionscoefficient
für t = 65 ist 46c. Wenn wir also wie in unserem Projecte 8m,35 Röhren brauchen, um das Wasser von 70
auf 60° abzukühlen, so gibt uns diese Röhrenlänge 8,35 × 46 = 384c. Rechnen wir per Jahr 400 Heizstunden, so
macht dies 400 × 384 = 153600c oder
153600/6000 = 25k,6 Steinkohle im Jahre,
die etwa 0,8 M. kosten, während die 8m,35
Röhren ca. 22,5 M. kosten, was an Zu- und Abgang jährlich wohl 2,25 M.
ausmacht. Es ist also damit bereits das ökonomische Stadium überschritten, und eine
Compensation findet nur dann statt, wenn die Kaminhöhe uns wirklich erlaubt, die
Gase auf 100 statt 300° abzukühlen, in welchem Falle die 400 Heizstunden uns
hinwiederum eine Ersparniß von 400 × 1006c, entsprechend 67k Steinkohlen
geben. Betrachten wir ferner, wie schleppend es ist, große Röhrenlängen zu haben,
deren Transmission nur klein ist, so kommen wir ebenfalls zu dem Schlusse, daß die
Abkühlung auf 60° nicht ohne Nachtheile überschritten werden kann.
Ganz anders verhält es sich mit der Erhöhung der Temperatur des Wassers. Nach Perkins eigenen Beobachtungen hat die Initialtemperatur
des Wassers in seinen von ihm construirten Apparaten zwischen 450 und 560° F.,
was 232 und 293° C. ausmacht, gewechselt. 230, 260 und 290°
entsprechen den Drücken von 27, 38 und 73at. Ferner können Röhren von diesen Temperaturen unmöglich Holz entzünden;
dazu braucht es wenigstens 425°. Dann ist das Eisen, aus dem diese Röhren
gefertigt werden, nothgedrungen vom allerbesten Eisen, welches erst bei einer
Belastung von 60k pro 1qmm Querschnitt reißt, und da die
Rohrwandungen 12mm,5 Dicke haben, so wird
also die Röhre erst aus einander gehen, wenn auf 1qmm ein Druck von 12,5 × 60 = 630k kommt. Nun ist der Druck pro 1at und 1qmm = 0k,01033, also 38at = 0k,39254 und 73at = 0k,75409. Somit ist die Sicherheit gegen das
Bersten der Röhren im einen Falle eine 1605 fache, im andern Falle eine 836 fache.
Stiege auch die Temperatur der Röhren wirklich bis 425° der
Entzündungstemperatur von Holz, so wäre dann der Druck = 406at, der Druck pro 1qmm = 4k,19398 und die Sicherheit noch 150 fach. Es kann also in dieser Beziehung
durchaus kein Bedenken stattfinden, die Temperatur des Wassers wenigstens auf
denjenigen Grad zu bringen, den Perkins im Maximum
gegeben hat, nämlich 290° wodurch dann t''
– t' = 230° wird.
Dadurch würde dann der mittlere Transmissionscoefficient W, wie Tabelle II zeigt, bis auf 270,8 gesteigert werden können. Wollte
man dagegen bei 290° Initialtemperatur das Wasser nur auf 100°
abkühlen, so würde dann W = 419,3 und t'' – t' =
190°. Es sind also vielerlei Combinationen möglich, welche sich ein
geschickter Constructeur zu Nutzen ziehen wird, um allen Umständen Rechnung zu
tragen.
Wir wollen einmal diese letzte Combination für unser Project durchrechnen, und dann
sehen, ob und welche Vortheile sie uns über die angenommene gewährt.
Die Länge der Transmissionsröhren pro System wird dann = 33724/419,3 = 80m
Diejenige der Ofenröhre =
33724/3168
10
und benützen wir diesen Anlaß, um alle Röhren in den Boden zu
legen, so werden wir wohl höchstens an
Leitungsröhren
20
somit 110m Röhren
bekommen und nicht mehr als 30 Umbiegungen im rechten abgerundeten Winkel. Dadurch
wird dann der Widerstand R = 1 + 110 + 30/2 = 126.
Die nöthige Circulationsgeschwindigkeit
Textabbildung Bd. 219, S. 337
Die nöthige Druckhöhe P = v²R/2g = (0,10899² × 126)/2g = 0,07632 und endlich die erforderliche Fallhöhe = P/(s – s') = 0,07632/(0,95548 –0,88095) = 1m,024.
Findet dagegen die Anordnung so statt, wie wir sie
in unsern Plänen Fig. 2 und 3
verzeichnet haben, so sind die Widerstände in den 318m
Transmissionsröhren
318m
für Leitungsröhren im obern Stocke Fig. 3
23
für Leitungsröhren im untern Stocke Fig.
2
31,5
für 2 Steigröhren à
5,57
11
für 2 Rückführungsröhren à
5,9
12
für Ofenröhren à
23,22
46,5
–––––
Totale Röhrenlänge in Meter
442,0
An Umbiegungen im abgerundeten rechten Winkel, haben wir
für oben ausgezählte Spiralen (Fig. 1)
103 × 4
412
für Verbindung derselben mit Steig- und
Rückführungsröhren
21
im Ofen 4 doppelte Umbiegungen
8
4 scharfe Umbiegungen im rechten Winkel zur Vereinigung der
Röhren
8
––––
Summe der Umbiegungen
449.
Somit sind die Widerstände pro System
Textabbildung Bd. 219, S. 338
Dann ist
Textabbildung Bd. 219, S. 338
die erforderliche Fallhöhe
Textabbildung Bd. 219, S. 338
Wir haben also
R
v
P
h
Röhrenlängen
im ersten Falle
126
0,10899
0,07632
1,024
110m
im zweiten Falle
333,75
0,10899
0,20216
2,622
221m
Nun sind aber in der Wirklichkeit weder diese berechneten Druckhöhen P noch diese Fallhöhen h
vorhanden, und wir haben zu untersuchen, wie groß dieselben effectiv sind.
Bestimmung der effectiv vorhandenen
Druckhöhen.
Die in den Figuren repräsentirte Construction habe ich gewählt, nicht um ein Muster
dessen zu geben, was etwa am besten wäre, sondern um ein etwas complicirtes Beispiel
zur Bestimmung der Druckhöhe zu bekommen, die in solchen Fällen den Uneingeweihten
schwer erscheint.
Die Steigröhre fängt eigentlich schon am niedrigsten Punkte des Ofens an, da das
Wasser schon im Ofen in den 0m,33 hohen
Umbiegungen steigt; aber das Wasser hat nicht in der ganzen Steighöhe dieselbe
Temperatur.
Bei den ersten Umbiegungen hat t – t' = 120 – 60, bei der zweiten t – t = 174 –
120, daher entstehen die negativen Druckhöhen;
t' = 60
s = 0,97279
t = 120
s = 0,94704
= 0,02575 × 0,33
= 0,0084975
t = 120
s = 0,94704
t = 174
s = 0,92500
= 0,02204 × 0,33
= 0,0072732
–––––––––––
Zusammen P'
= 0,0157707.
Nun gehen beide Steigröhren bis auf den Boden des obern Stockes, die
Transmissionsröhren des ersten Systems kühlen sich auf demselben auf 60° ab
und kehren dann von dort in den Ofen zurück, dadurch wird eine Druckhöhe von
t' = 60
s = 0,97279
t'' = 250
s' = 0,89565
= 0,07714 × 5,9
= 0m,455126
erzeugt, indem das abgekühlte Wasser durch den ersten Stock,
der nebst Bodendicke 3m,1 Höhe hat,
hindurchfällt und dann noch durch das Kellergeschoß bis auf die Sohle des Ofens um
2m,8, zusammen 5m,9.
Von den Transmissionsröhren des zweiten Systems geben nur 9m,349 im obern Stocke 5785c ab (siehe oben Transmissionsröhren) und
kühlen sich dadurch von 250° auf 218° ab, nach der Proportion 33724 :
5785 = 190 : x, und geben dadurch, indem das Wasser mit
218° auf den Boden des untern Stockes sinkt, eine Druckhöhe von
t = 218
s = 0,90778
t'' = 250
s' = 0,89569
= 0,01209 × 3,1
= 0m,037479.
Im untern Stocke kühlten sich nun die übrigen Transmissionsröhren des zweiten Systems
auf 60° ab, und geben dann, indem das Wasser wieder auf die Sohle des Ofens
sinkt, noch eine Druckhöhe von
t' = 60
s = 0,97279
t = 218
s = 0,90778
= 0,06501 × 2,8
= 0m,182028.
Die Summe der erzeugten Druckhöhen ist also =
0,455126
0,037479
0,182028
––––––––
0,674633
und nach Abzug der negativen Druckhöhen
0,015771
––––––––
bleiben
0,658862/2
= 0m,3294311
Nun hatten wir oben
für t'' – t
= 290 – 100
P = 0,07632
für t'' – t'
= 250 – 60
P = 0,20216;
daraus ergibt sich, daß wir im erstern Falle einen Ueberschuß
an Druckhöhe von 0,2531111, im letztern von 0,1272711 haben. Zu bemerken ist jedoch,
daß im erstern Falle die effective Druckhöhe sich etwas modificirt, weil das Wasser
wärmer in den Ofen zurückkehrt; aber von großem Einflusse kann dies nicht sein.
Untersuchen wir nun, ob unter solchen Umständen es nicht möglich wäre, den Ofen statt
im Kellergeschoß in das untere Stockwerk zu setzen, wodurch dem Heizer die Mühe
erspart wäre, beim jedesmaligen Schüren in den Keller hinunter zu steigen, und was
den Vortheil hätte, daß der Ofen wohl aufmerksamer bedient und zugleich eine
Benützung der von ihm ausgegebenen Wärme gestatten würde.
In diesem Falle würde die erste gefundene Druckhöhe sich reduciren auf
0,07714 × 3,1 =
0,239289
die zweite bliebe dieselbe
0,037479
–––––––––
die dritte würde verloren gehen
0,276768
ab negative Druckhöhe
0,0157707
–––––––––
mittlere Druckhöhe
0,2609973/2
= 0,1304986 = P.
Es ließe sich also eine solche Versetzung des Ofens nur vornehmen, im Falle wir t'' – t = 290
– 100 machen; daher wären die Vortheile dieser Einrichtung einerseits
Reduction der Herstellungskosten auf etwa die Hälfte, und anderseits würde sie uns
erlauben, den Ofen dem Dienstpersonale näher zu bringen.
In diesem Falle haben wir noch einen Ueberschuß an Druckhöhe von 0,0541786 und im
andern einen solchen von 0,1272711.
Wir entledigen uns derselben durch Contractionsröhren von den Durchmessern
Textabbildung Bd. 219, S. 340
Ich denke das Vorstehende wird genügen, um in allen vorkommenden Fällen die effective
Druckhöhe zu ermitteln und die richtige Circulationsgeschwindigkeit herstellen zu
können, da sie sich wohl alle auf die angeführten Vorkommnisse zurückführen
lassen.
Möglichst große Differenzen t'' – t' und Vermeidung aller nicht absolut nothwendigen
Widerstände gegen die Circulation des Wassers sind die Ziele, die zu erstreben sind,
um wohlfeile Apparate herzustellen und um durch sichere Circulation des Wassers
Regelmäßigkeit zu erzielen und jede Gefahr zu beseitigen.
(Fortsetzung folgt.)
Tafeln