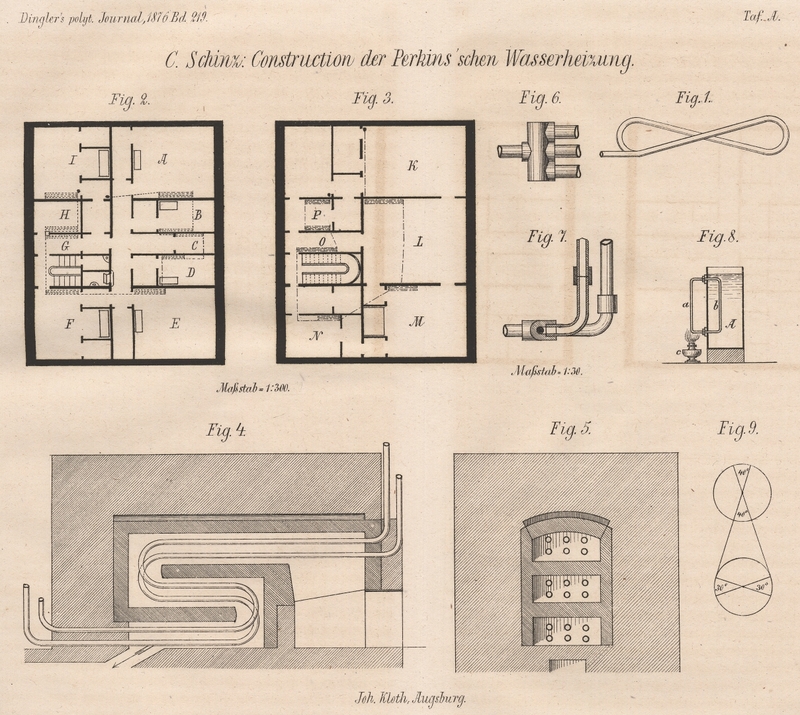
| Titel: | Construction der Perkins'schen Wasserheizung; von C. Schinz. |
| Fundstelle: | Band 219, Jahrgang 1876, S. 481 |
| Download: | XML |
Construction der Perkins'schen Wasserheizung; von
C. Schinz.
Mit Abbildungen auf Texttafel A.
(Schluß von S. 449 dieses Bandes.)
Schinz, über Construction der Perkins'schen
Wasserheizung.
Vortheile der
Hochdruck-Wasserheizung bei rationeller Construction.
Zur rationellen Construction gehört es nicht, wenn man jede Etage für sich beheizen
will, es wäre denn, daß diese eine Etage eine sehr große Ausdehnung hätte, wie
manche industrielle Arbeitshallen und namentlich Kirchen, da die
Wärmetransmission des Ofens selbst nur dann außer Berechnung kommt, d.h.
verschwindend klein wird, wenn recht viele Röhrensysteme in einem und demselben Ofen
zu erwärmen sind.
Sowohl in staatsökonomischer als privatökonomischer Rücksicht kann die
Hochdruckwasserheizung die größten Vortheile vor allen andern Heizsystemen bieten,
wenn dieselbe so angewendet wird, wie sie benützt werden sollte; sie kann sogar alle
andern Heizsysteme darin überbieten, indem sie die wohlfeilste ist, und durch deren
mögliche große Ausdehnung kann sie auch zu derjenigen werden, welche durchaus den
kleinsten Brennstoffbedarf fordert. Wir haben an dem Projecte, das ich
vorausgestellt habe, gesehen, daß ein ziemlich großes Haus mit 2 Röhrensystemen von
zusammen nur 318m Röhren beheizt werden
kann. Derselbe Ofen könnte auch 12 Röhrensysteme aufweisen, ohne deshalb bedeutend
mehr Wärme zu transmittiren und also auch gleichzeitig 6 große Häuser mit Wärme
versehen.
Bei den immer theurer und rarer werdenden Brennstoffen ist es sogar eine
staatsökonomische Frage: wie der öffentliche Vorrath desselben gespart werden könne?
Daher ist es wohl der Mühe werth, zu untersuchen, was durch diese Heizsysteme im
Vergleiche mit andern geleistet werden könne.
Als Typus der allgemein gebräuchlichen Heizapparate, namentlich in kältern Klimaten,
können wir den Kachelofen mit glasirter Außenfläche betrachten und Holz oder Torf
als dazu verwendete Brennstoffe.
Es ist nicht ganz leicht zu bestimmen, wie groß der Nutzeffect eines solchen
Apparates sei, da selbst während dem das Feuer im Ofen brennt, die Temperatur der im
Kamin entweichenden Gase stets wechselt, im Anfange wird viel, am Ende wenig Wärme
vom Ofen absorbirt. Doch compensiren sich diese Extreme während der Zeit, in welcher
das Feuer brennt. Ebenso ist die Absorption des Ofens weit größer, so lange die
inneren Wände noch kalt sind, als wenn sie bereits eine gewisse Temperatur erlangt
haben. Und in der Jahreszeit, wo täglich gefeuert wird, werden diese innern Flächen
gar nicht kalt. Daher kann eine Berechnung dieser Vorgänge nur eine Annäherung an
die Wirklichkeit geben.
Als Beispiel wähle ich einen runden Kachelofen, wie derjenige ist, von dem ich
gegenwärtig in meinem Studirzimmer Gebrauch mache, und den ich unter meiner Aufsicht
mit den nöthigen Vorsichtsmaßregeln beheizen lasse. Diese bestehen namentlich darin,
daß ich den Herd so stark als möglich mit Brennstoff füllen lasse, damit möglichst
wenig überschüssige Luft in denselben gelangen könne, und dann den Ofen verschließen
lasse,sobald das nöthige Quantum verzehrt ist. Dieses Quantum ist in kalten Wintertagen
20k Torf, die also in etwas mehr als
einer Stunde 20 × 3529 = 70 580c
produciren und den Gasen eine Initialtemperatur von 1213° geben.
Der Ofen hat 0m,554 äußern und 0m,25 innern Durchmesser, so daß also die
Thonmasse einen Ring von 0qm,192 bildet und
die Wanddicke 0m,152 beträgt. Der Ofen ist
1m,60 hoch. Ein Ringstück von 0m,10 Höhe enthält also 0,192 × 0,10
= 0cbm,0192 Thonmasse. Diese wiegt: 0,0192
× 1800 = 34k,56 und hat die
Wärmecapacität von 34,56 × 0,2 = 6c,912.
Die Temperatur der äußern Ofenwandfläche = τ' ist
bei der Initialtemperatur T' = 1213°:
Textabbildung Bd. 219, S. 482
τ = die Temperatur der Luft = 20°
S = Strahlungscoefficient für glasirte Fläche = 2,91
L = Leitungscoefficient = 2,05
e = Wanddicke = 0,152
C = Leitungsfähigkeit des Materials des Ofens = 0,6.
Wir bekommen
Textabbildung Bd. 219, S. 482
Wenn nun 493° die äußere und 1213° die innere Temperatur ist, so hätte
die Ofenwand eine Temperatur von 1/2(1213 + 493) = 853°; aber da die innere,
ja sogar die ganze Wand schon eine gewisse Temperatur besaß, ehe das Feuer
angezündet wurde, so bringen wir nur τ' in
Rechnung und multipliciren dieses mit der Wärmecapacität des Ofenstückes = 6,912,
was 3407° ergibt.
Ziehen wir nun diese absorbirten 3407c von
unserem Vorrathe = 70 580c ab, so bleiben
67 173c, und die Temperatur T der Gase wird 67 173/w .
w ist die Wärmecapacität der Gase = 20
× 2,90955 = 58,191, daher T = 1154, mit welcher
wir nun auf gleiche Weise die Absorption für das nächste Ofenstück von 0m,1 Höhe berechnen.
So bekommen wir dann folgende Reihe.
Wärmevorrath.
T
τ'
Absorbtionτ'
× 6,912
70580
1213
493
3407c
67173
1154
470
3248
63925
1098
449
3103
60822
1045
428
2958
57864
994
406
2806
55058
946
387
2675
52483
902
369
2550
49933
858
352
2433
47500
816
336
2322
45178
776
316
2184
42994
739
305
2108
40886
703
291
2011
38875
668
277
1914
36961
635
264
1825
35136
604
252
1742
33394
573
239
1652
––––––
31742
545
38948.
Um aber dieses Resultat vergleichbar zu machen, fragen wir, wie viele Wärmeeinheiten
aus dem Brennstoffe bedarf es, um 6000c
Nutzeffect zu haben. Das sind 6000 × 70580 : 38948 = 10873c, und daraus ergibt sich dann der
Nutzeffect: 6000 × 100 : 10873 = 55,18 Proc.
Für die Hochdruckwasserheizung brauchen wir für 6000c 1k Kohle, wenn die Gase mit 300° evacuirt werden. Wenn sich auch da
bei hohen Kaminen noch eine Ersparniß machen läßt, so bringen wir diese doch nicht
in Rechnung, um uns ja vor Illusionen zu bewahren. Mehrfache Berechnung zeigt, daß
man innerhalb der Grenzen der Wahrheit bleibt, wenn man annimmt, daß der Ofenconsum
für das Minimum der Leistung von 6000c
16000c betrage, und dann für je 1000c mehr 170c mehr. Nach dieser Progression erhalten
wir folgende Tabelle der erhältlichen Nutzeffecte.
Leistung.
Ofentransmission.
Consum.
Nutzeffect.
c
c
c
Proc.
6000
16000
22000
27,3
12000
16840
28840
41,6
18000
17260
35260
510
24000
17680
41680
57,6
30000
18100
48100
62,4
60000
20500
80500
74,5
120000
24400
144400
83,1
240000
38800
272800
88,0
360000
41200
401200
91,0.
Es wird also die Wasserheizung erst mit dem Kachelofen gleich kommen, wenn dieselbe
wenigstens 20000 bis 23000c zu leisten hat,
unter diesem Quantum ist dieser vortheilhafter.
Dagegen gibt die Wasserheizung mit Hochdruck Ersparnisse von
2,4
7,2
19,5
27,9
32,8
35,8
Proc., wenn sie für Leistungen von
24
30
60
120
240
360
Tausend Calorien zur Anwendung kommt.
Auch die Kosten der Darstellung der Kachelöfen sind geringer als die der
Wasserheizung, wenn man dieser nur eine mittlere Transmission von 100c pro 1m gibt, und wenn man die Röhren in dichte Spiralen aufwindet.
Wenn uns der Kachelofen pro Stunde 38948 : 12 = 3250c gibt, so haben wir für dieselbe Leistung
in Wasserröhren 3250 : 100 × 0,55 = 59m Transmissionsröhren plus 1/6 = 10m Ofenröhren zu nehmen, also 69m
Röhren, welche 184 M. kosten, während ein Kachelofen der angegebenen Größe kaum mehr
als 80 M. kosten wird.
Machen wir dagegen W = 331,4, so wird der Röhrenaufwand =
(3250 : 331,4) + (3250 : 2640) = 11m,
welche 30 M. kosten.
Die Wasserheizung mit niedrigem Drucke wäre für die Hochdruckheizung eine gefährliche
Concurrentin, wenn ihre Anlagekosten nicht bedeutend höher wären; denn sonst wird
sie als dasjenige Heizsystem angesehen werden müssen, welches den größten Nutzeffect
gibt, da der Ofen von einer solchen Construction ist, daß er gleichzeitig als
Zimmerofen gelten kann. Hingegen ist dann dieses Heizsystem ausschließlich nur dann
anwendbar, wenn nur eine Etage beheizt werden soll, verdient dann aber auch in
diesem Falle vor allen andern den Vorzug.Der vollkommenste Apparat dieser Art ist der in „Heizung und
Ventilation“ in den Fig. 106 bis 109 auf Taf. IX abgebildete
und S. 149 ff. beschriebene.
Die große Analogie dieses Apparates mit dem Hochdrucksysteme macht eine nähere
Vergleichung desselben interessant und daher wünschbar.
Da das Wasser von 20° auf 100° erwärmt wird, so ist der mittlere
Transmissionscoefficient:
Temperaturdifferenz der Luft
0
10
20
30
40
50
60
70
80
Temperaturdifferenz des Wassers
20
30
40
50
60
70
80
90
100
Coefficient pro 1qm
0
58,1
126,3
201,0
282,0
369,0
461,0
559
664
Mittlere Coefficienten
29,0
92,2
163,6
241,5
325,5
415,0
510,0
611,5
2388,3 : 8 = W = 298c.
Dieser scheinbar große Coefficient gilt aber für 1qm Oberfläche und nicht für einen laufenden Meter, wie die Coefficienten
der Tabelle I. Für solche Röhren wäre er nur 298 × 0,1414 = 42c.
Wenn nun unsere Transmissionsgefäße ebenfalls aus Röhren vom Durchmesser = 0m,2 bestehen, so ist der Coefficient pro
1m Röhrenlänge
= Wärmemenge/(0,2π ×
298)
Wärmemenge =
12000
18000
24000
30000
36000
42000
Länge der Transmissionsröhren =
64
96
128
160
192
224m.
Nun ist der Wassergehalt dieser Transmissionsgefäße =
L
× 0,068
× 0,068
× π
×
1000 =
236
355
473
591
710
828k
und deren Wärmegehalt = der Mittlern Temperatur dieses Wassers
von 40°, multiplicirt mit diesen Gewichten:
9440
14200
18920
23640
28400
33120c.
Sie enthalten also 79 Proc. der Wärme, die sie pro Stunde
abgeben sollen, und fahren also fort Wärme abzugeben, wenn das Feuer im Ofen
gelöscht ist. Dies ist ein Vortheil, welchen kein anderes Heizsystem in demselben
Maße gewährt, und welcher eine Regelmäßigkeit der Heizung hervorbringt, die sehr
werthvoll ist. Wem es also möglich ist, der wird wohl thun, diesen Vortheil auch bei
größern Anlagekosten sich zu verschaffen. Namentlich ist der Vortheil, am frühen
Morgen sehr bald die normale Zimmertemperatur wieder zu erhalten, ein
bedeutender.
Zur Bestimmung der Heizfläche, welche die Wärme des Feuers an das Wasser überträgt,
haben wir
1/2 [(T' + T⁰) – (t'' – t')].
Für Steinkohle
1/2 [(1400 + 300) – (100 – 20)] = 810 ×
59,3555, daher für die
Leistungen von
12000
18000
24000
30000
36000
42000
Heizfläche =
0,249
0,374
0,499
0,624
0,749
0,874qm.
Bei sehr großer Winterkälte, wo die Maximalleistung
stattzufinden hat, würden diese Heizflächen nicht ausreichen, um auch noch den oben
berechneten Wärmevorrath aufzuspeichern; aber ein geringer Ueberschuß an Brennstoff
würde solchem Uebelstande leicht abhelfen oder auch gar nicht nöthig sein, wenn die
Kaminhöhe genügt, um auch mehr abgekühlte Gase zu evacuiren.
So schön der citirte Ofen construirt ist, so möchte es doch kaum lohnen, denselben
nachzuahmen, da ein solcher zu theuer zu stehen kommt. Was hingegen nachzuahmen ist,
das ist die Führung der Flamme nach oben, um sie dann an den Heizflächen wieder nach unten zu
führen. Dazu kann eine feuerfeste Thonröhre eben so gut dienen, als eine mit Wasser
gefüllte. Es genügt, zwei mit Calotten endende Blechcylinder unten durch Flanschen
mit einander zu verbinden. Hat das innere einen Durchmesser von 0,56, so genügt für
den äußern ein Durchmesser von 0,70. Die Fläche des innern Cylinders wäre dann
0,56 π
× 0,15 + Calotte 0,56²π/2 =
0,757die der äußern 0,7π × 0,15 + Calotte 0,70²π/2 = 1,100
= 1qm,857
Blech würden dann für die erste der berechneten Heizflächen
genügen, auch würde eine Metalldicke von 2mm entsprechen, so daß das Gewicht derselben incl. Nieten und Flanschen
nur ca. 24k ausmachen würde. Die dadurch
gebotene Transmissionsfläche würde so nicht mehr kosten als die Transmissionsgefäße
von Guß.
Uebrigens ist es keineswegs nöthig, für jede Größe der Leistung einen andern Ofen zu
construiren, da ja aller Ueberschuß von Wärme aufgespeichert wird; daher wäre es
wohl rathsam, den Ofen immer so zu machen, als ob er für 42000c genügen müßte. Dazu ist ein Consum von
7k pro Stunde erforderlich; diese
verlangen eine Rostfläche von 0qm = 0m 35 auf 0m,20. Die Verbrennungsproducte haben bei
der Initialtemperatur pro Stunde das Volum von 0cbm,249 und geben wir denselben eine Geschwindigkeit von 1m,8, so wird der Querschnitt der thönernen
Röhre = 0,249 : 1,8 = 0qm,1385 und deren
innerer Durchmesser d √(0,1385/π) = 0m,42; der innere Blechcylinder d = 0,6 und dessen
Höhe bis zur Calotte = 0,874 : 0,67π = 0m,464.
Es würden dann pro Stunde 6000 × 7 = 42000c entwickelt und 0,979 Stunden = 59 Minuten Feuerung genügen, um 24000c zu transmittiren und 18 920c aufzuspeichern. Daher müßten bei diesem
Maximumbedarf nur etwa alle 2 Stunden 7k
Kohle verbrannt werden.
Ist der Transmissionscoefficient bei diesem Systeme außerordentlich klein, so sind
dagegen dann auch die Widerstände, die sich der Circulation des Wassers
entgegensetzen, ebenfalls außerordentlich klein. Die oben berechneten
Transmissionsröhrenlängen von 0m,2 äußerm
Durchmesser werden je nach der Höhe der Zimmer in Stücke von 2,6 bis 2m,8 Länge getheilt und senkrecht neben
einander gestellt. Theilen wir z.B. die 64m
Röhren zur Leitung von 12000° durch 2,7, so erhalten wir 24 Röhrenstücke von 2m,7 Länge und 0m,186 innerm Durchmesser, daher vom
Querschnitte 0qm,00363. Nun bewegt sich das
Wasser gleichzeitig in allen diesen 24 Röhrenstücken, also in einem
Gesammtquerschnitte von 27 × 0,00363 = 0qm,098. Dadurch würde die Geschwindigkeit 0,236 : 3600 × 0,098 =
0,0007, so daß dieselbe ganz außer Betracht kommt, indem sie so zu sagen keinen
Widerstand leistet. Dieser rührt blos von den Zu- und Ableitungsröhren her,
und von den Umbiegungen, Expansionen und Contractionen, welche das Wasser beim
Austritte und Eintritte in die Transmissionsgefäße erfährt. Aber auch selbst diese
Leitungsröhren dürfen wir nur für die Hälfte ihrer Länge in Rechnung bringen, da
dieselben über oder unter jedem Transmissionsgefäße nur einen Bruchtheil des Wassers
aufnehmen oder abgeben.
Wenn wir ferner auch aus diesen Röhren 27 Umbiegungen im rechten scharfen Winkel
haben, so ist doch nur eine dieser Umbiegungen in Rechnung zu ziehen, da die
Geschwindigkeit in denselben nur 1/27 der wirklichen Geschwindigkeit ist. Da nun
eine Umbiegung oben und eine unten stattfindet und dann noch eine abgerundete aus
dem Ofen und eine solche in den Ofen, so ist die Zahl, welche als Widerstand für
diese in Rechnung kommt, = 3.
Wenn aus den Leitungsröhren das Wasser in die Transmissionsgefäße gelangt, so findet
durch die Differenz der Röhrendurchmesser eine Expansion statt, die 0,08 beträgt;
beim Austritte hingegen findet eine Contraction statt, welche 0,49 beträgt, daher
reducirt sich der Widerstand dafür auf 2 (0,49 – 0,08) = 0,82.
Haben die Leitungsröhren einen innern Durchmesser von 0,02, so ist deren Widerstand =
KL/d; für die
Leitung 12000 soll die Länge L = 10m sein, so haben wir 0,024 × 10 :
0,02 = 12. Somit sind die Widerstände, wenn wir für die Leistungen
12000
18000
24000
30000
36000
42000
die Leitungsrohre annehmen
10
20
30
40
50
60m
für Reibung
12
24
36
48
60
72
für A – B + 1
1,82
1,82
1,82
1,82
1,82
1,82
für Umbiegungen
3
3
3
3
3
3
Summe R.
16,82
28,82
40,82
52,82
64,82
76,82.
Wenn nun der Ofen einen Ueberschuß von Heizfläche hat, um schnell Wärme
aufzuspeichern, so muß die Geschwindigkeit eine größere werden und zwar in dem
Verhältniß dieser Aufspeicherung
12000/9440 = 1,27
18000/14200 = 1,27
24000/18920 = 1,27
30,000/23640 = 1,27
36000/28400 = 1,27
42000/33120 = 1,27
Daher berechnet sich die Geschwindigkeit
(d = 0,02. Q = 0,000314. t'' – t' = 80°) durch
v = Wärmemenge/(Q × 1000
× 3600 × 80) × 1,27, und wir erhalten:
v =
0,1686 0,2529 0,3372 0,4215 0,5058 0,5901
Daraus berechnen sich die Druckhöhen P = v² R/2g, und wir haben
P =
0,02438
0,09399
0,2366
0,4785
0,8456
1,3640.
Wenn nun der Sockel des Ofens 0,8 und die Höhe der Heizfläche = 0,464, so wird das
Wasser nur von der Höhe 1m,664 ansteigen,
und wenn die Decke 2m,7 über dem Boden ist,
so kann die Vertheilungsröhre nur 2,7 – 1,664 = 1m,036 höher als die Heizfläche liegen,
daher kann auch die Fallhöhe des abgekühlten Wassers nur 1m,036 sein, und wir fragen, welches wird
die Temperatur des Wassers in den Transmissionsgefäßen auf dieser Höhe von der Decke
sein?
Jedes der Transmissionsgefäße hat oben 100° und unten 20°; Differenz =
80°. Daher wird auf die Höhe von 1,036 von der Decke die Temperatur 1,036
× 80 : 2,7 = 31° kleiner als 100° sein.
Daraus wird dann die effective Druckhöhe:
für
69 = 0,96886
100 = 0,95548
0,01338 × 1,036 = P = 0,01386.
Sie ist also für alle Fälle zu klein. Als Correctiv kann nur ein vergrößerter
Durchmesser der Leitungsröhren zur Anwendung kommen; geben wir diesen den
Durchmesser 0,05, so wird der Widerstand für L = 50, R = 28,82; daraus v = 0,0995
und P = 0,01454, also nur noch um 0,00068 zu groß. Man
wird also einfach durch Vergrößerung der Leitungsröhren die Druckhöhe derjenigen
anpassen können, welche die vorhandene Fallhöhe und Temperaturdifferenz gibt.
Für den Brennstoffconsum haben wir 1k Kohle
für 6000c in Rechnung zu setzen, wenn die
Verbrennungsproducte mit 300° im Kamin abziehen. Einen günstigern Effect
erhalten wir, wenn die Höhe des Kamins erlaubt, diese auf 200° oder
100° abzukühlen. Diese Ursache der Ersparniß kann auch bei der
Hochdruckheizung zur Anwendung kommen, daher wir sie zur Vergleichung nicht in
Anspruch nehmen dürfen. So würde dann der Nutzeffect dieses Apparates constant 80
Proc. betragen – auch dann, wenn er nur für eine Leistung von 6000 oder
12000c dienen soll, und insofern ist er
der Hochdruckheizung überlegen, da diese erst bei einer Leistung von 60000 bis
120000c diesen Nutzeffect gibt. Dagegen
sind dann die Anlagekosten bedeutend höher.
Für die Leistung des Kachelofens pro Stunde hatten wir
38 948 : 12 = 3245° pro Stunde.
Mit diesem Apparate brauchen wir 3245 : 298 = 10qm,9. Diese geben 10,9 : 0,2π = 17m,4 Transmissionsröhren, welche 17,4 × 51,65 = 896k, mit Flanschen und Schrauben rund 920k wiegen, zu 20 Pf. also 184 M. kosten
gegen 80 M. für Kachelofen, 102 M. für übliche Perkins'sche Röhren und 43 M. für
rationelle Construction.
Als nächster Concurrent der Hochdruckwasserheizung kommt nun die sogenannte
Luftheizung. Auf den ersten Blick sollte man glauben, daß die unmittelbare Erwärmung
der Luft nicht nur die größte Oekonomie im Betriebe, sondern auch in der Anlage
bringen würde. Dies wäre allerdings der Fall, wenn ganz richtig verfahren würde;
aber unsere Praktiker glauben sich sehr große Techniker, wenn sie im Stande sind,
etwa eines der vielen Probleme zu bemeistern, die da vorkommen und zu lösen sind,
und halten ihre Apparate für sehr gelungen, wenn es nur gelingt, die Räume so zu
erwärmen, wie es verlangt wird; ob dazu viel oder wenig Brennstoff gebraucht werde,
das ist ihnen ganz gleichgiltig.
Mit Recht beklagt man bei solchen Heizungen den Nachtheil, daß sie nur aller
Feuchtigkeit beraubte Luft liefern und dadurch dem Wohlbefinden der Bewohner so
beheizter Räume nachtheilig werden. Dennoch ist nicht das System dieser Heizung mit
diesem Fehler behaftet, sondern nur die fehlerhafte Ausführung derselben. Sobald die
zu erwärmende Luft rasch, d.h. mit einer gewissen Geschwindigkeit über die
Heizflächen hingleitet, so wird dieser Nachtheil beseitigt, besonders aber dadurch,
daß man der Luft als Träger der Wärme nur eine mäßige Temperatur gibt, – eine
Regel, welche zwar (glaube ich) jetzt allgemein befolgt wird.
Zur Erhebung der Leitung haben wir die benöthigte Quantität von Wärmeeinheiten durch
0,2669 (t' – t°) zu dividiren; d.h. die Temperatur t' = derjenigen, welche die Luft erhalten soll, t⁰ = derjenigen, mit der sie in den Ofen gelangt. 0,2669 ist die
Wärmecapacität von 1k Luft.
Wollten wir eine Luftheizung ausführen, welche das leistet, was in unserm
vorausgestellten Projecte für Perkins'sche Röhren gefordert wird, so hätten wir die
Luft mit 60° in die Zimmer ein- und mit 10° abzuführen, also
67000 : (60 – 10) 0,2669 = 502k =
652cbm Luft pro Stunde oder pro Secunde
0cbm,18116. Wenn die Temperatur in den
Zimmern = 20° sein soll, so wäre dann die Druckhöhe für die Canäle, wenn h = deren Höhe, h –
h × 0,84512. (Letzterer Werth ist gleich dem
specifischen Gewichte der Luft bei 50°, da die Differenz zwischen der
zugeführten und abgeführten Luft auch = 50° ist.) Die disponible Kraft wird
also immer eine sehr kleine werden, daher auch eine genaue Berechnung der statischen
Verhältnisse nothwendig. Auf diese will ich zwar hier nicht eingehen, da ich an
andern Orten dies bereits mit großer Ausführlichkeit gethan habe.
Glücklicherweise für die Constructeure solcher Apparate ist es nicht absolut
nothwendig, diese statische Berechnungen zu machen, da bei mangelnder Circulation
der Luft diese sich in der Heizkammer spannt und dadurch das Gleichgewicht wieder
herstellt, freilich auf Kosten des Brennstoffes und mit einer erhöhten
Eintritts- und Abführungstemperatur.
Ueberhaupt eignen sich diese Vorrichtungen eher für schmale aber hohe Localitäten, da
es selbst bei richtigster Berechnung unmöglich ist, auf eine richtige Vertheilung
der Wärme in die verschiedenen Räume zu zählen, wenn diese nicht über, sondern aus
einander liegen, da es den Bewohnern selbst überlassen bleiben muß, die
Zuflußregister zu öffnen und zu schließen, wenn wenigstens solche vorhanden sind;
und kein Constructeur würde es wagen, solche entbehrlich zu machen, indem er a priori die Größe der Ausflußöffnungen bestimmt. Bei
diesem Sachverhalts sollte dann aber doch wenigstens die nothwendige große Kaminhöhe
benützt werden, um die Verbrennungsgase mit einer möglichst geringen Temperatur in
dasselbe zu entlassen. Um aber dieses bewerkstelligen zu. können, ist erstens
unerläßlich, die richtige Heizfläche zu haben, und zweitens eine Ofenconstruction,
welche keinen bedeutenden Consum veranlaßt. Gegen beide dieser Regeln wird aber
vielfach gefehlt, indem man nach sogen. praktischen Regeln verfährt, welche gar
nicht für alle Einzelnfälle passen.
Approximativ erhalten wir die nöthige Heizfläche durch die Proportion
300 : 46 = 60 : F, woraus F = 9qm,2,
wenn nämlich die im Heizapparate erwärmte Luft mit 60°
Temperatur in die zu beheizenden Räume einströmen soll.
Ist der Wärmebedarf wie in unserm frühem Projecte = 67000c pro Stunde, so ist der approximative
Steinkohlenbedarf = 67000 : 6000 = 11k,166
Steinkohle.
Berechnen wir nun wie früher die Factoren für 4 Cylinder, so erhalten wir:
Wärmevorrath 11,166 × 7509 = 83844c.
Wärmecapacität der Gase w = 11,166 × 5,3305 =
59,52.
Temperatur der sich allmälig erwärmenden Luft, die mit 10° in den Heizapparat
gelangen soll und mit 60° aus demselben abgeführt wird,
10° 22,5° 35° 47,5° 60°.
Die von der Heizfläche pro Stunde transmittirte Wärmemenge
= W° ist 9,2 × 14,4 : 4
= 33c,12,
da 1chm für t' – t°=
1° pro Stunde 14c,4
transmittiren.
Wir haben somit
Wärmevorrath
T
t'
T – t'
c
83844
1408
47,5
1360,5
× W° =
45059
38785
652
35
617
20435
18350
308,5
22,5
286
9472
8878
149
10
139
4603
–––––
4275
71
79569.
Dieses Resultat zeigt uns, daß die berechnete Heizfläche zu groß ist, da sie uns
12569° zu viel liefert. Aber auch die Brennstoffmenge ist zu groß, denn
nehmen wir mehr davon, so wird die Transmission nur noch größer. Wir vermindern
daher allmälig die Werthe w und W°, bis wir die richtige Transmission und eine annehmbare
Evacuationstemperatur erhalten. So kommen wir zu 9k,7 Steinkohle, w = 51,706 und W° = 7,2 × 14,4 :
4 = 25,95.
Wärmevorrath
T
t'
T – t'
c
72837
1408
47,5
1360,5 × W° =
35304
37533
726
35
691
17931
19602
379
22,5
357
9264
10338
200
10
190
4930
–––––
5408
104
67429.
Nun wäre noch zu untersuchen, ob eine Evacuationstemperatur von 104° genüge,
um im Kamine hinreichenden Zug hervorzubringen. Dies wird kaum der Fall sein, wenn
die Höhe desselben gering ist, oder wenn den heißen Verbrennungsproducten große
Widerstände entgegenstehen, wie das z.B. bei der üblichen Construction dieser
Apparate der Fall ist, wo die Heizflächen aus Röhren gebildet werden, welche
mehrfach nach oben umgebogen sind, und in denen die Gase eine verhältnißmäßig große
Geschwindigkeit annehmen müssen.
Es sind diese Verhältnisse von größerer Wichtigkeit, als man gewöhnlich glaubt, denn
die Oekonomie hängt von denselben ab. Um z.B. eine hohe Evacuationstemperatur zu
erhalten, würde der Consum von 9k,7 auf
12k erhöht, die Heizfläche aber von 7,2
auf 5qm,5 reducirt, während die Empiriker
ihre Heizflächen wohl doppelt so groß machen, als zuträglich wäre, und dann
genöthigt sind, den Consum ebenfalls zu erhöhen. Dies ist aber nicht der einzige
Nachtheil, der daraus entsteht, sondern die zu erwärmende Luft wird dann statt auf
60° wohl auf 80 bis 100° erwärmt und dadurch die Circulation derselben
in den zu heizenden Räumen beeinträchtigt, was der Regelmäßigkeit sehr schadet.
Bei den gemachten Annahmen ist das pro Stunde circulirende Gewicht an Luft 67000 :
0,2669 × 60 × 3600 = 1k,162.
Hätte nun aber die Luft statt 60° dann 90°, so würde dieses Gewicht
nur noch 67000 : 0,2669
× 90 × 3600 = 0k,775
betragen, also nur 0,6 des richtigen, wodurch, wie leicht ersichtlich, die
regelmäßige Verbreitung der Wärme sehr erschwert werden muß.
In Beziehung auf Anlagekosten wird die Luftheizung unter allen Umständen die
wohlfeilste sein; aber sie kann nur bei Neubauten Anwendung finden, bei denen die
Luftzuführungscanäle im Voraus in den Wänden ausgespart werden können.
Auch in Beziehung auf Oekonomie der Heizung wird sie das höchste bieten, insofern
ihre Construction rationell ausgeführt ist. Nach unserer ersten Berechnung bei
104° Evacuationstemperatur würde sie 72837 : 67000 = 100 : x und x = 91,98 Proc.
Nutzeffect geben, aber nur 90108 : 67000 = 100 : x und
x = 74,35 Proc., wenn die Construction so ist, daß
man eine hohe Evacuationstemperatur braucht.
Nehmen wir aber zur Vergleichung verschiedener Heizsysteme nur immer die
vortheilhafteste Construction in Betracht, so würde der Luftheizung der Vorrang ganz
unbestreitbar gebühren, wenn nicht, wie wir schon angedeutet, sie mit dem Nachtheile
behaftet wäre, daß die Bewohner selbst und oft sehr willkürlich den Zufluß der
warmen Luft reguliren, wodurch dann jede Regelmäßigkeit verloren geht; daher eignet
sich dieses Heizsystem vorzüglich nur für große Säle, bei welchen dann die
Luftvertheilung äußerst einfach wird.
Endlich haben wir noch die Dampfheizung als 4. Centralheizsystem anzuführen. Ihre
Kostspieligkeit in der Anlage und die Complicirtheit der Apparate schließen ihren
Gebrauch bei bürgerlichen Wohnungen fast vollständig aus, und ihre Anwendung
beschränkt sich auf Fabrikgebäude, in denen man den Abdampf der Dampfmotoren
benützt, oder dann auf außerordentlich große öffentliche Gebäude, wie Spitäler,
Lehranstalten, Gefängnisse etc.
Sehr häufig wird die Dampfheizung in den letztern Fällen mit Niederdruckwasserheizung
verbunden, und der Dampf nur benützt, um dem Wasser die gewünschte Temperatur zu
geben. Eine solche Combination gestattet in Beziehung auf Regelmäßigkeit der
Beheizung die größte Vollkommenheit und ist daher für Spitäler besonders
empfehlenswerth; für Privatwohnungen wird aber die Hochdruckwasserheizung den Vorzug
verdienen, sobald man sie in einem Maßstab ausführt, der sie ökonomisch macht.
Ein Miethhaus, welches 12 große Wohnungen mit je 5 heizbaren Zimmern enthält, wird
zur Beheizung derselben in einem mäßig kalten Klima eine Minimalleistung von
360000c pro Stunde erfordern. Würden
nun diese 60 Oefen von den Miethern selbst mit Torf beheizt, so würde der Gesammtaufwand pro
Jahr sehr nahe, à 900 Heizstunden, 371720 Stücke
Torf zu 0k,5 sein, welche 5,6 M. pro
Tausend circa 2090 M. kosten, also pro Wohnung 174 M. nebst einem nicht
unbedeutenden Arbeitsaufwande für das Zutragen des Brennstoffes, Besorgung der Oefen
und mit der Unannehmlichkeit von viel Staub und Unordnung aller Art. Es wird daher
die Mehrzahl der Miether mit Vergnügen jährlich 160 M. mehr Miethe bezahlen, wenn
dafür ihre Wohnung regelmäßig und hinreichend beheizt wird.
Es stellt sich nun die Frage, wie würde der Vermiether dabei seine Rechnung
finden?
Vor Allem würde er bei einer centralen Hochdruckheizung dem Torfe Steinkohle
substituiren können. Davon würde er für 900 Heizstunden und 91 Proc. Nutzeffect
brauchen: 360000 × 900 : 0,91 × 7509 = 47416k, welche zu 24 M. pro 1000k = 1138 M. kosten. Wir wollen annehmen,
daß er seinem Portier für die Besorgung der Heizung jährlich eine Entschädigung von
160 M. gebe, so sind seine Auslagen nahezu 1360 M., was pro Wohnung (1300 : 12) ca.
108,5 M. ausmacht, und er würde also pro Wohnung einen Gewinn von 160 – 108,5
= 51,5 M. oder im Ganzen 618 M. erzielen.
Eine solche Centralheizung würde bei rationeller Construction nicht mehr als ca.
1300m Röhren und daher 3466 M. kosten,
was zu 8 Proc. einen Jahreszins von 277,3 M. ausmacht. Das würde freilich den vorher
berechneten Gewinn von 618 M. wieder auf 340,7 M. herunter bringen, aber immer noch
vortheilhaft sein, da sich das ausgelegte Kapital mit beinahe 18 Proc. verzinst.
Noch vortheilhafter stellt sich die Sache dar, wenn das Haus erst zu bauen ist,
wodurch dann 60 × 80 = 4800 M. für die Oefen erspart werden. Der Zins dieser
zu 8 Proc. 384 M. fügt sich dann dem Gewinn von 340,1 M. hinzu und das jährliche
Benefice wird ca. 720 M., was doch gewiß aller Beachtung werth ist.
Würde es sich um Arbeiterwohnungen handeln, in welchem Falle der Gewinn diesen
zukommen sollte, so würde der Arbeiter für jedes innehabende beheizte Zimmer immer
statt 2090 : 60 = 34,8 M. nur noch 1360 : 60 = 22,7 M. auszugeben haben.
Man kann annehmen, daß 1000 Einwohner im Durchschnitt für das Bedürfniß der Heizung
jährlich das Aequivalent von 700k
Steinkohlen brauchen. Wenn nun auch blos 1/3 dieses Bedürfnisses durch solche
Centralheizungen von 700 auf 450 reducirt würden, so würde das doch für einen Staat,
der 30 Millionen Einwohner hat, eine Ersparniß von 2500 Tausend Kilogramm
Steinkohlen geben, welche einen Geldwerth von 60000 M. repräsentiren. Dies ist freilich
nur ein Tropfen im Vergleiche mit dem totalen Brennstoffconsum, aber wer nicht da
spart, wo es möglich ist, der kommt zu Nichts.
Tafeln