| Titel: | L. Vojacek's gedrehte Radzähne. |
| Fundstelle: | Band 228, Jahrgang 1878, S. 105 |
| Download: | XML |
L. Vojacek's gedrehte Radzähne.
Mit einer Abbildung auf Tafel 6.
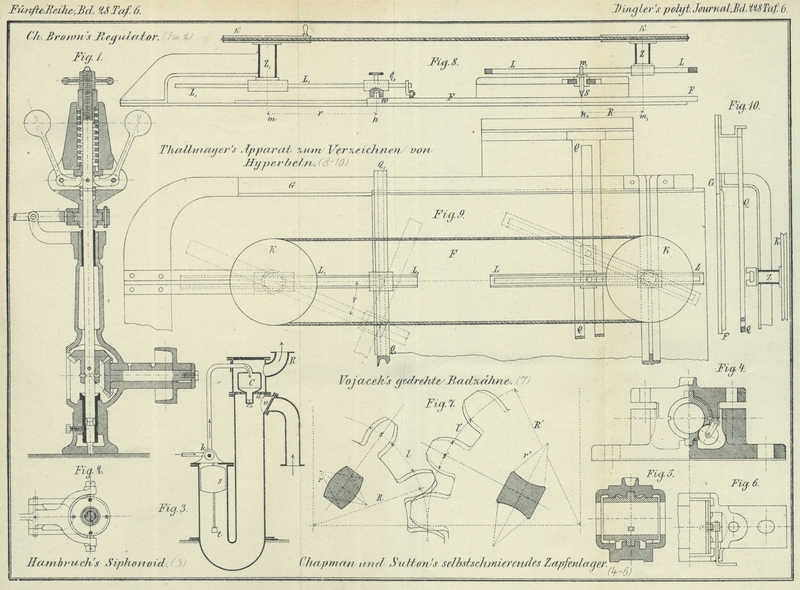
Vojacek's gedrehte Radzähne.
Das übliche Universalgelenk hat bekanntlich den in vielen Fällen schädlichen
Nachtheil, daſs die Winkelgeschwindigkeiten der beiden Achsen nicht in jedem Momente
gleich sind, wodurch eine ruckweise Bewegung entsteht. Die Ansicht, daſs sich diesem
Uebel nur durch complicirte Mechanismen abhelfen läſst, ist allgemein verbreitet,
und es mag deshalb von einigem Interesse sein, eine ziemlich einfache Lösung kennen
zu lernen, welche L. Vojacek (Die
Eisenbahn, 1877 S. 138) bereits vor mehreren Jahren
angegeben und ausgeführt hat.
Die Zahnflanken zweier in einander greifender Stirnräder sind bei der üblichen
Einrichtung durch Cylinderflächen gebildet, deren Grundlinie eine Cycloïde oder eine
Evolvente zu sein pflegt. Bei der in Fig. 7 Taf. 6 abgebildeten
Construction sind diese Flanken aus Rotationsflächen gebildet, deren Erzeugende zwar
dieselbe Cycloïde oder Evolvente sein kann, die sich aber dann je um eine Achse
drehen muſs, um die Flankenflächen zu erzeugen. Diese Drehachse liegt bei dem einen
Rade in der Mitte zwischen zwei Zähnen, während sie bei dem zweiten Rade in der
Zahnmitte gelegen ist.
Der mathematische Berührungsort bei gewöhnlichen Zähnen zweier in
einander greifender Stirnräder ist eine gerade Linie, welche parallel zu den Achsen
liegt. Hier kann man sich statt dieser Berührungslinie zwei Kreisbogen denken, von
welchen der an dem hohlen Zahne gedachte nur ein wenig gröſser ist als derjenige,
welcher dem ausgebauchten Zahne angehört. Um sich davon zu überzeugen, nehme man die
Radhalbmesser, die mittleren Zahndicken und die Theilungen beider Räder gleich groſs
an. Dann ist, wenn s die Zahndicke und l die Zahnlücke bezeichnet, bekanntlich
l=s\left(1+\frac{1}{n}\right), wo n eine Zahl bedeutet, welche zwischen 10 und 50 angenommen wird. Nun ist
nach dem oben Gesagten nahezu:
r=s+\frac{l}{2}=\frac{s}{2}\left(3+\frac{1}{n}\right),\
r_1=l+\frac{s}{2}=\frac{s}{2}\left(3+\frac{2}{n}\right), also
\frac{s}{2}\,\frac{1}{n}=(r_1-r),
so daſs der Halbmesser der hohlen Fläche um 1/40 bis 1/200 der Theilung
gröſser ausfällt als derjenige der ausgebauchten Fläche, was einen schönen Anschluß
der entsprechenden Zähne hervorbringt.
Wenn nun die zu einander parallelen Achsen der beiden Stirnräder
derart gegen einander geneigt werden, daſs sie dabei die gemeinschaftliche Ebene
nicht verlassen, so ist ohne weiteres ersichtlich, daſs die Regelmäſsigkeit des
Eingriffes nicht beträchtlich geändert wird. Dies ist auch bis zu einer gewissen
Grenze der Fall, wenn die geneigten Achsen nicht mehr in derselben Ebene liegen, und
der gute Eingriff wird erfahrungsgemäſs auch dann nicht gestört, wenn sich die
Achsen ein wenig in ihrer Länge verschieben.
In der Figur ist, des leichtern Verständnisses wegen,
s=s' und l=l' angenommen worden. Dabei
würden die hohlen Zähne zu dick ausfallen, und man wird bei der Ausführung besser
etwa (s-s')=\frac{b^2}{4\,r} annehmen können, wenn nämlich mit
b die Zahnbreite bezeichnet wird.
Die Herstellung dieser Zähne unterliegt keinen besonderen Schwierigkeiten, wenn es
sich um präcisen und dauerhaften Eingriff handelt und wenn man sich dafür eine
geeignete Werkzeugmaschine herrichtet. Man erlangt dabei den Vortheil einer gröſsern
Genauigkeit und auſserdem können etwa abgenutzte Zähne sehr genau durch einfaches
Nachdrehen ausgebessert werden. In Fällen, wo man es nicht mit gegossenen Zähnen zu
thun hat, wird die vorliegende Construction jedenfalls der üblichen vorzuziehen
sein, selbst wenn es sich gar nicht um eine Universalgelenk-artige Verzahnung,
handelt.
Tafeln