| Titel: | Apparat zum Verzeichnen von Hyperbeln. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 228, Jahrgang 1878, S. 106 |
| Download: | XML |
Apparat zum Verzeichnen von
Hyperbeln.
Mit Abbildungen auf Tafel
6.
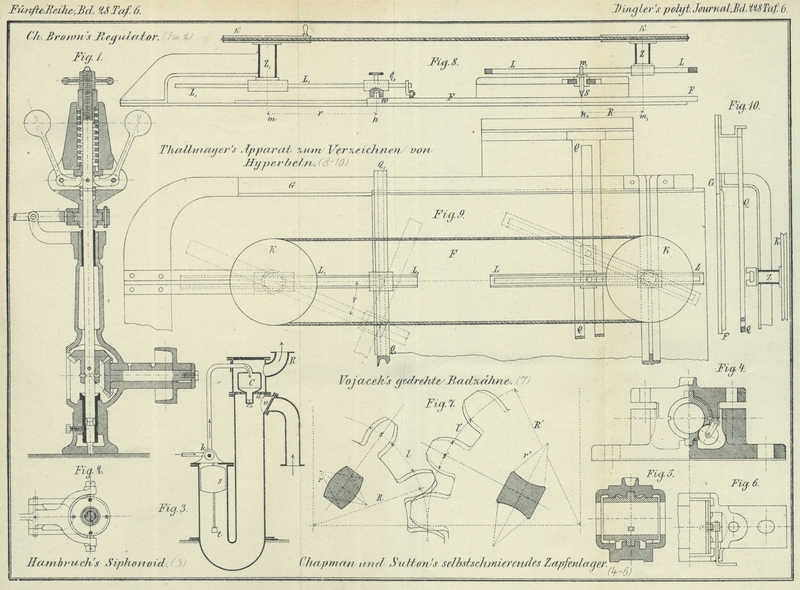
Thallmayer's Apparat zum Verzeichnen von Hyperbeln.
Der in Fig. 8
bis 10 Taf. 6
dargestellte Apparat gestattet die Verzeichnung von Hyperbeln zu gegebenen reellen
und imaginären Halbachsen. Der Beschreibung des Apparates sei jedoch folgende
Bemerkung vorausgeschickt.
Ist x^2R^2+y^2r^2=r^2R^2 die Gleichung einer
Ellipse, und setzt man darin x=z\,cos\,\varphi, so wird
y=R\,sin\,\varphi. Setzt man in der Gleichung
2\,Ry^2=r^2x einer Parabel, die auf der Sehne
2\,r aufsteht und eine Pfeilhöhe 2\,R hat,
x=2\,R\,cos^2\varphi, so wird
y=r\,cos\,\varphi, wobei sich der Werth von x auch noch x=R+R\,cos^2\varphi
schreiben läſst. Durch diese Substitutionen bekommt man also für die Ellipse
x=r\,cos\,\varphi,\ y=R\,sin\,\varphi und für die Parabel
x=R+R\,cos^2\varphi,\ y=r\,cos\,\varphi. Läſst man daher
einen Stift gleichzeitig nach zwei auf einander senkrechten Richtungen dem in den
Gleichungen für x und y
ausgedrückten Gesetze nach sich bewegen, und zwar in der einen Richtung nach dem
durch x gegebenen und in der andern nach dem durch y gegebenen Gesetze, so beschreibt er eine Ellipse
bezieh. eine Parabel. Dasselbe geschieht auch dann, wenn der Stift nur nach einer
Richtung nach einem dieser Gesetze bewegt, und die Fläche, auf welcher er zeichnet,
nach dem andern Gesetze in Bewegung versetzt wird, und zwar in einer auf die
Bewegungsrichtung des Stiftes senkrechten Richtung. Von diesen Gesichtspunkten wurde
bei dem Entwürfe der früher (* 1878 227 337. 430. 592)
beschriebenen Ellipsographen und Parabolographen ausgegangen.
Wendet man den oben befolgten Vorgang auf die Gleichung
x^2R^2-y^2r^2=r^2R^2 einer Hyperbel an, indem man
y=R\,tg\,\varphi setzt, so wird
x=r\,sec\,\varphi. Ertheilt man daher einem Stifte die
Bewegung nach dem Gesetze R\,tg\,\varphi und einer unter ihm
befindlichen Fläche in einer auf die Bewegungsrichtung des Stiftes senkrechten
Richtung die Bewegung nach dem Gesetze r\,sec\,\varphi, so muſs
der Stift auf ihr eine Hyperbel verzeichnen, deren reelle Halbachse rund deren
imaginäre Halbachse R ist.
Bei dem vorliegenden Apparate sind zwei auf einander senkrechte Bewegungen in diesem
Sinne eingeleitet. In den Figuren sind mit Z und Z1 zwei verticale
Zapfen bezeichnet, die sich mit gleicher Winkelgeschwindigkeit drehen und in welche
Lineale L und L1 eingeschoben sind. Auf dem Lineal L1 befindet sich ein
Querlineal Q1, welches
mit einer an seiner Unterseite befindlichen Nuth eine in die Unterlagsfläche F eingesetzte Warze w
umgreift. Die die Unterlagsfläche F bildende Tafel wird
von zwei Führungschienen G aufgenommen. Dreht sich nun der Zapfen Z1 um seine Achse, so
wird die Gleitfläche F nach dem Gesetze rsecφ bewegt, wobei mit r
die Entfernung mn vom Zapfenmittel m bis zum Warzenmittel n
bezeichnet ist.
Vor dem Zapfen Z befindet sich ein geschlitztes
Querlineal Q, dessen Seitentheile die Führungsbacken
für das den Stift S aufnehmende Führungsstück bilden.
Ueber dem obern Theile des Stiftes befindet sich eine Warze w1, welche die zwei Kanten des Schlitzes
im Lineale L umgreifen. Dreht sich nun der Zapfen Z um seine Achse, so wird der Stift S längs der Kante des Lineals Q nach dem Gesetze Rtgφ verschoben, wobei mit
R die Entfernung m1
n1 vom Zapfenmittel m1 bis zum Warzenmittel
n1 bezeichnet ist.
Werden nun die zwei Zapfen Z und Z1 durch eine Schnur
oder durch zwei mit einer Schiene verbundene Kurbeln oder durch Kegelräder mit
gleicher Winkelgeschwindigkeit zu gleicher Zeit in Bewegung gesetzt, so beschreibt
der Stift auf der Fläche F eine Hyperbel, deren
imaginäre Halbachse R und deren reelle Halbachse r ist.
Das Querlineal Q muſs, um auf verschiedene Entfernungen
von dem Zapfen Z eingestellt werden zu können, zum
Verschieben eingerichtet sein, was in den Abbildungen angedeutet ist. Die Lineale
L und Ll können leicht zum Verschieben und Feststellen in
den Zapfen Z und Z1 eingerichtet werden. Das Uebergewicht des an L1 befindlichen
Querlineals Q1 kann
durch eine am Ende desselben angebrachte Laufrolle ausgeglichen werden.
Will man den Apparat zum Verzeichnen von Hyperbeln auf feststehender Unterlagsfläche
geeignet machen, so müſste das Querlineal Q1, anstatt die Unterlagsfläche F, den Zapfen Z und das
Querlineal Q zu fortschreitender Bewegung veranlassen
und gleichzeitig müſste sich auch der Zapfen Z um seine
Achse drehen. Diesen Anforderungen kann mit Anwendung zweier Paare Kegelräder (von
denen das den Zapfen Z betreibende auf seiner Welle
sich verschieben kann) zur Uebertragung der Bewegung vom Zapfen Z auf den Zapfen Z1 in ganz ähnlicher Weise entsprochen werden, wie
bei den früher beschriebenen Ellipsographen.
Die oben angenommenen Gleichungen
x=r\,cos\,\varphi, y=r\,sin\,\varphi,
ferner x=2\,R\,cos^2\varphi, y=r\,cos\,\varphi
und x=r\,sec\,\varphi, y=R\,tg\,\varphi sind
unabhängig von dem Winkel, welchen die zwei Bewegungsrichtungen mit einander
einschlieſsen; es wird daher die resultirende Bewegung auch dann noch nach einem
Kegelschnitte erfolgen, wenn die zwei Seitenbewegungen im Sinne obiger Gleichungen
unter einem beliebigen Winkel vor sich gehen. Der Unterschied gegenüber dem Falle,
wo die zwei Bewegungsrichtungen einen rechten Winkel einschlieſsen, besteht darin,
daſs an die Stelle der gewöhnlichen Halbmesser conjugirte treten. Die Gleichungen
der Parabel enthalten in der oben angenommenen Form die nur innerhalb der
Grenzwerthe ± 1 sich bewegende Gröſse cos φ, was dem
ersten Anscheine nach, da die Parabel keine geschlossene Curve ist, befremdend
erscheinen könnte; es findet aber die resultirende Bewegung eines freien Punktes
immer in einer Parabel statt, wenn die auf ihn einwirkenden Seitenbewegungen
Gleichungen von der Form y=A\,(\varphi t) und
x=B\,(\varphi t)^2 entsprechen, wobei A und B constante Gröſsen bedeuten und (φt) eine beliebige Function einer veränderlichen Gröſse t sein kann, – gerade so wie stets die geradlinige
Bewegung eines freien Punktes resultirt, wenn die auf ihn einwirkenden
Seitenbewegungen nach Gleichungen von der Form x=A\,(\varphi t),
y=B\,(\varphi t) vor sich gehen, und wie z.B. die
resultirende Bewegung in einer Hyperbel geschehen muſs, wenn die Seitenbewegungen
Gleichungen von der Form x=A\,(\varphi t) und
y=B\,\frac{1}{\varphi t} zu Grunde liegen. Die Anzahl der
Seitenbewegungen kann hierbei eine ganz beliebige sein; bei Annahme von blos zwei
Seitenbewegungen erhält man durch Elimination von (φt)
im ersten Falle die Gleichung By^2=A^2x (Parabel), im zweiten die
Gleichung Ay=Bx (Gerade) und im dritten die Gleichung
xy=AB (Hyperbel). Im zweiten Falle stimmt das Wesen oder die
Natur der resultirenden Bewegung mit jenem der Seitenbewegungen überein, indem die
Länge ρ, der nach Verlauf einer gewissen Zeit vom
Punkte zurückgelegten Wegstrecke, wenn Δ den Winkel
bezeichnet, unter welchem die zwei Seitenbewegungen vor sich gehen, sich durch die
Formel \varrho=(\varphi t)\sqrt{A^2+B^2+2\,AB\,cos\,\Delta}
ergibt, welche Formel auſser den Constanten, auch (φt),
die Eigentümlichkeit der zwei Seitenbewegungen enthält.
V.
Thallmayer.
Tafeln