| Titel: | Ueber Leistung des Luftstrahlgebläses bei Anwendung verschiedener Düsen und verschiedener Formen des den Strahl und die mitgerissene Luft aufnehmenden Ansatzrohres. |
| Autor: | L. P. |
| Fundstelle: | Band 228, Jahrgang 1878, S. 293 |
| Download: | XML |
Ueber Leistung des Luftstrahlgebläses bei
Anwendung verschiedener Düsen und verschiedener Formen des den Strahl und die
mitgerissene Luft aufnehmenden Ansatzrohres.
Mit Abbildungen auf Tafel
20.
De Romilly's Versuche über die Leistung des
Luftstrahlgebläses.
Im Bulletin de la Société
d'Encouragement, 1877 Bd. 4 S. 409 berichtet Haton de la Goupillière über die oben genannten
Versuche, welche Felix de Romilly in umfassender Weise
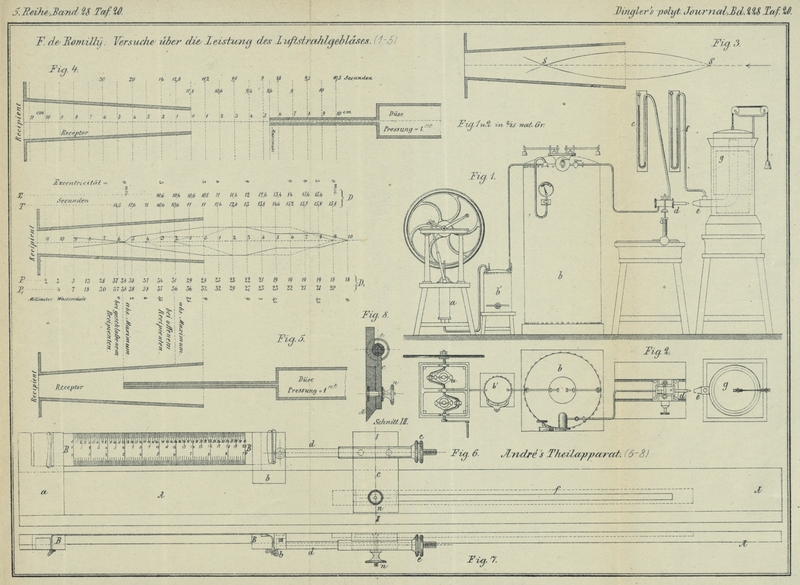
mit dem in Fig.
1 und 2 Taf. 20 dargestellten Apparat durchgeführt hat. Derselbe besteht aus
einer zweicylindrigen Luftpumpe a, durch welche ein
Luftkessel b mit comprimirter Luft gefüllt wird; der
die Pumpe bedienende Arbeiter ist im Stande, durch Beobachtung eines mit der Düse
d in Verbindung stehenden Quecksilbermanometers c den Gang der Luftpumpe so zu leiten, daſs die
Pressung der Luft im Kessel b und namentlich vor der
Düse d constant bleibt. Auſserdem ist der Kessel b noch mit einem Federmanometer versehen und zwischen
die Luftpumpe und den Kessel b ein Ausgleichbehälter
b' eingeschaltet, um den Einfluſs der Stöſse der
Pumpenkolben auf die Spannung in b aufzuheben.
Der aus der Düse d strömende Luftstrahl tritt
vollständig in ein mehr oder weniger entfernt von der Düsenmündung befindliches Rohr
e ein, indem er hierbei eine von den jeweiligen
Verhältnissen abhängige Luftmenge mit sich fortreiſst, welche gleichzeitig in das
Ansatzrohr eindringt. Mittels einer mit diesem Ansatzrohre e in Verbindung stehenden, auf Wasser schwimmenden Gasometerglocke g kann einerseits das Volum der in der Zeiteinheit in das Ansatzrohr e eintretenden gesammten Luftmenge gemessen werden; andererseits läſst
sich, wenn das hintere Ende des Ansatzrohres e dicht
verschlossen wird, die durch das Luftstrahlgebläse in dem Rohre erzielte Pressung
mittels eines Wassermanometers f bestimmen. Durch
entsprechend angeordnete Stellschrauben kann das Düsenmundstück in Bezug auf die
Mündung des Ansatzrohres e in alle für die Anstellung
der fraglichen Versuche erforderlichen Lagen gebracht werden.
Auf die durch den Luftstrahl mitgerissene und in das
Ansatzrohr e (den Receptor) hineinbeförderte Luftmenge hat die Form der
Mündung des Receptors einen hervorragenden Einfluſs, und zwar ist diese
Luftmenge am kleinsten bei Anwendung einer Oeffnung in dünner Wand und am gröſsten
bei Anwendung eines conischen Ansatzrohres, dessen kleinerer Querschnitt der Düse
zugekehrt ist. Nachstehend das Verhältniſs der Bewegungsgröſsen der injicirten Luft bei Anwendung verschiedener Formen
des Receptors:
Conisches Ansatzrohr von 5 bis 7° Divergenzwinkel (divergent im Sinne der Bewegung)
100
Conisches Ansatzrohr von 15° Divergenzwinkel (divergent im Sinne der Bewegung)
81
Conisches Ansatzrohr von 5 bis 7° Convergenzwinkel (convergent im Sinne der Bewegung)
65
Cylindrisches Ansatzrohr
61
Oeffnung in dünner Wand
48.
Auf die Menge der in der Zeiteinheit injicirten Luft üben ferner noch folgende
Umstände einen sehr merkbaren Einfluſs aus:
1) Der Winkel zwischen der Achse der Düse und derjenigen des Receptors; die
günstigsten Resultate ergaben sich dann, wenn dieser Winkel gleich 0 war, d.h. wenn
beide Achsen in eine gerade Linie fielen oder wenigstens parallel liefen.
2) Die Entfernung der Düsenmündung von der Mündung des Receptors; z.B. ergab sich für
1at Ueberdruck im Düsenbehälter das Maximum
der injicirten Luftmenge, wenn die Entfernung der Düsenmündung von derjenigen des
Receptors nahezu gleich dem 4fachen Durchmesser der letzteren war.
3) Die Gröſse der Mündung des Receptors, und zwar lieſsen die Versuche erkennen, daſs
die injicirte Luftmenge proportional dem Durchmesser
(nicht dem Querschnitt) dieser Mündung wuchs. Diese Erscheinung erklärt sich daraus,
daſs offenbar die Menge der durch den Luftstrahl mitgerissenen Luft abhängig ist von
dem Umfange des Strahles, und daſs die Geschwindigkeit
der mitgerissenen Lufttheilchen am gröſsten ist in unmittelbarer Nähe obigen
Umfanges und allmälig abnimmt, je weiter das Lufttheilchen von demselben entfernt
ist.
4) Die Stellung der beiden, als parallel vorausgesetzten Achsen der Düse und des
Receptors: a) bei Anwendung eines conischen Ansatzrohres von ungefähr 6°
Divergenzwinkel und in einer zur Bewegungsrichtung divergenten Stellung ergab sich sowohl für die injicirte Luftmenge, als
auch für die hervorgerufene Pressung bei geschlossenem
Recipienten stets ein Maximum, wenn beide Achsen in eine gerade Linie fielen; b)
befand sich dagegen das Ansatzrohr in einer zur Bewegungsrichtung convergenten Stellung, so erhielt man sowohl in Bezug
auf injicirte Luftmenge, als in Bezug auf hervorgerufene Pressung bei gewissen Lagen
der Düsenmündung gegen das Ansatzrohr relative Maxima,
wenn die Düsenachse mehr oder weniger von der Achse des Ansatzrohres entfernt
wurde.
Fig. 3 Taf. 20
gibt ein Bild letzterer Verhältnisse; die Curven SS'
bilden die Meridianlinien einer Rotationsfläche, deren Oberfläche den geometrischen
Ort der verschiedenen Stellungen der Düsenachse bei dem Erscheinen der oben
genannten relativen Maxima bildet; das absolute Maximum
erschien stets, wenn die Düsenachse mit der Achse des Ansatzrohres zusammenfiel,
z.B. in Fig. 3
im Punkte S.
Zum Schlüsse möge die Angabe einiger Versuche de Romilly's folgen.
1) Den günstigsten Effect gibt ein conischer Receptor von 5 bis 7°
Divergenzwinkel in der Stellung Fig. 4 Taf. 20. Bei einem
Durchmesser der vorderen (kleineren) Oeffnung von 16mm und einer Lange von 114mm, einer Düse
bestellend aus einem feinen Rohre von 1mm,5
Durchmesser und 92mm Länge wurde die Füllung des
Recipienten bei verschiedenen Entfernungen des Düsenmundstückes von der Mündung des
Receptors in den beigeschriebenen, in Secunden angegebenen Zeiträumen erzielt. Das
Maximum des Effectes, entsprechend dem Minimum der Füllungszeit (8,6 Secunden), trat
ein bei einem Abstande des Düsenmundstückes vom Receptor von ungefähr 54mm. Das Maximum der Pressung (bei geschlossenem
Recipienten) betrug 51mm Wassersäule; hierbei
hatte die Düse von obigem Durchmesser eine Länge von 170mm.
2) Für einen conischen Receptor von 7° Convergenzwinkel in der
Stellung Fig.
5 Taf. 20 erscheint das absolute Maximum,
sowohl bezüglich der injicirten Luftmenge, als der hervorgerufenen Pressung, wenn
sich das Düsenmundstück innerhalb des Receptors und
zwar in der Achse desselben befindet 5 die relativen
Maxima dagegen treten bei andern Lagen des Düsenmundstückes ein, sobald die
Achse desselben in gewissen Entfernungen von der Achse des Receptors zu letzterer
parallel gerichtet ist. In Fig. 5 geben die punktirten Linien die Stellungen der Düse D von 1mm,5
Durchmesser und 92mm Länge für die relativen
Maxima bei offenem Recipienten, die Zahlen hinter T die Füllungszeiten desselben, wenn die Düse in der
Achse des Receptors, die Zahlen hinter T die
Füllungszeiten bei excentrischer Düsenstellung an, während die obersten vertical
stehenden Zahlen die Gröſse dieser Excentricität bezeichnen. Die Stellung der Düse
bei dem absoluten Maximum ist, wie aus der Figur
ersichtlich, nicht ganz scharf ausgeprägt. Die ausgezogenen Linien geben die Stellungen der Düse D1 von 1mm,5 Durchmesser und 170mm Länge für die
relativen Maxima bei geschlossenem Recipienten, die Zahlen hinter P die erhaltenen Pressungen innerhalb desselben bei centrischer Stellung
der Düse, die Zahlen hinter P1 die Pressungen bei excentrischer Stellung derselben und die untersten
verticalen Zahlen die Gröſse der Excentricität an 5 hier findet sich die Stellung
der Düse bei dem absoluten Maximum schärfer
ausgeprägt.
3) Wird die Düse durch eine Oeffnung von 1mm Durchmesser in dünner Wand gebildet, wobei in
Folge der Contraction der ausströmende Luftstrahl nur 0mm,8 Durchmesser besitzt, so ergeben sich für einen Ueberdruck in der
Düsenkammer von 1at folgende Verhältnisse:
Durchmesser des Receptor
mm
dichtange-schlosseneDüse
4
8
16
32
Füllungszeit des Gaso- meters von
48l Inhalt
Sec.
173
34
17
8,5
4,2
Secundlich
injicirte Luftmenge
l
0,282
1,41
2,82
5,64
11,42
Mittlere Geschwindigkeit der
eintretenden Luft
m
564
112,09
56,40
28,20
14,25
Bezeichnet D den Durchmesser der
Oeffnung des Receptors, d den Durchmesser der Düse, so
ist im Allgemeinen die injicirte Luftmenge proportional dem Werthe
\frac{D}{d}, die mittlere Geschwindigkeit der in den Receptor
eintretenden Luft dagegen proportional dem Werthe \frac{d}{D} und
die bei geschlossenem Recipienten erzielte Luftpressung umgekehrt proportional dem
Werthe D2. –
Referent findet es hier am Platze, an die im Organ für die Fortschritte des Eisenbahnwesens, 1865 S.
97 bis 138 veröffentlichten, sehr umfangreichen Versuche von Obermaschinenmeister
Prüsmann, betreffend die „Ermittelung der
Wirkung des Locomotivblasrohres und die Auffindung einer rationellen Form für
die Locomotivschornsteine“ zu erinnern, welche u.a. zu dem Resultate
führten, daſs durch Anwendung eines von unten nach oben conoidisch erweiterten
Schornsteines, dessen engster Querschnitt in richtiger Entfernung von der
Blasrohrmünduung fixirt wurde, eine erheblich gröſsere Luftverdünnung innerhalb der Rauchkammer
erzielt wird, als durch die früher allgemein und auch jetzt noch vielfach
angewendeten cylindrischen Schornsteinröhren. Obwohl hier das Dampfstrahlgebläse zur
Verwendung gelangt. so bieten doch die Resultate dieser Versuche mit den oben
angeführten bemerkenswerthe Analogien.
L.
P.
Tafeln