| Titel: | Tasimeter von F. A. Schöpfleuthner, Maschinen-Ingenieur in Wien. |
| Autor: | F. A. Schöpfleuthner |
| Fundstelle: | Band 234, Jahrgang 1879, S. 356 |
| Download: | XML |
Tasimeter von F. A. Schöpfleuthner,
Maschinen-Ingenieur in Wien.
Mit Abbildungen auf Tafel 28.
Schöpfleuthner's Tasimeter.
Betrachtet man eine in Bewegung begriffene Dampfmaschine und verfolgt den Gang des
Kreuzkopfes, der Pleuelstange oder der Kurbel, wobei die Massenträgheit nicht
unberücksichtigt zu lassen ist, so erstaunt man geradezu über die anscheinend
gleichgiltige Ruhe, mit welcher dieser stählerne „Organismus“ so
auſserordentliche Arbeitsleistungen entwickelt; denn man sieht, wie die in linearer
Richtung arbeitenden Theile, deren Glieder abwechselnd zwischen Ruhe und Bewegung
schwanken, dem im Kreise sich drehenden Kurbelzapfen so zu sagen willenlos und ohne
Widerstand folgen.
Das am Indicator beobachtete Diagramm zeigt eine Curve, deren Gesetz mit jenem der
oben angezogenen Bewegungsart gar nichts gemein hat und deren Ordinaten zwar
gleichfalls zwischen Null und einem Maximum liegen; allein diese Maxima bezieh.
Minima fallen nicht in denselben Zeitabschnitt und es muſs daher diese Toleranz
durch Auftreten sehr bedeutender Materialspannungen, d. i. durch Ansammlung von
mechanischer Arbeit in der Gesammtmasse, ausgeglichen werden, sollten dieselben im
geeigneten Augenblick rechtzeitig zur wirksamen Aeuſserung gelangen. Nachdem sich aber diese
unsichtbaren Kräfte weder frei beobachten, noch am abgenommenen Dampfdiagramm
wahrnehmen lassen, so kann es kaum weniger interessant sein, die inneren Vorgänge
der Glieder zwischen Kolben und Schwungrad, d. i. zwischen Ausgangs- und Abgabsort
der mechanischen Arbeit, kennen zu lernen, somit die Verschiedenartigkeit der in
gewissen Zeitabschnitten auftretenden Materialspannungen auf die einfachste und
bequemste Art genau nach Gröſse, Richtung und Dauer zu verfolgen.
Derjenige Ort nun, an welchem die Gesammtsumme aller im Dampfkolben auftretenden
Kräfte zur noch meſsbaren Aeuſserung gelangt, ist die Kurbelachse oder
Schwungradwelle, und es zeigt sich hierin, wie sehr verschieden die in dieser Welle,
also zwischen Schwungrad und Kurbel, auftretende Beanspruchung des Materials
derselben an deren Oberfläche ist, während der Kurbelzapfen einen Bogen von 180°
durchläuft. In Folge der zur Zeit der gröſsten Geschwindigkeit des normalen
Kolbenganges, bezieh. des Durchganges der Kurbel am todten Punkte, in der Welle
auftretenden Torsionskräfte erleidet eine in der Entfernung des Wellenradius
befindliche Faserschicht eine Streckung, deren Dauer von der Anzahl Umgänge der
Welle – in irgend einem Zeitmaſs vollführt – abhängt, deren Gröſse aber von der
hindurch geleiteten mechanischen Arbeit und der Beschaffenheit des Materials bedingt
ist. Diese Spannungen nehmen gegen die geometrische Achse der Welle zu zwar immer
mehr und mehr ab, bis sie endlich ganz aufhören, also Null werden, von hier
ausgehend aber wieder an Gröſse zunehmen und zwar im
entgegengesetzten Sinne, bis im Mittelpunkt dieser kreisförmigen
Querschnittsfläche eine der Anfangsspannung gleiche,
jedoch negative Spannung auftritt, so daſs sich beide Spannkräfte gegenseitig das
Gleichgewicht halten. Der Durchmesser dieser in sich zurückkehrenden, ringförmigen
todten Faserschicht – Neutralcylinder – läſst sich
zwar durch einfache Rechnung bestimmen (er ist weit gröſser als der Wellenradius);
allein hier bedarf es vorläufig der Kenntniſs desselben nicht.
Denkt man sich am Umfange der Welle, zwischen Kurbel und
Schwungrad, eine sehr kleine Faserschicht in achsialer Richtung herausgeschnitten
und durch ein gehärtetes Stahlband von entsprechendem Querschnitt ersetzt und gibt
man diesem Stahlbande eine Anfangsspannung = p, so
wird, wenn es durch irgend einen Einfluſs von auſsen in eine schwingende Bewegung
versetzt ist, die Anzahl n der transversalen
Schwingungen in der Secunde zu berechnen sein aus der FormelVgl. Wüllner:
Experimentalphysik, 3. Auflage Bd. 2 S. 483.:
n=\frac{1}{2}\,\sqrt{\frac{gp}{ql}}, .
. . . . . . . . (1)
wenn g = 9,81, q und l das Gewicht
bezieh. die Länge des Bandes bezeichnen.
Nehmen im Augenblicke des Angreifens einer Kraft an der Kurbel die
einzelnen Fasercylinder der Welle eine spiralförmige Lage an, so muſs auch eine
Spannung eintreten, welche in der Ruhelage in den Fasern nicht vorhanden war, da ja die Welle aus obigen
Gründen nicht so viel verkürzt wird, als zur Aufhebung dieser Spannung nöthig wäre.
Weil sich aber diese Spannungsänderungen auch in dem eingelegten Stahlbande und zwar
in gleicher Gröſse kund geben, so muſs die der neuen Spannung entsprechende
Schwingungszahl n1 nach
Gleichung (1) sein:
{n_1}^2=\frac{g(p+\Delta p)}{4\,ql} . .
. . . . . . (2)
und die dadurch entstandene Verlängerung desselben
gleich:
\Delta l=\frac{\Delta p}{Ef}\,l, . . .
. . . . . . . . . . (3)
wenn E den
Elasticitätsmodul und f die Querschnittsfläche des
Bandes bezeichnen.
Nun ist aber die Kenntniſs dieser Verlängerung Δl zur Auffindung der Torsionswirkung von vorn
herein nöthig, und da diese Gröſse aus Gleichung (3) nicht ohne weiters bestimmt
werden kann, müssen die bereits bekannten Schwingungszahlen auf eine Normale bezogen
werden, welche durch Zuhilfenahme einer gewöhnlichen, jedoch passenden Stimmgabel
auch thatsächlich erlangt wird. Macht diese Stimmgabel n2 Schwingungen in der Secunde und nennt man
das Verhältniſs \frac{n}{n_2}=d, bezieh.
\frac{n_1}{n_2}=d_1, dann erhält man aus Gleichung (1):
d=\frac{1}{2}\sqrt{\frac{gp}{ql{n_2}^2}} . . . . . . .
(4)
Dividirt man Gleichung (2) durch n22, so ergibt sich
nach Subtraction der Gleichung (4) der Unterschied dieser Verhältnisse:
{d_1}^2-d^2=\frac{g\Delta
p}{4\,ql{n_2}^2}}; . . . . (5)
daraus ist nach Gleichung (3):
\Delta l=({d_1}^2-{d_2}^2)\,c, . . . .
. . . . (6)
wobei c=\frac{4\,ql^2{n_2}^2}{Efg}
einen Ausdruck bedeutet, welcher eine constante Gröſse hat, die von der räumlichen
Ausdehnung des Bandes abzuleiten ist.
Setzt man die Anfangsschwingungen des Bandes n = n2, d. i. jenen der Stimmgabel gleich, so wird d == 1 und der letzte Ausdruck in Gleichung (6) erhält
die Form c (d12 – 1) somit:
\Delta l=c\,({d_1}^2-1) . . . . . . . .
. (7)
Denkt man sich ferner die Spannung des Bandes, anstatt in obiger
Weise, durch eine bleibende Verdrehung der Welle selbst hervorgebracht, so daſs die
Richtung desselben mit der geometrischen Achse der Welle einen Winkel a einschlieſst, und vervollständigt das so entstandene
Dreieck in der Weise, daſs dessen rechter Winkel dem Bande gegenüber liegt, so ist
die kleine Kathete a dieses Dreieckes – Gröſse der
Abweichung – zu bestimmen aus der Gleichung:
a^2=l^2-b^2, . . . . . . . . . .
(8)
worin l obige und b die dem rechten Winkel anliegende Kathete
bezeichnen.
Verbindet man endlich die beiden Endpunkte der Kathete a durch Verlängerung zweier Radien der Welle, so daſs
ein neues Dreieck entsteht, dessen rechter Winkel mit jenem des vorigen auf
derselben Seite liegt, und nennt den Centriwinkel β,
dann wird:
a=(r+h)\,sin\ \beta, . . . . . . . . .
. (9)
wenn (r + h) die Entfernung des Bandendes vom Wellenmittel
bezeichnet.Hier denkt man sich wie früher das Band nicht um die Welle gelegt, sondern in
schiefer Richtung zu derselben – etwa tangential –
ausgespannt.
Ist die Inanspruchnahme der Welle von der Art, daſs die Winkel α und β ihrer Gröſse nach
sich ändern, etwa kleiner werden, nennt man diesfalls die neuen Winkel α1 und β1, sowie die diesem
Dreiecke entsprechende Hypotenuse und Kathete l1 bezieh. a1 dann ist, nachdem b und (h + r)
constant bleiben:
{a_1}^2={l_1}^2-b^2 . . . . . . . . . .
. (10)
und
a_1=(r+h)\,sin\ \beta_1 . . . . . . . .
. (11)
Subtrahirt man Gl. (11) von (9), so folgt a – a1 = (r + h) (sin β – sin β1), und wenn der letzte Ausdruck der
rechten Seite dieser Gleichung mit sin ῳ
bezeichnet wird:
sin\,\omega=\frac{a-a_1}{(r+h)} . . . .
. . . . (12)
Aus Gleichung (8) und (10) folgt aber l2 = a2 + b2 und l12 = a12 + b2; demnach ist 12 – l12 = a2 – a12.
Substituirt man für den linksseitigen Ausdruck dieser Gleichung
den in Gleichung (7) aufgenommenen Werth und setzt a12 = a2 – dl2, so wird nach
Gleichung (12):
sin\,\omega=\frac{a+dl^2}{r+h}-\frac{a^2}{r+h} . . . . . . .
(13)
Diese Formel dient also zur Bestimmung des
Torsionswinkels ῳ, aber nur dann, wenn die Anzahl der Schwingungen, welche
der Anfangsspannung des Bandes entspricht, jener der Stimmgabel gleich war, d.h.
wenn beide gleiche Tonhöhe hatten.
Der Einfluſs der Temperatur auf das Band während der Versuchsdauer
ist von so geringer Bedeutung, daſs ohne Bedenken davon abgesehen werden kann.
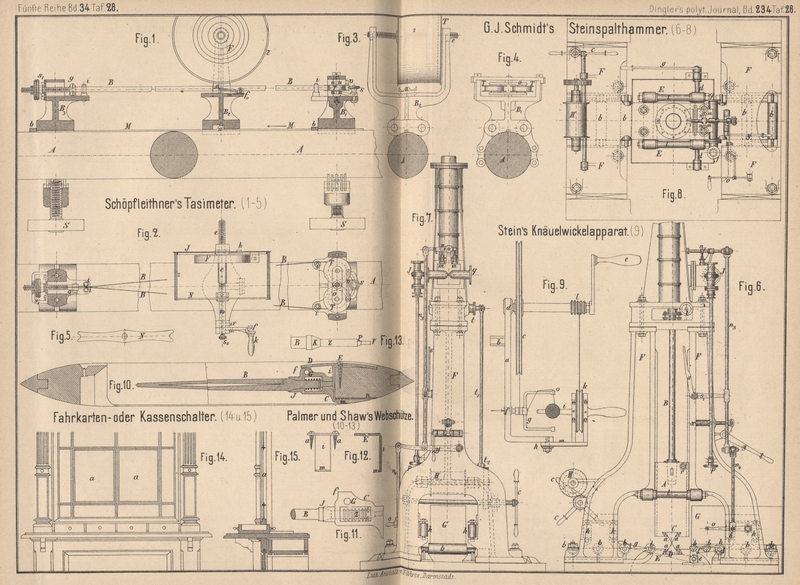
Auf Grund vorliegender Entwicklung, ist das nachstehend beschriebene und auf Taf. 28
in Fig. 1 bis 5 in
angenähert ⅓ n. Gr. abgebildete Instrument construirt.
Auf einer Welle A befinden sich die Backen B1, B2 und B3 mittels
Flügelschrauben s und Kette (Fig. 4)
derartig festgeschraubt, daſs eine Verschiebung unmöglich ist. Die Kette bezweckt,
alle vorkommenden Durchmesser zu umspannen. Der Backen B3 ist mit der Spannschraube s1 versehen, deren
Klemmbacken g zwei zwischen den Schneiden der Stifte
i hindurchgeführte Stahlbänder B festhalten; letztere sind an den Backen B1 so um die Trommeln
T geschlungen, daſs sie durch im Innern derselben
befindliche Spiralen selbstthätig aufgewunden werden; damit die Bänder B gleiche Spannung erhalten, sind die Trommeln T so durch einen Doppelhebel o verbunden, daſs sie, sobald der Binder v
(Fig. 2) aufgelegt und dergestalt ein ferneres Abwickeln unmöglich gemacht
ist, um eine gemeinschaftliche Achse balanciren. Haben die Bänder B die der beigegebenen Stimmgabel entsprechende
Spannung, so zieht man die Schraube s an dem Backen B1 fest an, um jede
weitere Bewegung der Trommeln T hintanzuhalten. Der
Backen B2 ist mit einem
Glascylinder z versehen, welcher durch die Querschiene
N (Fig. 2 und
5) und Schraube s0 an die rückwärts befindliche Scheibe J gepreſst wird und von einer im Innern des Cylinders angebrachten Spirale
F in Umdrehung versetzt werden kann. Das Gewinde
der Welle e (Fig. 2 und
3) bewirkt, daſs sich der aus den Theilen z, J,
N und F gebildete Mechanismus nach 6 maligem
Umgange so weit zurückgeschraubt hat, daſs die Nabe von N am Lager der Welle w (Fig. 2)
festsitzt. Durch Drehen an der Kurbel k nimmt das Ganze
seine frühere Stellung wieder ein. Damit jedoch die Spirale F den Cylinder z in Umdrehung versetzen kann,
ist sie mit dem inneren Ende auf der hohl gehaltenen Welle w so befestigt, daſs sich letztere zwar herausschiebt, doch an einer
Drehung durch die Schraube r (Fig. 2)
gehindert wird. Diese
Schraube muſs beim Rückwärtsdrehen und Anspannen der Feder F offen gehalten werden.
Die Kurbel k ist mit einem Sperrhaken f versehen, der sich an die verticale Rippe des Backens
B2 anlegt und auf
diese Weise das Ablaufen der gespannten Feder F
verhütet, so lange nicht die Schraube r angezogen ist.
Der Schieber h (Fig. 2)
verbindet z bezieh. J mit
e in seiner jetzigen Stellung, läſst aber nach dem
Herausziehen diese los, so daſs also die Rückschraubung von w bezieh. e ohne Drehung von z erfolgen kann, wodurch die Feder F um die vorhin abgelaufene Strecke wieder angezogen
wird. Das Herausnehmen und Einsetzen des Cylinders z
erfolgt, indem man die Schraube s0 lüftet und w
zurückzieht, wodurch zwischen e und w eine Oeffnung entsteht, groſs genug, um den Cylinder
der Länge nach hindurch zu lassen. Ein Anker a (Fig.
1 und 3), welcher
sich zwischen die Bänder B legt, diese also ausspannt
und durch rasches Zurückfallen in Schwingungen versetzt, ist drehbar an B2 befestigt und für
diesen Zweck mit einer Feder f0 versehen. Der Stift, welchen die Nase n (Fig. 1)
unterstützt, hält bei Beginn des Versuches den Anker gespannt.
Zwei sehr zarte Stahlspitzen sind auf den Bändern B so
verschiebbar befestigt, daſs sie den berufsten Glascylinder an der tiefsten Stelle
berühren und während seiner Rückwärtsbewegung wellenartige Linien zeichnen, deren
Form von den Schwingungen der Bänder abhängig ist. Sie laufen zu einander parallel
spiralartig um den Cylinder und haben eine Längenausdehnung von je beiläufig 612mm. Damit diese Wellenlinien vollkommen rein
ausfallen, muſs der Backen B2, ebenso die Stahlspitzen, genau in der Mitte der schwingenden
Bandstücke, d. i. der Theil zwischen den vier Stiften i, liegen. Zur leichteren Aufstellung des Instrumentes benutzt man die
untergelegte Meſsstange M, welche zu beiden Seiten mit
Centimetertheilung versehen ist und deren Schieber b
(Fig. 1) für den gewünschten Abstand eingestellt werden müssen. Je zwei
Spitzen in den Schiebern b bewirken, daſs diese
Meſsstange durch bloses Auflegen auf die Welle parallel zu derselben wird und das
Instrument stets genau in dieselbe Ebene fällt. Die gröſste zulässige Entfernung der
beiden Backen B1 und
B3 ist 500mm, die kleinste noch brauchbare dagegen 240mm; der Abstand beider Schreibstifte bleibt in
jedem Falle derselbe.
Ueber die Art der Anwendung dieses Instrumentes bleibt kaum etwas zu sagen; nur
soviel sei noch bemerkt, daſs das an einer guten Expansionsdampfmaschine damit
erzielte Torsionsdiagramm die Form zweier mit der Vorderseite zusammenstoſsender, um
eine Atmosphäre verminderter Dampfdiagramme hat, von denen das erste der gröſsten,
das zweite der kleinsten Füllung – nahezu – entspricht. Es steigt nämlich in einer
concaven Curve rasch an, geht dann bis etwas über die Mitte der Länge zur Abscisse
parallel und fällt in einer Geraden ab. Der Torsionseffect erreicht also während einer
vollführten Umdrehung der Kurbel zweimal ein Maximum und zweimal die Gröſse Null,
vorausgesetzt, daſs die Masse des Schwungringes nicht zu groſs oder zu klein war, in
welchem Falle dann trotz sonst richtiger Indicatordiagramme kein stetiger Verlauf
des Torsionsdiagrammes erzielt wird, ja bei nicht richtiger Dampfvertheilung sogar
eine negative Gröſse oder mehr als zwei Nullpunkte sich einfinden.
Bei Berechnung des Torsionsdiagrammes hat man zu beachten, daſs die im frühern
gegebene Formel nur für das der gröſseren Schwingungszahl angehörige Band gilt. Nach
Beendigung des Versuches theilt man die Oberfläche des Glascylinders mit dem
beigegebenen Streicher in eine Anzahl Abtheilungen, deren Längsseite der
Cylinderachse parallel läuft, übergieſst ihn dann mit Firniſs und läſst gut
abtrocknen. In diesen Rechtecken zählt man dann zwölf quer durchlaufende
Wellenlinien, von denen je die erste und siebente, die zweite und achte u.s.w.,
endlich die sechste und zwölfte als zusammengehörig zu betrachten sind. Die halbe
Summe je zweier zusammengehörigen Wellenlinien ist gleich der dieser Strecke
zugehörigen Anzahl Gabelschwingungen, während der Ueberschuſs der gröſseren
Schwingungszahl diesem in der Berechnung gegenübersteht, also das Mitschwingen der
Stimmgabel gar nicht nöthig ist.
Meine derzeitige Stellung gestattet mir nicht, umfangreichere Versuche mit dem
beschriebenen Instrumente vorzunehmen. Hoffentlich trägt diese Veröffentlichung dazu
bei, daſs mein Tasimeter von berufenen Kreisen eingehender geprüft und beurtheilt
werde
Tafeln