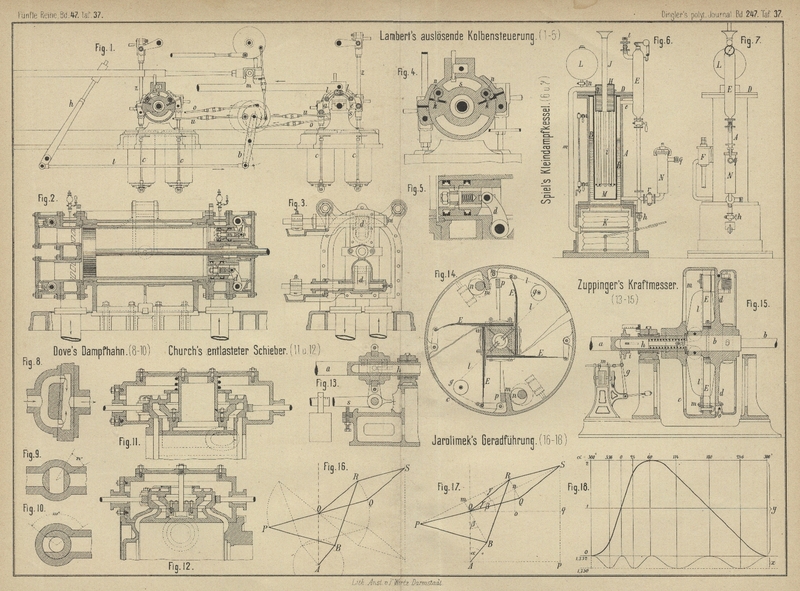
| Titel: | Geradführung mit beschleunigtem Rückgang; von A. Jarolimek. |
| Autor: | A. Jarolimek |
| Fundstelle: | Band 247, Jahrgang 1883, S. 481 |
| Download: | XML |
Geradführung mit beschleunigtem Rückgang; von
A. Jarolimek.
Mit Abbildungen auf Tafel 37.
A. Jarolimek's Geradführung mit beschleunigtem
Rückgang.
Es sei in Fig. 16
Taf. 37 AB=r eine um den Punkt A
rotirende Kurbel.
Wird in dem Abstande OA=2\,r ein um den Punkt O schwingender gleichseitiger Hebel POQ von der Länge PO=OQ=2\,r, sowie
eine zweite ebenfalls um O schwingende Lenkstange von
der gleichen Länge OR=2\,r angebracht und werden einerseits die
beiden Stangen OR und OQ
durch zwei ebenso lange Stangen RS=QS=2\,r zu einem beweglichen
Parallelogramm vereinigt, als wie andererseits die Endpunkte R und P mit dem Kurbelende B durch zwei andere Stangen von der Länge
PB=RB=r\sqrt7 in Gelenken verbunden, so hat diese Anordnung
zur Folge, daſs, wenn die Kurbel AB einmal im Kreise
herumgeht, der Punkt S des Systemes einen nahezu in die Gerade fallenden Hub
hin und zurück und zwar in der Strecke von der Länge 4\,r
vollzieht.
Ist dabei der Gang der Kurbel nach rechts (bezieh. nach dem gerade geführten Theile)
gerichtet, so vollzieht sich der Aufhub des Punktes S
in dem Zeitraum, in welchem die Kurbel aus der Neigung von 60° linkerseits in jene
von 60° rechterseits von der Mittellinie übergeht, also einen Weg von 120°
zurücklegt, so daſs der Niedergang von S die doppelte
Zeit gebraucht.
Bei der Drehung der Kurbel in umgekehrter Richtung erfolgt hingegen der Niedergang
doppelt so schnell als der Aufhub.
Hierbei bestehen folgende Beziehungen: Bezeichnet man die Winkel in Fig. 17
\sphericalangle\,OAB=\alpha,\ \sphericalangle\,AOB=SOq=\beta und
\sphericalangle\,ORm= ROS=\gamma, so ist zunächst im
\triangle\,AOB:\
\overline{BO^2}=\overline{AO^2}+\overline{AB^2}-2\,AO\times AB\ cos\
\alpha und also wegen AO=2\,r und
AB=r:
BO=r\sqrt{5-4\ cos\ \alpha} . . . . . . . .
(1)
Aus AB\ sin\ \alpha=OB\ sin\ \beta und
AB\ cos\ \alpha+OB\ cos\ \beta=OA bestimmt sich dann:
sin\ \beta=\frac{sin\ \alpha}{\sqrt{5-4\ cos\
\alpha}} . . . . . . (2) und cos\ \beta=\frac{2-cos\
\alpha}{\sqrt{5-4\ cos\ \alpha}} . . . . . . (3)
Im Dreieck BmR ist ferner
\overline{BR^2}=\overline{Rm^2}+\overline{Bm^2}, somit wegen
BR=r\sqrt7,\ Rm=OR\ cos\ \gamma=2\,r\ cos\ \gamma und
Bm=BO+Om=r\sqrt{5-4\ cos\ \alpha}+2\,r\ sin\ \gamma
woraus sich bestimmt:
sin\ \gamma=\frac{2\ cos\ \alpha-1}{2\sqrt{5-4\ cos\
\alpha}} . . . . . . . (4)
cos\ \gamma=\sqrt{1-sin^2\gamma}=\frac{\sqrt{19-12\ cos\
\alpha-4\ cos^2\alpha}}{2\sqrt{5-4\ cos\ \alpha}} . . . . . . .
(5)
Nun folgen die Coordinaten des Punktes S:
x=Ap=2\,O\,o=2\,O\,n\ cos\,\beta=2\,OR\ cos\,\gamma\
cos\,\beta,
y=pS=AO+2\,o\,n=AO+2\,O\,n\ sin\,\beta=AO+2\,OR\
cos\,\gamma\ sin\,\beta
und durch Substitution von AO=OR=2\,r und
der übrigen Werthe nach Gleichung (2), (3) und (5) ergibt sich als Endresultat:
\frac{x}{2\,r}=(2-cos\ \alpha)\,\frac{\sqrt{19-12\ cos\
\alpha-4\ cos^2\alpha}}{5-4\ cos\ \alpha} . . . . . . . (6)
und
\frac{y}{2\,r}=1+sin\ \alpha\,\frac{\sqrt{19-12\ cos\
\alpha-4\ cos^2\alpha}}{5-4\ cos\ \alpha} . . . . . . . (7)
Als Maxima und Minima von x und
y berechnen sich die Werthe:
\alpha = 0^{\circ}
\frac{x}{2\,r}=1,732
\frac{y}{2\,r}=1
24
1,750
1,66
60
1,732
2
114
1,750
1,66
180
1,732
1
246
1,750
0,34
300
1,732
0
336
1,750
0,34
Der Fehler beträgt also 1 Procent von x. Das Diagramm Fig. 18
Taf. 37 zeigt, in welcher Weise sich x und y mit fortschreitender Drehung der Kurbel ändern.
Hamburg a. Donau, 11. Februar 1883.
Tafeln