| Titel: | Beiträge zur Geschichte, Theorie und Praxis der Zeicheninstrumente, insbesondere der Ellipsographen; von Prof. Ernst Fischer. |
| Autor: | Ernst Fischer |
| Fundstelle: | Band 255, Jahrgang 1885, S. 188 |
| Download: | XML |
Beiträge zur Geschichte, Theorie und Praxis der
Zeicheninstrumente, insbesondere der Ellipsographen; von Prof. Ernst Fischer.Nach einem im Münchener Architekten- und Ingenieurverein gehaltenen
Vortrage.
Mit Abbildungen auf Tafel
14 und 20.
Ernst Fischer, über Zeicheninstrumente.
Um eine umfassende Geschichte der Zeicheninstrumente zu schreiben, dürften die Kräfte
eines Einzelnen wohl kaum ausreichen. Bei der Massenhaftigkeit des einschlägigen
Stoffes, welcher zudem erst in neuester Zeit einigermaſsen zusammengetragen und
geordnet ist, wozu insbesondere verschiedene AusstellungenVgl. Bericht über die Ausstellung wissenschaftlicher
Apparate im South Kensington Museum zu London 1876. Zugleich
vollständiger und beschreibender Katalog der Ausstellung. Im Auftrage des
kgl. groſsbritannischen Erziehungsrathes zusammengestellt von Dr. Rud. Biedermann. (London 1877.) – Bericht über die wissenschaftlichen Apparate auf der
Londoner internationalen Ausstellung 1876, herausgegeben von A. W. Hofmann. (Braunschweig 1878. Vieweg und Sohn.) – Internationale Ausstellung in
London 1876. Handbuch u.s.w. von R.
Biedermann. (London 1876.) beigetragen haben, kann sich
daher auch der Verfasser des vorliegenden Berichtes nur darauf beschränken, ein
ziemlich unvollständiges Bild dessen zu geben, was der obige Titel dieser Abhandlung
zu versprechen scheint. Freilich lag auch die Versuchung nahe, gleich die Geschichte
der Recheninstrumente mit in den Kreis unserer Betrachtungen zu ziehen- denn:
„Lineal und Zirkel“, es ist das Losungswort, wenn wir zurückschauen bis
zu den Anfängen der Kunst und der Technik; und wie nahe steht dem Lineale der
Maſsstab und es dient der Zirkel nicht bloſs zum Beschreiben von Kreisen, sondern
auch zum Messen von Längen. Wo also soll man die Grenze ziehen, zwischen einer
Beschreibung von Zeichenapparaten und einer solchen von Recheninstrumenten? Was die
letzteren betrifft, so denke man nur an die verschiedenen Formen von Rechenschiebern, welche
sich an die Betrachtung der Maſsstäbe schon deshalb anschlieſsen, weil sie selbst
nichts anderes sind, als an einander verschiebbare, je nach den besonderen Zwecken
getheilte Stäbe; dann erst die vielen Rechentafeln und Diagramme, der Abakus und die
Rechenmaschinen, die KreistheilungUeber die Geschichte der Kreistheilung vgl. Klügel's mathematisches Wörterbuch.
(Leipzig 1803/36.) u.s.w., für welche Gegenstände sich reichlich
historischer Stoff bietet, so daſs diese Aufgabe gewiſs eine dankbare wäre.
Lineal und Zirkel – die beiden hauptsächlichsten Instrumente für geometrisches
Zeichnen und Construiren – stammen aus dem fernsten Alterthume. Wahrscheinlich war
eine gespannte Schnur, wie dieselbe noch heutzutage bei den Zimmerleuten in Gebrauch
ist, die Urform der Vorrichtung, um eine gerade Linie zu erlangen, und eine an einem
Pflocke befestigte Schnur (eine Einrichtung, die von den Gärtnern zum Abstecken
kreisrunder Beete noch heute benutzt wird) gewährte zuerst das Mittel, einen Kreis
zu beschreiben. Zirkel, wie wir dieselben jetzt benutzen, und zwar einige von sehr
verschiedenen Formen, sind bei den Ausgrabungen von Pompeji gefunden worden.
Wahrscheinlich ist jedoch, daſs die Anwendung des Zirkels, welche jetzt allgemein
ist, Längen mit Genauigkeit von einem Maſsstäbe auf eine Zeichnung oder von einer
Zeichnung auf eine andere zu übertragen, schwerlich im Alterthume ausgeübt wurde.
Wäre diese Anwendung im Gebrauche gewesen., so ist schwer einzusehen, warum dieselbe
nicht das zweite und dritte Problem des Euklid, in
welchen Längen durch wirkliches Schlagen von Kreisen übertragen werden, bei Seite
geschoben hat.
Was nun die Geschichte der Zeicheninstrumente betrifft, so zeigt sich dieselbe schon,
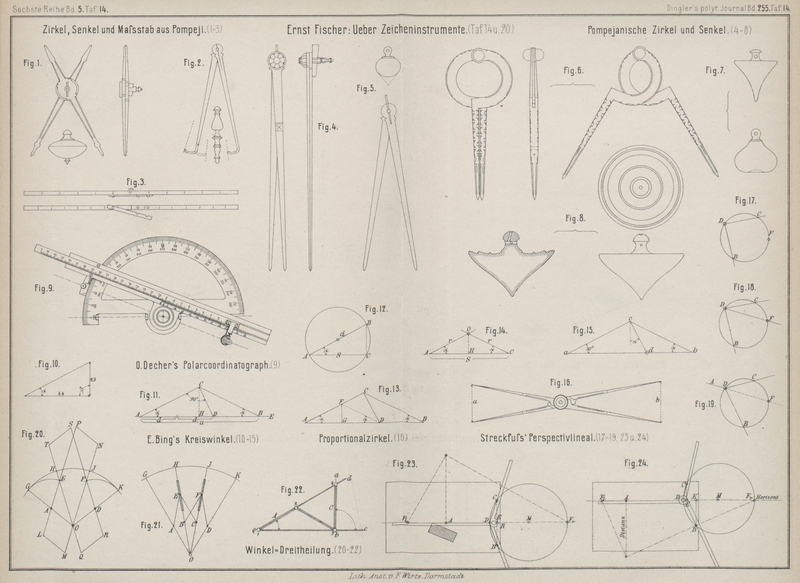
wenn man nur das wirklich Vorhandene in Betracht zieht. Die Figuren 1 bis 3 Taf. 14
dürften wohl das ältest Vorhandene auf dem vorliegenden Gebiete darstellen; es sind
Gegenstände, welche sich bei den Ausgrabungen von Pompeji vorgefunden haben.Vgl. J. Overbeck: Pompeji (Leipzig 1866) Bd. 2
S. 87. Wollten wir den bildlichen Stoff für diesen Gegenstand aus
Gemälden entnehmenVgl. Perrot et Chipiez: Histoire de
l'Art., so würden wir hier eine sehr bedeutende Reihe vorführen
können, welche, bei den Schreibmaterialien beginnend, bis zu den Werkzeugen
eigentlicher Kunst aufsteigen würde. Doch wir wollen uns nur auf das wirklich
Vorhandene beschränken. Vollständig aufgefunden sind die Werkzeuge hervorragender
Bildhauer und Steinmetzen, welche in allem Wesentlichen durchaus dieselben sind, wie
man sich ihrer noch heute bedient. Nur einen Zirkel,
welcher bei der Bildhauerei diente, theilen wir unter der kleinen Auswahl von
pompejanischen Meſsgeräthen mit, welche in Fig. 1 bis 3 Taf. 14 wiedergegeben
sind, und der dem heutigen so ähnlich ist, wie ein Ei dem anderen, was übrigens das
Interesse an diesen
Gegenständen nicht vermindern kann. Wir finden in Fig. 3 einen zusammenlegbaren Maſsstab von einem römischen Fuſs,
welcher durch Punkte auf der einen Seitenfläche in 12 Uncien, durch Punkte auf der
unteren Kante in 16 Digiti, die beiden gewöhnlichen Eintheilungen des Fuſses,
getheilt ist. Den kleinen Halter, durch welchen der aus einander gelegte Maſsstab
gesteift wird, bemerkt und versteht man wohl sofort aus der Zeichnung. In Fig. 1 ist ein
Halbirungszirkel dargestellt, innerhalb dessen
Schenkeln wir ein Bleigewicht (Senkblei, Loth, perpendiculum) gröſseren Kalibers, sowie zwischen den Schenkeln des.
Zirkels Fig. 2
ein solches kleineren Kalibers und von zierlicherer Gestalt gezeichnet haben. Der
aus der Bildhauerwerkstätte stammende Zirkel
Fig. 3 hat
gebogene Spitzen, von denen die eine lose ist, und diente zur Messung von krummen
Flächen und zwar mit nach innen gekehrten Spitzen zur Messung convexer, mit nach
auſsen gekehrten Spitzen zur Messung concaver Gegenstände. Zum Verständnisse der
Anwendung müssen wir noch bemerken, daſs die beiden Schenkel wie die Schneiden einer
Schere neben einander liegen, so daſs der jetzt rechts befindliche Schenkel links,
der sich links befindende rechts stehen konnte, in welcher Stellung sodann durch
Umdrehen der einen Spitze die beiden Spitzen einander zugekehrt waren. – Dieselbe
Einrichtung der Lage zweier Schenkel in zwei Ebenen zeigt die Seitenansicht des
Halbirungszirkels Fig. 1, über den wir nur noch bemerken wollen, daſs derselbe in jeder
Weite durch eine Stellschraube festgestellt werden konnte.
Was die folgende Gruppe von Figuren 4 bis 8 Taf. 14
betrifft, so haben wir dieselben nach den im kgl. Antiquarium zu München
befindlichen antiken Zirkeln und Senkeln angefertigt. Einer dieser Zirkel (Fig. 6) bietet
besonderes Interesse, sowohl durch seine Gestalt, als auch durch seine Ausstattung.
Dieser Zirkel wurde schon im J. 1867 in Carl's Repertorium, Bd. 3 S. 65 Taf. V, doch nicht mit der
nöthigen Sorgfalt abgebildet; aber der ungenannte Berichterstatter bleibt auch
insofern zurückhaltend, als er den Zirkel in seinem zerbrochenen Zustande darstellt
und es dem Beschauer überläſst, sich den abgebrochenen Theil als solchen, oder als
Constructionseigenheit zu denken; ferner wird dort nur mitgetheilt, daſs besagter
Zirkel durch Prof. Brunn aus Rom mitgebracht und an das
hiesige Antiquarium verkauft wurde und daſs derselbe gewiſs groſses historisches
Interesse erwecke. – Wir waren nun anfänglich auch der Meinung., daſs der später von
uns als abgebrochen erkannte Theil besonderen Zwecken
gedient habe: allenfalls die Halbirungsrichtung eines aufgetragenen oder
abgegriffenen Winkels zu geben; allein wir kamen von dieser Idee wieder ab, nachdem
wir die vorhandenen Bruchflächen erkannt hatten, und gelangten zu der Ueberzeugung,
daſs hier nur ein einfacher Zirkel vorliege und daſs man zur Zeit, als dieser Zirkel
construirt wurde, eben den gelenkartigen Theil desselben nur durch Anlöthen eines
besonderen Stückes herzustellen vermochte.
Auch die übrigen Stücke aus dem kgl. Antiquarium zeichnen sich durch eine fein
empfundene Ornamentirung aus, insbesondere noch ein Zirkel Fig. 4 und der gröſsere
Senkel Fig. 8,
dessen Profil auch deshalb dargestellt wurde, um noch die eigenartige Bohrung des
Kopfes zu zeigen. Bemerkenswerth bei diesem Senkel ist besonders die Profillinie des
Mantels, dem griechischen Echinus ähnlich gestaltet.
Im kgl. Antiquarium haben wir auch die verschiedensten Griffel und Stäbchen gesehen;
dieselben, aus Bronze hergestellt, sind meist hübsch verziert, ähnlich unseren
gedrechselten Federhaltern; die gebrauchten Enden sind häufig abgebrochen; unter den
noch erhaltenen Griffeln sind solche mit etwa 5mm
breiten Schneiden, deren Zweck wahrscheinlich darin bestand, in der fein quadrirten
Wachsfläche Mauer- und Pilasterstärken für Grundschnitte sanft einzudrücken; auch
ist es nicht unwahrscheinlich, daſs die Kantenbreite je nach der Wahl des Maſsstabes
der Zeichnung 1 Modul oder 1 Partes entsprach. Andere derartige Griffel, von uns
Schaber genannt, schienen uns anfänglich, ähnlich den heutigen Falzbeinen, zum
Glätten der auf den Wachstafeln falsch dargestellten Linien gedient zu haben; durch
deren gröſsere Aehnlichkeit aber mit unseren Bossirhölzern haben wir uns der Ansicht
zugeneigt, daſs diese Gegenstände aus Bildhauerwerkstätten stammen. Der
altgriechischen Sage nach wurden ohnedies Zeichnung und Plastik zugleich erfunden
und als die erste Zeichnerin wird die Tochter des Dibutades genannt, welche den Schatten des Profiles ihres scheidenden
Gemahles an der Wand umschrieb, den der Vater dann ausschnitt und in Thon
modellirte. Ardices und Telephanes, wahrscheinlich erdichtete Namen, sollen es gewesen sein, die
durch Schraffirung die Rundung der Körper auszudrücken suchten. Philokles und Kleanthes
erfanden die Monochromen, d. s. die einfachen farbigen Zeichnungen, bei welchen die
Farben durch Beigabe von Weiſs verschiedene Töne erhielten. Die Griechen waren sehr
streng beim Unterrichte im Zeichnen; Pamphilus, der
Lehrer des Apelles, verlangte, daſs seine Schüler zehn
Jahre bei ihm lernten. Die Linearzeichnung wurde bei den Griechen zur höchsten
Vollkommenheit gebracht und bekannt ist der Wettstreit des Apelles und Protogenes in solchen mit
ungemeiner Zartheit hingeworfenen linearen Figuren.
Zu den Griffeln zählen auch ferner die pinselartigen Formen, wie dieselben sich
bereits auf alten egyptischen Darstellungen finden, wie es überhaupt bei den alten
Völkern beliebt war, ihre Meister auf Bildern und Reliefs mit deren Handwerkszeug,
arbeitend, darzustellen. Unter allen Stiften fand der Röthel, besonders bei den
Griechen, frühzeitig die meiste Anwendung; mit demselben läſst sich bekanntlich
besonders auf Marmor gut zeichnen.
Die vorangehende Betrachtung führt uns übrigens von selbst auf einige Mittheilungen,
welche, im engen Zusammenhange mit unserem Thema stehend, über das zur Herstellung der Zeichnungen
gebrauchte Material zu machen sind. So weit unsere Forschungen reichen, waren es die
Phönizier, welche kurz vor dem Solon'schen Zeitalter
damit anfingen, die Töne des Gesprochenen aufzuzeichnen, im Gegensatze zur
Hieroglyphie. Zu beiden gehörten aber schon eigene Stifte oder Stäbchen, als die ersten
Werkzeuge, um Zeichnungen festzulegen. Der Sage nach soll Kadmus dieses Verfahren von den Phöniziern zu den Griechen gebracht haben,
von welchen es wieder die Etrusker und die Römer sich aneigneten. Als Zeichenfläche
diente anfangs Stein, Thon, Metall, Wachs, Baumrinde. Die äuſserst genauen
Tempelzeichnungen der Griechen wurden gewiſs mit scharfen Bronzestiften in
Metallflächen oder auf polirtem Stein in Gravur ausgeführt. Von den Zeichnungen zu
egyptischen Tempeln fehlen uns alle Anhaltspunkte. Im 3. Jahrhunderte v. Chr. tritt
der egyptische Papyrus, dann Thierhaut, zu Pergament verarbeitet, auf; im 8.
Jahrhunderte n. Chr. das Baumwollpapier und seit dem 14. Jahrhunderte das Leinen-
und Lumpenpapier. Auſser den Meiſseln, Griffeln und Sticheln der Griechen und Römer
tritt dann allmählich der Pinsel, das Rohr und später die starke Flügelfeder
gröſserer Vögel auf, bis endlich die Stahlfeder auch diese auf ein enges
Anwendungsgebiet beschränkte. Als ganz neu dürfen die aus Glas hergestellten
Schreib- und Zeichenfedern betrachtet werden; dieselben sind zu Spitzen fein
ausgezogene Glasröhrchen, welche dann abgebrochen und auf den gewünschten
Durchmesser fein abgeschliffen werden. Man füllt diese Federn mit leichtflüssiger
reiner Tinte oder mit körnerfreier Tusche und kann dann damit ein paar Stunden
schreiben oder zeichnen, wobei der gleichmäſsige Strich, beispielsweise von hohem
Werthe beim Zeichnen von Horizontalcurven, beachtenswerth ist. Diese Federn dürften
sich auch für Registrirapparate, welche eine schräge oder senkrechte Lage des
Stiftes gestatten, empfehlen.
An die vorausgehende Betrachtung lieſse sich am besten die Aufzählung der
verschiedenen Reiſszeuge anreihen; doch darf dieser Gegenstand, als zu allgemein
bekannt, nur kurz berührt werden. Von besonderem historischem Interesse ist dabei
zunächst die im J. 1876 auf der Londoner Ausstellung wissenschaftlicher Apparate
vorgeführte, dem Fürsten v. Pleſs gehörige Sammlung
mathematischer Instrumente für geometrisches und Fortifications-Zeichnen, aus den
ersten Jahrzehnten des vorigen Jahrhunderts stammend, ausgezeichnet durch
auſserordentliche Sauberkeit und vorzügliche Erhaltung. Diese Sammlung besteht aus
134 Stücken: 11 Zirkel mit 11 zugehörigen Theilen, 28 Lineale und Maſsstäbe, 2
desgleichen zum Fortificationszeichnen, mit 2 Schlüsseln, 8 Dreiecke und
Winkelhacken, 10 Winkelmesser, 2 Storchschnäbel und 52 sonstige Apparate. Gehen wir
gleich auf die neue Zeit über, so sind besonders die Leistungen des Kern'schen Institutes in Aarau (Schweiz) als
bahnbrechend hervorzuheben.
Unter den allgemein gebräuchlichen Reiſsfedern sind drei besondere Gattungen zu
erwähnen: Die im Griffe feststellbaren, federnden, dann die nicht federnden und
endlich die im Griffe drehbaren, die sogen. Curvenfedern. Der Zweck der Curvenziehfedern ist lediglich der, jede
krumme Linie genau ausführen zu können. Eine solche Feder ist von Ed. Sprenger in Berlin construirt und näher im B. p. J. 1878 227 * 529
beschrieben; bei derselben hat man nur nöthig, den Griff der Feder (nachdem dieselbe
mit Tusche oder Tinte wie jede gewöhnliche Reiſsfeder gefüllt ist) genau senkrecht
zu führen; der Stiel ist unbedingt ganz fest zu halten, da der untere Theil der
Feder von selbst jeder Bewegung des Stieles entsprechend sich in der Richtung der zu
ziehenden Curve einstellt. Um die Curvenfeder als gewöhnliche Reiſsfeder (also nur
zu geraden Linien) gebrauchen zu können, genügt es einfach, eine kleine Schraube,
die sich am Ende des geraden Halters befindet, festzuziehen, in Folge dessen die
Drehbarkeit der Feder aufgehoben wird.
Unter den Curvenlinealen gehören die von Kern in Aarau aus Bein, noch besser aus Hörn, sowie die
von Preiſsinger in München angefertigten Heindl'schen zu den empfehlenswerthen; alle übrigen uns
bekannt gewordenen Formen sind zu verwerfen, indem nur die genannten die Elemente
der cyclischen Curven sowohl, als auch der Voluten und der Kegelschnitte geben.
An neueren Verbesserungen geometrischer Apparate sind anzuführen:
1) Der Proportionalitäts- oder Reductionszirkel, welcher es ermöglicht, eine gegebene Länge, welche von
einer Zeichnung auf eine andere übertragen werden soll, in einem bestimmten
Verhältnisse zu vergröſsern oder zu verkleinern, um eine der gegebenen ähnliche
Figur zu erhalten;
2) der Dreispitzzirkel, durch welchen die Lage von drei
ein Dreieck bildenden Punkten von einer Zeichnung auf eine andere übertragen werden
kann und welcher somit zum Uebertragen von Winkeln geeignet ist; 3) der Stangenzirkel, bestehend aus einer mit sehr genauer
Theilung versehenen Stange oder Schiene, an welcher entlang die beiden Spitzen des
Instrumentes vor- und rückwärts bewegt werden können. Der Abstand derselben kann
mittels einer Mikrometerschraube mit groſser Genauigkeit eingestellt werden. In der
Allgemeinheit seiner Anwendung für geometrisches Planzeichnen folgt zunächst der in
gleiche Theile getheilte Maſsstab. Man theile ein Paar gegenüber liegende Seiten
eines Rechteckes z.B. in 10 gleiche Theile und beziffere die Theilpunkte mit 1, 2,
3,.... 9, ziehe hierauf die Linien 1-1, 2-2, 3-3,.... 9-9 parallel den Seiten des
Rechteckes; das andere Paar von gegenüber stehenden Seiten des Rechteckes sei in
ähnlicher Weise in 10 gleiche Theile getheilt, die Theilpunkte seien aber in
schräger Richtung durch die Parallelen 0-1, 1-2, 2-3... mit einander verbunden; man
wird dann linden, daſs die erste Gruppe von Parallelen durch die zweite in Hundertel
getheilt wird. Ein solcher Diagonalmaſsstab ist auf
jedem sogen.
Zeichenmaſsstabe aufgetragen und dient dazu, einen der ursprünglichen Theile in
Hundertel zu theilen. Mit einem feinen Zirkel läſst sich von dem Maſsstabe jede
verlangte Länge abgreifen, mit einem Fehler, der ein 1/500 der Grundtheilung nicht
überschreitet.
Schleicher und Schüll in Düren
liefern in neuester Zeit Transversalmaſsstäbe in 24 verschiedenen Theilungen in
bisher nicht erreichter Genauigkeit auf Papier gedruckt. (Der Preis ist 15 Pf. das
Stück.) Das dazu verwendete Papier ist nicht dehnbar, eine Veränderung daher
ausgeschlossen. Rühmlichst bekannt sind die von Beck und
Nestler in Lahr aus Holz und Bein hergestellten Maſsstäbe, besonders
empfehlenswerth jene mit linsenförmigem Querschnitte. An dieser Stelle möge die
Bemerkung eingeschaltet werden, wie überraschend es ist, daſs keine Maſsstabfabrik
prismatische Maſsstabe herstellt, bei denen die Theilungen auf beiden Seiten mit
entgengesetzten Bezifferungen beginnen, welche Einrichtung doch besondere
Bequemlichkeiten bietet. Beck und Nestler liefern auch
sogen. Stellschienen, sowohl mit einfachem, als auch
mit doppeltem Anschlage und auch zum Verstellen mittels Kreisbogen.
Eine weiter durchgebildete Reiſsschiene mit Winkelmesser und
Neigungsskala hat Hotop construirt; dieselbe
ist im D. p. J. 1876 222 *
534 beschrieben, daher hier nur darauf hingewiesen sei.
Zur besten und bequemsten Lösung der Aufgabe: Einen Winkel zu
construiren, welcher einem gegebenen Winkel gleicht, nehmen wir getheilte
Kreise oder Theile von Kreisen zu Hilfe, wie sie als Kreis-,
Halbkreis- oder Quadranten-Uebertrager bekannt
sind. Die einfacheren Uebertrager sind jene von Kern in
Aarau, mit Arm und Nonius; die vollendetsten sind die vom Privatdocenten Dr. Otto Decher in München construirten, welche derselbe
mit dem Namen Distanzentransporteur oder Polarcoordinatograph bezeichnet hat. Dieser in Fig. 9 Taf. 14
dargestellte Apparat dient zum gleichzeitigen Auftragen von Winkeln und wagerechten
Entfernungen (Polarcoordinaten), wie sie durch tachymetrische Aufnahmen erhalten
werden, gleichviel mit welcher Art von Universalinstrumenten, diese ausgeführt sind.
Der Distanzentransporteur bildet somit eine nothwendige Ergänzung der Meſsapparate
letzterer Art zum Zwecke der graphischen Darstellung der Aufnahmen.
Der Auftrageapparat, kurz Auftrager
genannt, besteht aus einem gewöhnlichen Halbkreistransporteur mit doppelt
bezifferter Kreistheilung von 10cm Radius und
einem Lineale von 28cm Länge mit ebenso langer
Zunge, die in nuthartiger Vertiefung genau eingepaſst und gerade geführt ist.
Halbkreis und Lineal sind in ihrer Mitte durch flache, ringartige Ansätze so
verbunden, daſs ihre gegenseitige Bewegung genau und doch leicht um eine
gemeinschaftliche Achse ermöglicht ist. Die Lage dieser Drehachse auf der
Auftragebene (Zeichenfläche) ist in der Durchbrechung der Ansätze durch ein
durchsichtiges Horn- oder Gelatinplättchen mit aufgerissenem Centrum sichtbar
gemacht.
Das Lineal trägt an einem Ende einen in der Ebene der
Kreistheilung liegenden, dieser angepaſsten Nonius von 1 Minute Angabe, der frei
über die Zeichenebene hinweggleitet. Mit diesem Nonius werden gegebene Richtungen
und Winkel eingestellt. Zum Auftragen der wagerechten Entfernungen dient die Zunge
mit der auf dieselbe aufgesetzten Punktirvorrichtung. Die Spitze der letzteren liegt
mit dem Nullstriche des vorgenannten Nonius auf einem Durchmesser, so daſs das
Centrum stets zwischen beide fällt. Diesem Durchmesser genau parallel ist die gerade
Bewegungsrichtung der Zunge. Oberfläche von Lineal und Zunge liegen in einer Ebene;
die einander gegenüber liegenden Flächenstreifen beider dienen zur Auftheilung
gewünschter Längenmaſse nach verschiedenen Maſsstäben. Der Nullpunkt der Theilung ist der Fuſspunkt einer
Senkrechten von der Spitze des Punktirstiftes auf die Theillinie. Die Theilung der
Zunge selbst erstreckt sich für Metermaſs auf eine Länge von 25cm; ihre Fortsetzung für ausnahmsweise gröſsere
Längen liegt auf dem Lineale. Zur genauen Einstellung gegebener Längen dienen zwei
Nonien, deren Angabe 0mm,1 beträgt. Der Nullstrich
des gewöhnlich zu benutzenden Nonius auf dem Lineale ist der Fuſspunkt einer
Senkrechten vom Centrum auf die Theillinie. Die Entfernung des Centrums vom
Punktirstifte wird demnach durch Einstellen der Zungentheilung gegen diesen
Nullstrich bestimmt. Für gröſsere Längen als 25cm
kommt der am linken Ende der Zunge liegende Nonius mit der Theilung auf dem Lineale
zur Verwendung, indem als Index der letzte Theilstrich der Zungentheilung (zugleich
Nullstrich des Nonius, im Originale der Theilstrich „25“) gebraucht und auf
die Linealtheilung eingestellt wird. Diese reicht bis 36cm eine Länge, welche selbst im Maſsstabe 1 : 500 noch 180m wagerechter Entfernung entspricht.
Am Auftrager befinden sich 3 Schräubchen: das eine klemmt die
Hülse des Punktirstiftes fest und läſst sonach diesen verschieden hoch stellen. Das
zweite Schräubchen mit ränderirtem Kopfe liegt im Durchmesser von Punktirspitze und
Nullstrich des Alhidadennonius, endigt in eine feine Spitze, die sich beim
Vorwärtsdrehen des Kopfes ins Papier sticht und in Verbindung mit jener des
niedergelassenen Punktirstiftes die Alhidade sammt Lineal und Zunge auf dem Papiere
festhält, während gleichzeitig der Halbkreis wenig gehoben wird und unter dem
Lineale gedreht werden kann. Das dritte Schräubchen mit versenktem Kopfe, über
welchen beim Drehen das Lineal hinweggeht, bei den Ziffern 90 bezieh. 270 der
Sexagesimalkreistheilung, endigt ebenfalls in eine feine Spitze, die sich mit Hilfe
eines Schraubenziehers ins Papier drehen läſst; dieses Schräubchen dient dazu, rasch
und sicher eine einmal gegebene Lage des Ganzen in Bezug auf einen Bildpunkt
herbeizuführen. Endlich ist die Nulllinie der Kreistheilung, die Anfangsrichtung der
Winkelzählung, gegen das Centrum hin auf den abgeschrägten kleinen Flächen noch
dreifach durch auf einem Radius liegende Marken bezeichnet, damit die Lage des
Auftragers auf einer gezeichneten Richtung immer leicht beurtheilt werden kann.
Der Gebrauch des Auftragers ist
folgender: Die Originalaufschreibungen einer tachymetrischen Aufnahme werden meist
nicht unmittelbar zum Auftragen zu verwenden sein, sondern es müssen einmal die
abgelesenen Richtungen auf eine Anfangsrichtung umgerechnet werden, sofern nicht ein
Repetitionstheodolit zur Verwendung kam, welcher die Nullablesung für die
Anfangsstellung der Visirlinie einzustellen gestattet; sodann sind erst die
Distanzen, sowie ihre Horizontal- und Vertikalprojectionen (am schnellsten mit dem
RechenschieberRechenschieber für Berechnung tachymetrischer und barometrischer Aufnahmen
nach Decher's Angaben liefert die
Maſsstabfabrik von Beck und Nestler zu Lahr in
Baden für etwa 15 M.) zu rechnen.
An die auf dem Zeichenblatte gegebene Anfangsrichtung legt man nun
zum Auftragen den Distanzentransporteur so nach einer Seite an, daſs sein
Mittelpunkt das Bild des gegebenen Stationspunktes deckt und daſs die Marken in die
Nullrichtung fallen. Der Punktirstift kommt in die gegebene Richtung, während der
Nullstrich des Alhidadennonius, sowie die Spitze des dortigen Schräubchens in deren
rückwärtiger Verlängerung zeigen, wenn auf Null der Kreistheilung eingestellt wird.
Sodann zieht man das Schräubchen bei 90° mit einem Schraubenzieher an, bis seine
Spitze ins Papier dringt; tritt nun im ferneren Gebrauche eine zufällige
Verschiebung ein, so kann diese allein eine Drehung um diese Spitze sein; man
braucht demnach nur die Deckung des Centrums mit dem Bildpunkte durch Zurückdrehen
wieder herbeizuführen, um sofort wieder die richtige Lage zu erhalten.
Es erscheint nun zweckmäſsig, beim ferneren Gebrauche zuerst die Entfernungen und dann die Winkel einzustellen. Ersteres geschieht durch einen leichten
Seitendruck auf die Hülse des Punktirstiftes mit der rechten Hand., bis der Nonius
die einzustellende Entfernung zeigt, während die linke Hand den Transporteur aufs Papier
drückt; letzteres, indem man das Lineal leicht am rechtseitigen Ende anfaſst und so
lange dreht, bis der Nonius am Kreise die gewünschte Stellung hat, worauf ein
rascher Druck auf den Kopf des federnden Punktirstiftes die Lage des gegebenen
Punktes auf das Papier sticht. (Sollte diese in Blei gezeichnet, statt punktirt
werden, so läſst sich statt des Punktirstiftes ein Zeichenstift einsetzen und ebenso
verwenden.)
Zur Vermeidung der Umrechnung der Kreisablesungen auf eine
Nullrichtung kann folgendermaſsen vorgegangen werden: Nachdem vor dem Gebrauche alle
3 Spitzen zurückgezogen sind, bringt man das Centrum mit dem gegebenen Bildpunkte
zur Deckung und den Punktirstift in die gegebene Anfangsrichtung, löst das
Klemmschräubchen des Punktirstiftes und drückt diesen ins Papier; sodann wird das
zweite Schräubchen am Alhidadennonius angezogen, bis seine Spitze fest im Papiere
sitzt. Hierdurch erhält der Halbkreis hinreichend Spielraum, so daſs man denselben
drehen und auf jene Ablesung einstellen kann, welche für die Anfangsrichtung gegeben
ist. Endlich wird das dritte Schräubchen ebenfalls angezogen, bis seine Spitze im
Papiere festsitzt, die beiden ersteren Schräubchen werden zurückgedreht und man hat
nun unmittelbar die bei der Aufnahme erhaltenen Ablesungen am Kreise auf dem
Auftrager einzustellen, um die Richtungen in ihrer gegenseitigen Lage auf dem
Papiere zu erhalten.
Sind sämmtliche auf eine Hälfte des Kreisumfanges treffenden
Richtungen und Punkte aufgetragen, so wird das Instrument umgelegt, indem dasselbe
auf die andere Seite der Anfangsrichtung mit vertauschter Lage für Punktirstift und
Nonius angelegt wird und sodann die zweite Bezifferung der Kreistheilung zu benutzen
ist. Im Allgemeinen ist es vortheilhaft, die Zeichenebene so vor sich zu legen, daſs
die Anfangsrichtung als Senkrechte erscheint, an welcher der Auftrager links liegt,
während die rechte Seite zur Ausarbeitung gelangt.Der Auftrager aus Neusilber mit Sexagesimal- oder Centesimalkreistheilung und
beliebiger Längentheilung ist um den Preis von etwa 90 M. vom Reichenbach'schen mathematisch-mechanischen
Institute, Firma T. Ertel und Sohn in München
zu beziehen.
Zu dem Kapitel „Lineal und Zirkel“ gehören, auſser den verschiedenen Formen
von Dreiecken mit 45°, 60° und 30°, auch jene mit Neigungen von ½-maliger,
1½-maliger und ¾-maliger Böschung, wie man sich dieselben zur Zeichnung vieler Damm-
oder Einschnittsprofile beim Entwürfe von Erdbauwerken herstellen läſst. Ferner muſs
hier eines Dreieckes gedacht werden, das unter den Hunderten von Lösungen für die
graphische Quadratur des Kreises wohl die beste und empfehlenswertheste geben
dürfte. Das Instrument, von J. Schröder in Darmstadt in
zwei Gröſsen zu beziehen, ist nach seinem Erfinder der Bing'sche Kreiswinkel benannt und hat das
Aussehen eines gewöhnlichen Winkeldreieckes.
Die Aufgabe, die Abwickelung eines Kreisumfanges auf eine gerade Linie oder die
Verwandlung einer Kreisfläche in ein gleich groſses Quadrat durch eine einfache
Construction ohne Rechnung genau vorzunehmen, hat seit undenklichen Zeiten als
unlösbar gegolten und ist es gewissermaſsen bis heute noch. Das Bedürfniſs einer
solchen einfachen Verwandlungsconstruction tritt in neuerer Zeit noch mehr in den
Vordergrund, da die graphische Darstellung in vielen technischen Zweigen die bisher
meist übliche analytische Methode verdrängt, indem erstere meist weniger
theoretische Vorkenntnisse erfordert und zugleich ein übersichtliches Ergebniſs liefert. Die
Genauigkeit der graphischen Darstellung hängt freilich von der mehr oder weniger
scharf ausgeführten Zeichnung und gleichzeitig von der Güte der angewendeten
Instrumente (Zirkel, Winkel u. dgl.) ab.
Ed. Bing, technischer Direktor der russisch-baltischen
Waggonfabrik zu Riga, hat nun zu seiner Lösung der vorhin genannten Aufgaben, auſser
Reiſschiene (oder Anlegewinkel) und Kreiszirkel, nur einen einfachen Winkel (Dreieck
Fig. 10
Taf. 14) nöthig, bei welchem Winkel β = 90° und Winkel
α = 27°35'49'',636 ist, oder mit anderen Worten: Es
muſs cos α = ¼π sein. (Es
läſst sich dieser Winkel a auch aus seiner Tangente
construiren, welche fast genau = 23/44 ist.) Wenn die nachfolgende Constructionsmethode
erst in weiten Kreisen bekannt sein wird, so werden solche Winkel, welche sich
fabrikmäſsig ja fast mit mathematischer Genauigkeit herstellen lassen, überall in
verschiedenen Gröſsen im Handel zu haben sein. In Folgendem geben wir die mit dem
Kreiswinkel zu lösenden Aufgaben nebst Beweisen.
1a) Der Durchmesser d eines Kreises
ist gegeben- man soll den Umfang u construiren.
Lösung: Auf Linie AE (Fig. 11 Taf. 14) trage
man AD = 2d auf, lege die
Hypothenuse des Kreiswinkels an die Reiſsschiene und ziehe mit der langen Kathete
AC, mit der kurzen DC,
kehre den Kreiswinkel um und ziehe mit demselben durch C die Linie CB, so schneidet diese den Umfang
u = AB auf der Linie AE ab.
Beweis: Ziehe die Höhe HC, so ist
A\,C\,:\,A\,D=cos\,\alpha=\sqrt{1/4\,\pi}; ferner
A\,H\,:\,A\,C=cos\,\alpha=\sqrt{1/4\,\pi}. Multiplicirt man
diese beiden Gleichungen mit einander, so entsteht: AC
: AD × AH : AC = ¼π oder AH : AD = ¼π oder 4AH = AD × π. Da nun AD = 2d und 2AH = AB ist, so
folgt: 2AB = 2dπ oder AB = dπ; somit ist AB = u
der gesuchte Umfang.
1b) Der Umfang u eines Kreises ist
gegeben, man soll den Durchmesser d construiren.
Lösung: Trage in Fig. 13 Taf. 14 AB = u auf, ziehe AC und
BC mit dem Kreiswinkel, sodann aus dem
Durchschnittspunkte C die Linie CD ebenfalls mit dem Kreiswinkel, so schneidet diese AD = 2d auf der Linie AB ab. Will man ohne Zirkeltheilung das einfache d finden, so ziehe man DF
ebenfalls mit dem Kreiswinkel, fälle vom Durchschnittspunkte F ein Perpendikel auf AB, welches AG = d auf der Linie AB
abschneidet.
Der Beweis ist ganz ähnlich wie vorhin zu führen.
2a) Es ist ein Kreis bezieh. dessen Durchmesser d gegeben; es soll die Seite S des Quadrates construirt werden, welches gleich groſse Fläche wie der
Kreis hat.
Lösung: Man lege die kurze Kathete des Kreiswinkels an die
Reiſsschiene und ziehe im Kreise (Fig. 12 Taf. 14) den
Durchmesser AB mit der Hypothenuse des Kreiswinkels,
sodann mit der langen Kathete AC, so ist dies die
gesuchte Quadratseite S.
Beweis: Vollende das rechtwinklige Dreieck ABC, so ist A\,C\,:\,A\,B=A\,C\,:\,d=cos\,\alpha
=\sqrt{1/4\,\pi} also:
A\,C=d\,\times\,\sqrt{1/4\,\pi}. Quadrirt man diese
Gleichung, so entsteht AC2 = ¼πd2
; also ist AC = S die
gesuchte Quadratseite.
2b) Es ist die Quadratseite S gegeben
und es soll der Durchmesser d oder der Halbmesser r des Kreises construirt werden, dessen Fläche = S2 ist.
Lösung: Man mache AC (Fig. 14 Taf. 14) gleich
der Bekannten S, ziehe von A und C mit dem Kreiswinkel zwei Linien AO und CO, so ist deren
Durchschnitt O der Kreismittelpunkt und AO = CO = r gleich dem gewünschten Halbmesser.
Beweis: Ziehe OH senkrecht AC, so ist AH = HC = ½S; ferner ist:
1/2\,S\,:\,A\,O=cos\,\alpha=\sqrt{1/4\,\alpha}=1/2\,\sqrt{\pi}
oder S:AO=\sqrt\pi oder S=AO\times \sqrt\pi.
Quadrirt man letztere Gleichung, so ergibt sich:
S^2=\overline{A\,O^2}\,\times\,\pi; folglich ist AO gleich dem gesuchten Halbmesser r.
Wie leicht einzusehen, lassen sich die vier Aufgaben mittels des Kreiswinkels auch
auf andere Art lösen und beweisen; doch sind hier die einfachsten Lösungen und
Beweise gewählt. Die Lösungen, mit Ausnahme des Falles 2a erfordern nicht einmal
einen Kreiszirkel. Es ist ferner klar, daſs sich auf ähnliche Weise alle die
Aufgaben, welche Berechnungen mit Faktoren wie π, √π, π2 erfordern, wie
z.B. Flächenermittelung der Ellipse, mittels des Kreiswinkels lösen lassen.
Die Lösung der anfangs erwähnten, scheinbar höchst schwierigen Probleme ist somit
eine überraschend einfache und jedenfalls nicht umständlicher als das Nachschlagen
der betreffenden Zahlen in Tabellen. Bing zweifelt
deshalb nicht daran, daſs sein Kreiswinkel, welcher ja auch als gewöhnlicher
Zeichenwinkel zu gebrauchen ist, bald auf jedem Zeichentische zu finden sein
wird.
Es lassen sich die eben angegebenen Lösungen auch mittels eines anderen Instrumentes
auf noch einfachere Art und Weise finden und zwar durch einen Proportionalzirkel (Fig. 16 Taf. 14), dessen
Schenkel das Verhältniſs a\,:\,b=1\,:\,\sqrt{1/4\,\pi} haben
(annähernd = 879 : 779). Die Handhabung eines solchen Zirkels ist einfach.
1a) Stelle die Zirkelseite a auf den
gegebenen Durchmesser d, steche sodann
b=d\,\sqrt{1/4\,\pi} auf dem Papiere ab, stelle dann die
Zirkelseite a auf diese gefundene Gröſse
d\,\sqrt{1/4\,\pi}, so steht b
auf d\,\sqrt{1/4\,\pi}\,\times\,\sqrt{1/4\,\pi}=1/4\,\pi\,d;
trägt man nun b viermal auf dem Papiere auf, so ist
dies gleich dπ, d, i. der gesuchte Umfang u.
1b) Ist in umgekehrter Richtung wie la vorzunehmen.
2a) Stelle die Zirkelseite a auf den
gegebenen Durchmesser d, so ist die Zirkelseite
b=d\,\sqrt{1/4\,\pi} gleich der gesuchten Quadratseite S.
2b) Stelle die Zirkelseite b auf die
gegebene Quadratseite S, so ist
a=S\,:\,\sqrt{1/4\,\pi} gleich dem gesuchten Durchmesser d.
Wenngleich die Lösungen mit dem Proportionalzirkel einfacher als mit dem
Kreiswinkel„Bing's Kreiswinkel“ werden in zwei
Gröſsen, sowohl in Holz als in Hartgummi, von J.
Schröder in Darmstadt geliefert. sind, so werden doch
die Anschaffungskosten des ersteren, sowie die durch unvermeidliches Nachschleifen
entstehenden Ungenauigkeiten seiner allgemeinen Einführung etwas hinderlich sein,
während die Richtigstellung des Kreiswinkels ohne jede Schwierigkeit jederzeit
vorgenommen werden kann.
Schlieſslich möge noch bemerkt werden, wie die Construction des goldenen Schnittes mittels des Winkels von 30° und des Kreiswinkels
vorgenommen werden kann.
Die Theilung einer Linie ab (Fig. 15 Taf.
14) in zwei Theile derart, daſs der gröſsere Theil ad
die mittlere Proportionale zwischen dem kleineren Theile db und der ganzen Linie ab ist, d.h. die
Theilung nach dem goldenen Schnitte, kann auf folgende Weise geschehen: Man zieht
ac mit einem Winkel von 30°, die Linie bc mit dem Kreiswinkel, alsdann von dem Schnittpunkte
c die Linie cd
ebenfalls mit dem Kreiswinkel, so schneidet diese die ganze Linie ab im goldenen Schnitt. Die trigonometrische Probe
ergibt einen Fehler von 0,000568 = 1/1761 der ganzen Linie, ein Fehler, der so
geringfügig ist, daſs derselbe für das Ergebniſs ganz unwesentlich erscheint, und
welcher bei der bekannten üblichen umständlicheren Construction selbst bei feinster
Ausführung der Zeichnung nicht vermieden werden kann.
(Fortsetzung folgt.)