| Titel: | Beiträge zur Geschichte, Theorie und Praxis der Zeicheninstrumente, insbesondere der Ellipsographen; von Prof. Ernst Fischer. |
| Autor: | Ernst Fischer |
| Fundstelle: | Band 255, Jahrgang 1885, S. 217 |
| Download: | XML |
Beiträge zur Geschichte, Theorie und Praxis der
Zeicheninstrumente, insbesondere der Ellipsographen; von Prof. Ernst
Fischer.
(Fortsetzung der Abhandlung S. 188 d.
Bd.)
Mit Abbildungen auf Tafel
14 und 20.
Ernst Fischer, über Zeicheninstrumente.
An Linealinstrumenten sind nun zunächst zwei
Constructionen zu erwähnen, welche zur Dreitheilung eines
Winkels dienen und von D. Matte und Warren-Holden im Scientific
American, 1877 Bd. 36 S. 36 mitgetheilt wurden.
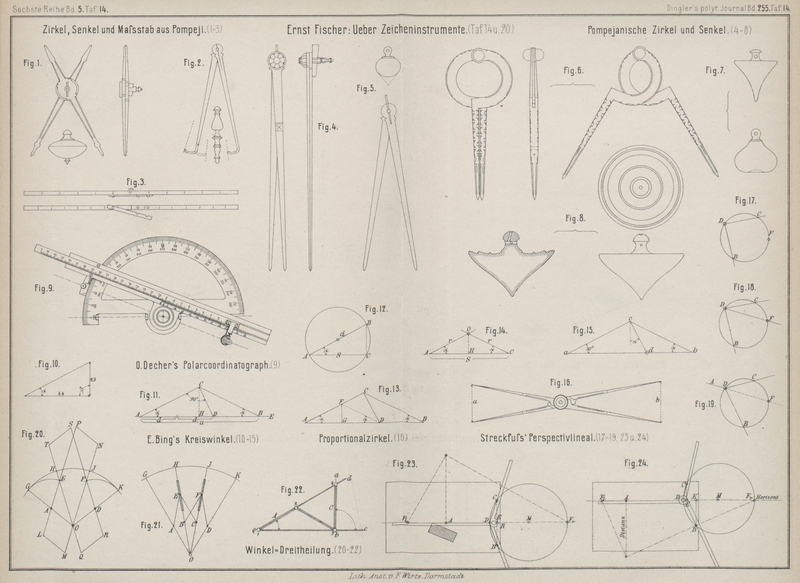
Die eine Lösung Fig. 22 Taf. 14 ist auf
den ersten Blick verständlich; die Breiecke 1 2 3 und
2 3 4 sind gleichschenklig, der Winkel 2 1 3 oder der demselben gleiche doc ist gleich ⅓abc.
Der Gebrauch des Instrumentes ist folgender: abc sei der gegebene Winkel, von welchem der dritte
Theil gewünscht wird; man verlängere den Schenkel bc in
der Richtung nach o, lege das mit C bezeichnete Lineal an die Linie ba an, halte das Instrument mit einer Hand fest und
bringe mit der anderen Hand das Ende des Lineales A in
die verlängerte Geradere, so ist od die gewünschte
Richtung.
Bei der anderen Lösung besteht der Apparat aus einem Paare
zusammengesetzter Zirkel mit 4 Beinen, welche so mit einander verbunden sind, daſs
in jeder Stellung des Zirkels das zweite Bein den Winkel halbirt, welcher durch das
erste und dritte Bein gebildet wird, während gleichzeitig das dritte Bein den Winkel
halbirt, welchen das zweite und vierte Bein mit einander einschlieſsen; auf diese
Weise wird der Winkel zwischen dem ersten und vierten Beine in 3 gleiche Theile
getheilt.
In Fig. 21 Taf. 14 sind OG, OH, OJ und OK die 4
Beine des Zirkels. AE, CE, BF und DF sind stangenförmige Verbindungsglieder, drehbar und
feststellbar in A, B, C und D, verbunden mittels Stiften in E und F, welche in Schlitzen der Beine OH und OJ gleiten können.
In den Dreiecken OAE und OCE ist OA = OC, AE =
CE und OE ist gemeinschaftlich; folglich ist
Winkel GOH = Winkel HOJ.
In derselben Weise findet sich, daſs Winkel HOJ =
Winkel JOK ist. Es sind daher die 3 Winkel einander
gleich.
Man hat also beim Gebrauche des Instrumentes nur die Seiten OG und OK auf die Schenkel
des gegebenen Winkels zu legen, die Punkte H und J zu markiren, schlieſslich HO und JO zu ziehen. Diese Construction setzt
eine Methode der Dreitheilung eines Winkels voraus durch zwei Paare von parallelen
Linealen (vgl. Fig.
20 Taf. 14). Mache OA = OD und mit derselben
Gröſse als Radius und den Mittelpunkten A und D beschreibe zwei Bögen. Der Punkt E auf der Linie OH wird
durch den einen Bogen gefunden und der Punkt F auf der
Linie OJ durch den anderen. Steche Nadeln in O, A und E, bringe die
inneren Kanten des Parallelogrammlineales LMNP gegen
die Nadeln in A und O, in
der gleichen Weise das Parallellineal QRST an die
Nadeln in O und D, bewege
dann die Lineale, dieselben gegen die Nadeln haltend, herum, bis LP die Linie QT auf dem
einen und MN die Linie RS
auf dem anderen der zuerst beschriebenen Bögen schneidet, ziehe hierauf die Gerade
längs QT und MN, womit der
Winkel dreigetheilt sein wird.
Es ist leicht einzusehen, daſs LP und
RS sich auch auf der Halbirungslinie des gegebenen
Winkels schneiden, eine Wahrheit, welche als gute Probe dienen kann, wenn man die
Lineale in die gewünschte Stellung bringt. Ergänzt man in dieser Weise die
Parallelogramme OAEC und ODFB der ersten Figur 21 Taf. 14, so ist
der Beweis derselbe.
Auch der sogen. Polysecteur von Matton gehört zu dieser Gruppe von Apparaten- wir
beschränken uns hier nur auf die betreffenden Veröffentlichungen hinzuweisen: Polysecteur et Polysectrices par Louis-Pierre Matton
(Lyon 1878). Le Bisegment. Principe nouveau de Geometrie
curviligne par Louis-Pierre Matton (Lyon 1876). Quadrature de tous les polygones réguliers, depuis le triangle équilatérales,
jusqu'au polygone d'un nombre infini de côtés, par Louis-Pierre Matton
(Lyon 1877).
An die bisher betrachteten Apparate reihen sich nun die bekannten Parallellineale mit sich kreuzenden oder mit parallelen
Verbindungsgliedern und an diese die Perspectivlineale,
welche dazu dienen, Gerade nach unzugänglichen Fluchtpunkten zu ziehen, und die
nunmehr einer näheren Betrachtung unterzogen werden sollen.
Unter den Apparaten zum perspectivischen Zeichnen nehmen
die sogen. Fluchtpunktlineale, auch Perspectivlineale genannt, unser Interesse besonders in
Anspruch und zwar scheint uns als vorzüglich beachtenswerth das vom Maler Streckfuſs in Berlin sinnreich construirte und
einfachste derartige Instrument.Das Lineal wird in ganz vorzüglicher Ausführung von der Mechanischen
Werkstätte Eduard Preißinger in München
geliefert.
Das von Streckfuß erfundene
Perspectivlineal, welches zum Ziehen von Fluchtlinien nach unzugänglichen
Verschwindungspunkten dient und das besonders bei der Anfertigung von
architektonischen Perspectivzeichnungen in schräger Ansicht vorzügliche Dienste
leistet, beruht auf folgenden einfachen geometrischen Prinzipien:
1) Läſst man zwei im Punkte D (Fig. 17 Taf.
14) fest verbundene Winkelschenkel an zwei fixen Punkten B und C (z.B. an in ein Reiſsbrett
eingeschlagenen Stiften) gleiten, so beschreibt der Scheitel D einen Kreisbogen BDC; denn durch drei
gegebene Punkte kann man nur einen Kreis beschreiben
(hier den Kreis BDCF). In diesem Kreise ist der Winkel
BDC Peripheriewinkel auf dem Bogen CFB und, da sich beim Gleiten der Winkelschenkel an den
Stiften B und C weder der
Winkel BDC, noch der Bogen CFB ändert, so muſs – nach dem Satze: Peripheriewinkel auf gleichen Bögen
sind einander gleich – der Punkt D sich nothwendiger
Weise auf dem Kreise BDCF bewegen.
2) Verbindet man nun mit den ursprünglich betrachteten zwei
Winkelschenkeln noch einen dritten solchen Schenkel fest im Punkte D (vgl. Fig. 18 Taf. 14), so
schneidet dieser beim Gleiten der beiden ersten Schenkel an B und C den Kreis immer in ein- und demselben
Punkte F; denn die Winkel BDF und CDF sind Peripheriewinkel und bleiben
beim Gleiten der beiden Schenkel B und C immer dieselben; es muſs also Punkt F, da ja gleiche Peripheriewinkel auf gleichen Bögen
stehen und die Punkte B und C festliegen, auch immer an ein und derselben Stelle der Kreislinie sich
befinden.
Liegt der dritte Schenkel nach der entgegengesetzten Richtung, wie
DA in Fig. 19 Taf. 14, also
auſserhalb des Kreises, so geht natürlich dessen Verlängerung, beim Gleiten der beiden ersten Schenkel an B und C, immer durch einen und denselben Punkt
F des Kreisumfanges.
Ist nun, wie in Fig. 23 Taf. 14
angenommen, ein Gebäude in schräger Ansicht in Perspective zu setzen, und es fällt
z.B. der rechts liegende Fluchtpunkt Fr für die wagerechten Linien des Bauwerkes
über das Reiſsbrett hinaus, so denkt man sich durch Fr mit dem Mittelpunkte M auf dem Horizonte einen Kreis so gelegt, daſs
derselbe den Horizont in einem auf das Reiſsbrett und nahe an den Rand desselben
fallenden zweiten Punkt D schneidet. Hierauf bestimmt
man sich zwei weitere Punkte dieses Kreises B und C symmetrisch zum Horizonte so, daſs sie noch auf das
Reiſsbrett zu liegen kommen, indem man CE = BE als
mittlere geometrische Proportionale zu den bekannten Strecken DE und EFr berechnet.
Es sei beispielsweise die Entfernung vom Augpunkte A bis zum unzugänglichen Fluchtpunkte Fr = 300m und der Augpunkt A
liege vom Randpunkte R des Reiſsbrettes (natürlich im
Maſsstabe der Zeichnung gemessen) 200m entfernt,
so daſs also RFr =
100m ist. Man lege nun durch Fr, wie vorhin
angegeben, einen Kreis, etwa mit dem Durchmesser DFr = 120m, wodurch
DR = 20m wird.
Nimmt man nun z.B. DE = 18m (also EFr =
102m), so hat man: DE : CE = CE : EFr (oder auch: DE : BE = BE : EFr) also: 18 : CE = CE : 102 und daraus
C\,E=\sqrt{18\,\times\,102}=42^m,84=B\,E.
Fällt hierbei einer dieser Punkte, B
oder C, über das Brett hinaus, so muſs man DE oder etwa auch DFr
und DE entsprechend kleiner annehmen.
Die drei geradlinigen Arme des Perspectivlineals sind nun nach
Form und Gröſse vollständig gleich angefertigt; aber sie sind so zusammengestellt,
daſs das obere und das untere sich decken, das dazwischen liegende jedoch zu beiden
Seiten entgegengesetzt liegt. Zum Ziehen der Fluchtlinien nach dem unzugänglichen
Punkte wird immer das untere Lineal benutzt und zwar dessen innere, durch den
Mittelpunkt des kreisförmigen Linealanfanges gehende Kante,
In dem vorliegenden Falle wird man nun den Punkt D auf dem Horizonte markiren, dann in den Punkten B und C (auſsen an den
gedachten Kreis berührend) zwei Stifte einschlagen und die drei Lineale mittels des
demselben beigegebenen Schlüssels so feststellen, daſs das untere mit seiner inneren
Kante am Horizonte, die beiden oberen mit ihren äuſseren Kanten an den beiden
Stiften anliegen und der Schnittpunkt dieser drei Kanten über den Punkt D zu liegen kommt. Die rückwärtige Verlängerung der
inneren Kante des unteren Lineals geht dann, während die beiden oberen Lineale an
den zwei Stiften gleiten, immer durch den unzugänglichen Fluchtpunkt Fr und die Kante AD halbirt den Winkel BDC.
Der vorstehend betrachtete Fall gilt, wenn der Horizont nicht zu
weit aus der Mitte des Reiſsbrettes zu liegen kommt. Rückt jedoch der Horizont nahe
an den oberen oder unteren Rand des Brettes, so bestimmt man die Punkte B und C nicht mehr
symmetrisch zum Horizonte, sondern so, daſs sie sich eben wieder möglichst an den
Rändern des Brettes befinden, und schlägt die beiden oberen Lineale durch, so daſs
nicht deren äuſsere, sondern ihre inneren Kanten an den Stiften gleiten. Der
Schnittpunkt D der drei Winkelschenkel fällt dann mit
dem Mittelpunkte des kreisförmigen Linealanfanges zusammen und man hat durch den auf
dem Horizonte markirten Schnittpunkt D einen kleinen
Kreis vom Durchmesser des scheibenförmigen Linealanfanges zu verzeichnen, um die
drei Lineale mittels des Schlüssels richtig einstellen zu können (vgl. Fig. 24 Taf.
14).
Das vom Architekten K. W.
Ellersdorfer in München abgeänderte Schloſs des Streckfuß'schen Perspectivlineales gestattet die Benutzung zum Ziehen von
Fluchtlinien nach einem links liegenden unzugänglichen
Verschwindungspunkte F1, ohne daſs man das Lineal aus einander zu nehmen braucht, indem man dasselbe
einfach umkehrt, so daſs das für einen Fr oben befindliche Lineal jetzt nach unten zu liegen
kommt, wobei wieder dessen innere Kante zum Ziehen der Fluchtlinien benutzt wird.
Die Berechnungsweise der nöthigen Punkte, sowie das Einstellen der Linie bleiben
natürlich unverändert, ob nun der unzugängliche Fluchtpunkt links oder rechts vom
Augenpunkte gelegen ist.
Ein einfaches, gut brauchbares Fluchtpunktlineal hat
Prof. ThibaultVgl. Thibault: Linien-Perspective, deutsch von
Reindel, Direktor der Kunstschule zu
Nürnberg, 1834 S. 118 ff. in Paris (1798) erdacht und eingeführt-
derselbe bezeichnet es als ein Instrument, womit auf mechanische Weise in einem
Bilde, ohne dessen Grenzen zu überschreiten, zusammenlaufende Linien, deren
Verschwindungspunkt unzugänglich ist, gezogen werden können. Das Instrument ist nur
auf wagerechten Flächen anwendbar.
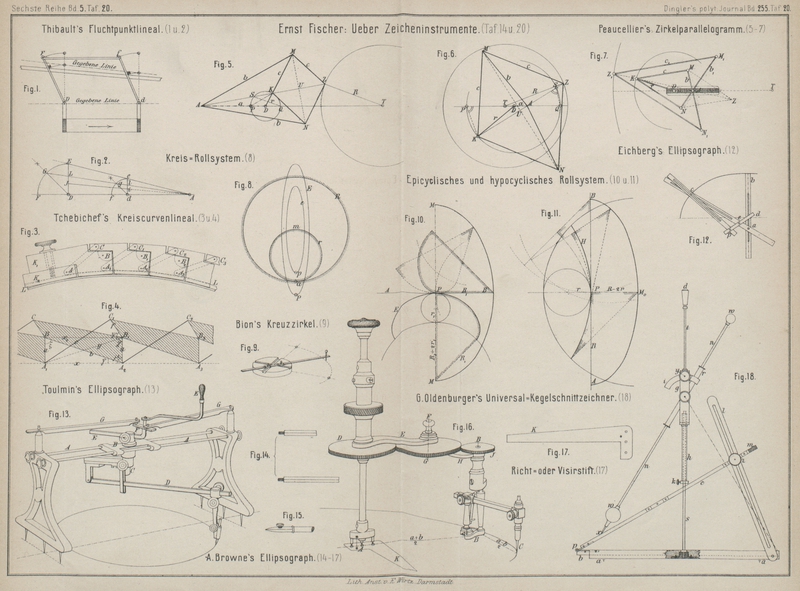
Fig. 2 Taf. 20
zeigt den geometrischen Satz, auf welchem dieses Instrument beruht. Man ersieht
daraus, daſs, wenn zwei Linien DE und de als die Bahn von zwei ähnlichen Dreiecken DEA und deA in zu einander proportionale
Theile getheilt werden, die Verbindungslinien – wie Ji
und Ll – sich auf die gemeinschaftliche Spitze A der Dreiecke hinziehen. Das Gleiche findet statt in
Bezug auf die zu einander ähnlichen Bögen FGE und fge.
Fig. 1 Taf. 20
stellt das Instrument im verjüngten Maſsstabe dar, mit dem an den beiden Seitenarmen
dergestalt angebrachten Lineale, und es erklärt sich hieraus die Art und Weise, wie
man damit Linien, welche in einem rechts liegenden Fluchtpunkte zusammenlaufen,
ziehen kann. Das vorliegende Instrument besteht also aus einem Parallelogramme DFdf, dessen bewegliche Seiten sich mittels an den
Ecken angebrachter Gelenke drehen; es ist zusammengesetzt aus einem Lineale, welches
zur Grundlage dient und an dessen Enden die beiden gleich langen Arme DF und df angebracht sind;
in einiger Entfernung von dem Lineale in den Punkten D
und d können sich die Arme ungehindert zusammenlegen.
Diese Arme sind unter sich durch einen Querarm Ff,
welcher an ihren oberen Enden durch zwei Gelenke verbunden ist, parallel
zusammengehalten. Mittels der vier Gelenke läſst sich das Instrument längs einer
geraden Linie ausstrecken. Jeder Seitenarm hat einen Falz oder eine Rinne mit
übergreifenden Rändern; dieselben sind bei dem einen Arme auf der äuſseren Seite,
bei dem anderen auf der inneren Seite angebracht und dienen zum Festhalten zweier
kleinen Schieber; diese letzteren sind aus drei Stücken zusammengesetzt: das erste,
im Falze oder in der Rinne befindlich und durch die überstehenden Ränder gehalten,
hat eine aus dem Falze hervorragende Schraube; das zweite Stück besitzt einen auf
den Rändern aufliegenden Querstift; dieser Stift ist ein Theil eines Cylinders mit
kreisförmiger Basis, auf seiner Achse von einem sehr kurzen Halbmesser
abgeschnitten, der nicht mehr als den vierten Theil des Kreises seiner Basis
enthalten soll; das dritte Stück ist eine Schraubenmutter, um den Stift auf dem Arme
anzudrücken und denselben an beliebiger Stelle zu befestigen. Diese Stifte dienen
zur Anlage eines beweglichen Lineales.
Da das Instrument sowohl auf der einen, als auch auf der anderen
Seite gebraucht werden soll, je nachdem die damit zu ziehenden Linien rechts oder
links zusammenlaufen, so müssen die Stifte der Schieber auf beiden Seiten über die
Dicke der Arme so viel hervorstehen, daſs sich noch das anzulegende Lineal, frei und
ohne anzustreifen, unter ihnen bewegen kann; ihre Achsen müssen gegen das Lineal
gewendet sein, welches sie beim Gebrauche immer berühren sollen.
Die Achsen der Gelenke, welche an dem feststehenden Theil der
Seitenarme angebracht sind, sollen von dem Lineale der Basis wenigstens um so viel
gleich weit entfernt sein, als die Breite des beweglichen Lineals beträgt, damit
dessen Rand, der zur Ziehung der verlangten Linien dient, sich leicht unter die
Achsen der Gelenke, welche immer auf eine der gegebenen Linien treffen sollen,
anlegen könne. Die Länge der beweglichen Theile der Seitenarme von der Achse der
Gelenke bis zum oberen Ende soll etwas weniger betragen, als ihre gegenseitige
Entfernung, damit, wenn sie sich beim Gebrauche zusammenlegen, derjenige Theil,
welcher sich innerhalb des Instrumentes befindet, ohne Hinderniſs die gegebene Linie
erreichen könne. Einer dieser Arme, derjenige, an welchem sich der Falz auſsen
befindet, soll auf dieser Seite einen Anhaltepunkt haben, damit der Arm sich nicht
weiter als bis zu einer Senkrechten zur Basis öffnen kann. Der Querarm muſs über die
Seitenarme etwas erhöht stehen, damit beim Gebrauche die Stifte der Schieber ihn
nicht aufhalten, sondern, ohne den Arm zu berühren, leicht unter dem letzteren
durchgehen; da der Querarm, wenn es nöthig ist, weggenommen und auf der anderen
Seite des Instrumentes angebracht werden soll, so müssen in demselben die
Mittelpunkte der Gelenke liegen.
Endlich sollen an den beiden Enden des Lineals der Basis
beiderseits gleich hohe schmale Vorsprünge etwas höher, als die Dicke des
beweglichen Lineals beträgt, angebracht sein, damit dieses unter den Armen, ohne zu
streifen, sich hin- und herbewegen kann. Diese Vorsprünge sind gezahnt und
verhindern das Ausrutschen des Lineals der Basis, wenn es auf einer gegebenen Linie
angelegt ist.
Das Instrument sammt dem beweglichen Lineale können aus hartem
trockenem Holze hergestellt werden, die Mittelstücke der Gewinde bezieh. Gelenke und
die Schieber aus Messing oder Stahl. – Wenn die Breite des Instrumentes zwischen den
Achsen der Gewinde 30cm beträgt, so kann damit ein
Lineal von ungefähr 150cm Länge angelegt
werden.
Thibault gibt an, es sei dem seinigen ein ähnliches
Instrument vorausgegangen; dasselbe sei in einem Werke abgebildet, welches von Lahure im J. 1790 zu Paris herausgegeben wurde.Das Thibault'sche Lineal ist auf Taf. 50 dieses
empfehlenswerthen Werkes in wahrer Gröſse abgebildet.
Thibault sagt: „Unser Instrument wurde zum ersten
Male im J. 1798 angefertigt; wir wollen zwar nicht auf den Vorrang Anspruch
erheben und, hätte das erste Instrument alle Vortheile erfüllt, welche wir
wünschten, so hätten wir nie an ein zweites gedacht.“
Nicholson zu London hat ein drittes derartiges
Instrument construirt; ein gewisser Castellan hat ein
viertes erfunden. Thibault bemerkt hierzu: „Es kommt
uns nicht zu, hier Lob oder Tadel über die verschiedenen dem unseren
vorangegangenen oder nachgefolgten Instrumente auszusprechen; diejenigen, welche
Gebrauch davon machen, sind allein im Stande, sie zu vergleichen und zu
würdigen; doch legen wir ihnen mit einem gewissen Vertrauen dieses hier vor,
nachdem wir seit langer Zeit dessen Nützlichkeit erkannt haben.“ – Hier
zeigt sich so recht der Werth der historischen Forschung auch auf dem von uns
betretenen Gebiete; denn würde man das Thibault'sche
Lineal einfach nachgeahmt haben, so besäſsen wir heute ein durchaus gutes
Fluchtpunktlineal; so aber verkehrt auf dem Markte ein Instrument, allerdings auf
demselben Prinzipe beruhend wie das Thibault'sche, aber
durch seine unzweckmäſsige Constructionsart mit solchen Fehlern behaftet, daſs es
Jedermann verwerfen wird, welcher es mit dem richtig construirten Thibault'schen Instrumente vergleichen kann.
Weniger elementar in ihrer Theorie als die bisher betrachteten einfachen Instrumente
sind die als Pantograph oder Storchschnabel bekannten EinrichtungenVgl. Ernst Fischer: Ueber Pantographen in Carl's Repertorium für
physikalische Technik, 1866 S. 258 ff. Mit 61 Figuren auf 6
Tafeln., welche uns in den Stand setzen, irgend eine gegebene
Figur in anderem Maſsstabe wiederzugeben. Von diesen Instrumenten kommen zwei
Hauptformen vor; die eine ist als der ältere
Storchschnabel, die andere als Mailändischer
Pantograph bekannt. Bei beiden ist eine Gelenkbewegung vorhanden, bei
welcher nur ein einziger Punkt absolut fest ist. Der Gelenkmechanismus ist so
eingerichtet, daſs zwei auf verschiedenen Armen liegende Punkte stets auf derselben
geraden Linie bleiben und ihre Abstände von diesem in einem bestimmten Verhältnisse
stehen. Hieraus folgt, daſs wenn man einen dieser beiden Punkte eine Figur umfahren
läſst, der andere eine ähnliche und ähnlich liegende Figur beschreiben wird, wobei
der Aehnlichkeitsmittelpunkt beider Figuren der feste Punkt ist. Bei dem älteren
Storchschnabel findet eine direkte, bei dem Mailändischen eine umgekehrte
Aehnlichkeit statt, d.h. im ersten Falle liegen die Figuren auf derselben Seite
ihrer Aehnlichkeitsmittelpunkte, im zweiten liegen sie auf entgegengesetzten Seiten.
In der vorhin angeführten Abhandlung über Pantographen haben wir nachgewiesen, daſs
der Pantograph schon vor 250 Jahren bekannt war und daſs ein Pater Christoph Scheiner als der Erfinder anzusehen ist. Scheiner hat eine ausführliche Beschreibung seiner
Erfindung nebst Andeutung der mannigfaltigsten Anwendung, welcher dieselbe fähig, in
seinem Werke: Pantographice seu ars delineandi (Rom
1631) niedergelegt. Auf dem Titelblatte zu diesem Werke deutet der Verfasser durch
eine höchst originelle Darstellung an, wie der Pantograph sogar an der Staffelei
benutzt werden könnte, um räumliche Gegenstände abzuzeichnen. Wir haben einige
Figuren aus dem Scheiner'schen Werke in unserer oben
angegebenen Abhandlung gebracht.
Die ersten Verbesserungen des Pantographen erwähnt Nils
Marelius, Premier-Lieutenant des kgl. schwedischen Landmesser-Comptoirs, in
seiner Schrift über den Storchschnabel, welche in den Abhandlungen der kgl.
schwedischen Akademie der Wissenschaften aus der Naturlehre, Haushaltungskunst und
Mechanik auf das J. 1766 abgedruckt ist. Auch Bion hat
in seiner mathematischen Werkschule schon im J. 1766 einen Pantographen abgebildet
und beschrieben. Wir haben 1866 in unserer angeführten Schrift sämmtliche bis dahin
bekannten Constructionen des Pantographen beschrieben und gute Zeichnungen davon
gegeben und verweisen daher im Uebrigen um so mehr auf dieselbe, als seitdem eine
wesentliche Aenderung in diesen Constructionen nicht vorgenommen worden ist.
In London 1876 bildeten die Pantographen, an deren Ausstellung sich auch Ott und Coradi in Kempten, Adrian Gavard in Paris und Oertling in London
betheiligt hatten, eine Abtheilung für sich. Bei der Mehrzahl dieser Pantographen
war die Verbindung zwischen dem festen Pole und dem Fahr- und Zeichenstifte in der
bekannten Weise durch ein Gelenkparallelogramm, in einzelnen Fällen jedoch durch
Rollen und Schnurlauf hergestellt. Das Bestreben der Verfertiger, möglichste
Leichtigkeit, Sicherheit und Genauigkeit der Führungen und der Berichtigung zu
erreichen, hat zu zum Theile sehr abweichenden Constructionen, welche man auch
bereits aus unserer genannten Abhandlung ersieht, geführt, wie z.B. bei Ott und Coradi, wo die Laufrollen dadurch ersetzt sind,
daſs der ganze Apparat mittels Metalldrähten an einem krahnartigen Gestelle frei
über der Zeichnung schwebt. Diese Idee ist übrigens bereits früher von Goldschmidt in Zürich praktisch ausgeführt worden.
Ueber die Instrumente zum Zeichnen der Kreisbögen von so
groſsen Radien, daſs die Mittelpunkte am Rande oder
selbst auſserhalb der Zeichnungsebene liegen, verdanken wir Prof. Helmert in Aachen höchst werthvolle Mittheilungen.Vgl. Helmert: Hilfsmittel zum Zeichnen sehr flacher
Kreisbögen in der Zeitschrift für
Vermessungswesen, 1877 S. 147 ff. Zum Vorzeichnen von
Kreisbögen nach groſsen Krümmungsradien bedient man sich des Stangenzirkels, der vorgearbeiteten Lehre,
der gebogenen SchieneVgl. Seyfert 1881
242 * 36. Ohnesorge
1882 246 * 366. Schönborn 1885 255 * 98.,
des Centrographen und der Zirkelparallelogramme.
Der Stangenzirkel, dessen wir schon weiter vorn kurz
Erwähnung gethan, gestattet nur eine beschränkte Anwendung und versagt für alle
Radienwerthe, welche einen gewissen Betrag überschreiten. Zudem erfordert seine
Anwendung einen beträchtlichen Raum auſserhalb des Umfanges der Zeichnung und es
gehört eine besondere Aufmerksamkeit dazu, nicht nur die Fehler wegen radialer
Schwankungen der Spitzen in Folge von Biegungen des Stabes zu vermeiden, sondern
überhaupt eine schöne und richtige Zeichnung zu erhalten.
Bequemer und zuverlässiger sind Lehren, welche in
Kartenpapier, Holz oder anderem passendem Materiale für bestimmte Radien bearbeitet
sind. Die Construction derselben erfolgt nöthigenfalls mittels zahlreicher aus
rechtwinkligen Coordinaten abgeleiteter Punkte. Ihrer allgemeinen Anwendung steht
aber der Umstand entgegen, daſs eben jeder Radius eine eigene Lehre erfordert,
wodurch auch nicht unerhebliche Kosten entstehen.
Eine gewissermaſsen veränderliche Lehre ist gewährt durch gebogene elastische Schienen. Kleine Theile einer solchen können ohne
weiteres als Kreisbögen angesehen werden. Längere Bögen erfordern jedoch zu ihrer
Herstellung einer besonderen Vorrichtung, welche der Schiene eine Kreisform
verleiht. Helmert hat im Literaturberichte der Zeitschrift für Vermessungswesen, 1875 S. 36 bereits
auf eine Abhandlung von H. Resal über einen Apparat zu kreisförmiger Biegung von Schienen bis 80°
Centriwinkel aufmerksam gemacht. Ein verwandtes, wohl noch sichereres Hilfsmittel
ist das Kreiscurvenlineal von Prof. Tchebichef, welches auf der Ausstellung in London 1876
vertreten war.
Aus Fig. 3 Taf. 20 ist zu
ersehen, daſs die Schiene L, welche eine kreisförmige
Biegung erhalten soll, an der Rückseite begrenzt und eingefügt ist in eine Kette von
mit einander zusammenhängenden gleichen Gliedern. Je zwei benachbarte Glieder sind
durch ein einfaches Gelenk B, B1
B2 u.s.w. verbunden;
auſserdem sind das erste und dritte, das zweite und vierte, das dritte und fünfte
Glied u.s.w. durch je ein das zwischenliegende Glied durchdringendes
Verbindungsstück, wie z.B. AC, verbunden. Die ersten
Glieder K1 und K2 können, wie die
Figur zeigt, durch eine Klemmschraube in einer bestimmten Stellung festgehalten
werden; in Wirklichkeit ist daselbst auch eine feine Bewegung, um mit aller Schärfe
K1 und K2 der Länge nach so
gegen einander verschieben zu können, daſs die gewünschte Krümmung eintritt.
Wenn nämlich eine solche Längsverschiebung vorgenommen wird, so
pflanzt sich dieselbe durch die Gelenke fort und, weil nur die äuſseren
Längsstrecken AA1, A1
A2, A2
A3... sowie CC1, C1
C2, C2
C3
... sich ändern können, dagegen die mittleren
Längsstrecken BB1, B1
B2, B2
B3... unveränderlich
sind, muſs eine Krümmung
der Gliederkette eintreten. An dieser nimmt die Schiene L Theil, weil sie durch passende einfache Vorrichtungen gezwungen ist,
sich dem von der Innenseite der Glieder gebildeten Polygon tangential
anzuschlieſsen.
Das in Fig. 3 Taf. 20 ungefähr in
⅓ n. Gr. (ohne strengen Anschluſs an die
Modellabmessungen) dargestellte Lineal gibt Krümmungen von r = ∞ bis r =4/3m. Um
sich eine Vorstellung von dem Betrage der zur Herstellung endlicher Werthe von r nöthigen Verkürzungen von A1
A2 zu bilden, kann man,
wie in Fig. 4
Taf. 20 BB1
= x0 und A1
A2
= x als zu gleichen Centriwinkeln gehörende Bögen von
Kreisen mit den Radien r und r
– a betrachten und hat dann r : r – a = x0 : x, woraus sich sofort findet: x0
– x = (a : r)x0. Für die Werthe a =
40/3mm und x0 = 3a = 40mm wird daher, entsprechend rmin = 4/3m, (x0 – x)max = 0,01. x0 = 0mm,4.
Unsere Aufgabe wird nun sein, nachzuweisen, daſs die Aenderungen von AA1,
A1
A2, A2
A3... durch geeignete Wahl der Abmessungen, ungefähr Fig. 3 und 4 entsprechend,
immer nothwendig gleich groß werden; dann wird auch die
Krümmung der Schiene L ihrer ganzen Länge nach in jedem
Falle demselben Radius angehören. Wir betrachten zu dem Zwecke die beiden stumpfen
Winkel CBA1 und C1
B1
A2, welche im
Anfangszustande bei gerade gestreckter Schiene einander gleich sein müssen und durch
Verkürzung von A1
A2 nicht merkbar
ungleich werden dürfen. Unter dieser Voraussetzung ist unschwer zu erkennen, daſs
eine durch Verschiebung von K1 gegen K2
entstehende Verkürzung von AA1 und die damit verbundene Aenderung des Winkels CBA1 alle folgenden entsprechenden Gröſsen
in gleicher Weise beeinfluſst. Eine kleine Ungleichheit dagegen wird proportional
der Anzahl der Glieder anwachsen und zwischen Anfang und Ende der Gliederkette eine
gröſste Abweichung der Winkel und Krümmungen hervorrufen. An dem in London
vorgelegenen Exemplare sollen die Winkelunterschiede weniger als 1/30° betragen;
doch ist nicht genau gesagt, welche Winkelunterschiede;
wahrscheinlich sind diese so, wie hier angenommen, zu verstehen.
Die Veränderungen des stumpfen Winkels CBA1 sind denjenigen des Winkels ζ bei B, negativ genommen,
gleich, wenn als Ursache der Veränderung eine Variabilität von A1
A2
= x auftritt. Wir drücken daher die Aenderung Δζ durch die Aenderung Δx
aus und, da Δx nicht ohne weiteres als Differential
angesehen werden darf, entwickeln wir Δζ als Function
von Δx nach dem Taylor'schen Satze unter Beibehaltung auch des quadratischen Gliedes. Ebenso
wird mit Δχ und Δψ, welche
die Veränderungen des Winkels C1
B1
A2 zusammen setzen,
verfahren.
Für den Anfangszustand
Fig. 4 Taf.
20, also für geradlinige Erstreckung der Schiene L, sei
der Einfachheit halber A1
B und A2
B1 senkrecht A1
A2 und BB1, also x = x0, μ = 90°. Auch sei Winkel A1
C1
B1 = 90°.
Zeichnet man die Werthe der Veränderlichen, wie schon für x geschehen, durch den Index Null aus, so ist ferner,
wenn noch x0 : a = n gesetzt wird:
x_0=a\,n.\ \ \ b=y_0=a\,\sqrt{1+n^2}\ \ \ \ \
\chi_0=\zeta_0.
sin\,\zeta_0=cos\,\gamma_0=n\,:\,\sqrt{1+n^2}.\ \
\ \ \ \ cos\,\zeta_0=sin\,\gamma_0=1\,:\,\sqrt{1+n^2}.
a\,b\,sin\,\zeta_0=b\,x_0\,sin\,\gamma_0=a^2\,n.\
\ \ \ c=y_0\,sin\,\psi_0.\ \ \ \ f=y_0\,cos\,\psi_0.
Man hat nun aus Dreieck A1
BA2 für x2
= a2 + b2 – 2ab cos ζ und hieraus folgt:
x=a\,b\,sin\,\zeta\,\frac{d\,\zeta}{d\,x} und
1=a\,b\,cos\,\zeta\,\left(\frac{d\,\zeta}{d\,x}\right)^2+a\,b\,sin\,\zeta\,\frac{d^2\,\zeta}{d\,x^2}.
Setzt man die Anfangswerthe ein, so ergibt sich:
\left(\frac{d\,\zeta}{d\,x}\right)_0=\frac{1}{a},
\left(\frac{d^2\,\zeta}{d\,x^2}\right)_0=\mbox{Null},
womit man nach Taylor's
Satz hat:
-\Delta\,\zeta=-\frac{\Delta\,x}{a}
(einschl. Glieder mit Δx2) . . . . . . . . . . (1)
Dasselbe Dreieck liefert noch die Gleichung a2
= b2
+ x2 – 2xb cos γ, woraus man wie vorher schlieſst:
0=x-b\,cos\,\gamma+x\,b\,sin\,\gamma\,\frac{d\,\gamma}{d\,x},
0=1+2\,b\,sin\,\gamma\,\frac{d\,\gamma}{d\,x}+x\,b\,cos\,\gamma\,\left(\frac{d\,\gamma}{d\,x}\left)^2+x\,b\,sin\,\gamma\,\frac{d^2\,\gamma}{d\,x^2};
\left(\frac{d\,\gamma}{d\,x}\right)_0=\mbox{Null}. \left(\frac{d^2\,\gamma}{d\,x^2}\right)_0=-\frac{1}{a^2\,n}.
Diese Differentialquotienten beziehen sich auch auf μ, da γ und μ nur um eine Constante unterschieden sind.
Das Dreieck A1
B1
A1 ergibt:
y^2=a^2+x^2-2\,a\,x\,cos\,\mu. y\,\frac{d\,y}{d\,x}=x-a\,cos\,\mu+a\,x\,sin\,\mu\,\frac{d\,\mu}{d\,x}.
\left(\frac{d\,y}{d\,x}\right)^2+y\,\frac{d^2\,y}{d\,x^2}=1+2\,a\,sin\,\mu\,\frac{d\,\mu}{d\,x}+a\,x\,cos\,\mu\,\left(\frac{d\,\mu}{d\,x}\right)^2+a\,x\,sin\,\mu\,\frac{d^2\,\mu}{d\,x^2}
\left(\frac{d\,y}{d\,x}\right)_0=\frac{n}{\sqrt{1+n^2}}. \left(\frac{d^2\,y}{d\,x^2}\right)_0=-\frac{n^2}{a\,\sqrt{1+n^2}}\,3.
Dasselbe Dreieck gibt noch:
x^2=a^2+y^2-2\,a\,y\,cos\,\chi. x=(y-a\,cos\,\chi)\,\frac{d\,y}{d\,x}+a\,ysin\,\chi\,\frac{d\,\chi}{d\,x}.
1=(y-a\,cos\,\chi)\,\frac{d^2\,y}{d\,x^2}+\right(\frac{d\,y}{d\,x}\right)^2+2\,a\,sin\,\chi\,\frac{d\,y}{d\,x}\,\frac{d\,\chi}{d\,x}+a\,y\,cos\,\chi\,\left(\frac{d\,\chi}{d\,x}\right)^2+a\,y\,cos\,\chi\,\frac{d^2\,\chi}{d\,x^2}.
\left(\frac{d\,\chi}{d\,x}\right)_0=\frac{1}{a\,(1+n)^2}. \left(\frac{d_2\,\chi}{d\,x^2}\right)_0=\frac{n\,(n^2-1)}{a^2(1+n^2)^2}.
\Delta\,\chi=\frac{\Delta\,x}{a\,(1+n^2)}+\frac{n\,(n^2-1)}{2\,(1+n^2)^2}\
\frac{\Delta\,x^2}{a^2} . . . . . . . . . . (2)
Das Dreieck A1
B1
C1 ergibt:
c^2=f^2+y^2-2\,f\,y\,cos\,\psi. 0=(y-f\,cos\,\psi)\,\frac{d\,y}{d\,x}+f\,y\,sin\,\psi\,\frac{d\,\psi}{d\,x}.
0=\left(\frac{d\,y}{d\,x}\right)^2+(y-f\,cos\,\psi)\,\frac{d^2\,y}{d\,x^2}+2\,f\,sin\,\psi\,\frac{d\,y}{d\,x}\
\frac{d\,\psi}{d\,x}+f\,y\,cos\,\psi\,\left(\frac{d\,\psi}{d\,x}^2+f\,y\,sin\,\psi\,\frac{d^2\,\psi}{d\,x^2}.
\left(\frac{d\,\psi}{d\,x}\right)_0=-\frac{n\,tg\,\psi_0}{a\,(1+n^2)}. \left(\frac{d^2\,\psi}{d\,x^2}\right)_0=\frac{n^2\,(tg^2\,\psi_0-1)}{a^2\,(1+n^2)^2\,tg\,\psi}.
\Delta\,\psi=-\frac{n\,tg\,\psi_0}{(1+n^2)}\
\frac{\Delta\,x}{a}+\frac{n^2\,(tg^2\,\psi_0-1)}{2\,(1+n^2)^2\,tg\,\psi_0}\
\frac{\Delta\,x^2}{a^2}.
Mit Rücksicht auf Gleichung (1) und (2) kann man nun auch
setzen:
\Delta\,\chi+\Delta\,\psi=\frac{n\,tg\,\psi_0-1}{1+n^2}\,(-\Delta\,\zeta)+\left(\frac{n\,(tg^2\,\psi_0-1)}{tg\,\psi_0}+n^2-1\right)\,\frac{n\,\Delta\,\zeta^2}{2\,(1+n^2)^2} .
. . . . . (3)
Wählt man tgΨ0 so, daſs der Coefficient von (–Δζ) = 1 wird, so sind dann die Winkeländerungen bis auf
Glieder erster Ordnung einschlieſslich einander gleich und es wird daher für sehr
schwache Krümmungen die genaue kreisförmige Gestalt vorhanden sein. Dazu gehört:
tg\,\psi_0=\frac{2+n^2}{n}. \Delta\,\chi+\Delta\psi=(-\Delta\,\zeta)+\frac{n}{2+n^2}\,\Delta\,\zeta^2
. . . . . . . . . . (4)
Nimmt man im Maximum Δx =
–0,01x0 und
setzt x0 = 3a, n = 3, so ist (–Δζ) = +
0,03, daher Δχ + ΔΨ =
(–Δζ) + 0,273 ×
0,0009, d. i. im Winkelmaſse = 0,000245 × 3438 = 0,84 Minuten.
Will man die Glieder zweiter Ordnung thunlichst berücksichtigen,
so muſs man Sorge tragen, daſs Δχ + ΔΨ auch für einen
mittleren Werth von Δζ = (–Δζ) wird, tgΨ0 erhält damit einen etwas anderen Werth als nach Gleichung (4); setzen
wir also tg\,\psi_0=\frac{2+n^2}{n}+r, so folgt als
Bedingungsgleichung für v aus Gleichung (3), wenn [Δζ] den besonderen in Rede stehenden Werth von Δζ bezeichnet:
[-\Delta\,\zeta]=[-\Delta\,\zeta]\,\left(1+\frac{n\,r}{1+n^2}\right)+\frac{n}{2+n^2}\,[\Delta\,\zeta]^2,
worin die Glieder von der Ordnung v und vΔζ, vernachlässigt sind. Es wird:
tg\,\psi_0=\frac{2+n^2}{n}+\frac{(1+n^2)}{2+n^2}\,[\Delta\,\zeta].
\Delta\,\chi+\Delta\,\psi=(-\Delta\,\zeta)\,\{1+\frac{n}{2+n^2}\,([\Delta\,\zeta]-\Delta\,\zeta)\}
. . . . . . . . . . (5)
Gleichheit der Winkel besteht im Falle der Annahme des
letzteren Werthes für tgΨ0 im Anfangszustande und für Δζ = [Δζ]. Dazwischen erreicht der Unterschied ein Maximum
und zwar, wie die Gleichung zeigt, bei Δζ = ½[Δζ]. Sie beträgt alsdann:
-\frac{n}{4\,(2+n^2)}\,[\Delta\,\zeta]^2.
Nimmt man Δζ gröſser als [Δζ], etwa xmal so groſs,
so wird der Winkelunterschied
=+\frac{n}{2+n^2}\,\varkappa\,(\varkappa-1)\,[\Delta\,\zeta]^2.
Beide Abweichungen werden entgegengesetzt gleich für:
x (x – 1) = ¼ bezieh. x = ½ (1 + √2) = 1,207 . .
. . . . . . . . (6)
Um [Δζ] zu erhalten, muſs man demnach
den Maximalwerth von Δζ mit 1,207 dividiren.
Im Falle der mehrfach angenommenen besonderen Zahlwerthe ist:
(-\Delta\,\zeta)\,max=+0,03.\ \ \ \ \
[-\Delta\,\zeta]=+\frac{0,03}{1,207}=+0,025.\ \ \ \
tg\,\psi_0=11/3-0,0226.
Maximalwinkel unterschied ist gleich – 0,000043 in arc
oder – 0,15 Minuten.
Gegenüber der Annahme (4) bietet daher die Annahme (5) mit (6)
bebedeutende Vortheile, denn der Unterschied benachbarter Winkel ist nur noch ⅙ des
ersten Werthes und so klein, daſs auch bei einem Dutzend Gliedern Anfangs- und
Endwinkel nur um nahezu 2 Minuten oder 1/30 Grad abweichen. Wenn es also praktisch möglich
ist, die Glieder in genügender Annäherung den mathematischen Bedingungen
entsprechend herzustellen, so erfüllt das Curvenlineal von Tchebichef überraschend gut seinen Zweck.
Schlieſslich stellen wir nochmals die von Helmert theils gewählten, theils der besten Construction entsprechend
berechneten Abmessungen zusammen:
x0 = 3a. b = 3,1623a. c = 3,0495a. f = 0,8368a. CB1 =
3,5252a.
ζ0 = χ0
=72°27',1. Ψ0 =
74°39',3.Formel 4 gibt: Ψ0 = 74°44',7, c = 3,0509a, f = 0,8320a und
die Vergleichung mit obigen Werthen läſst den hohen Genauigkeitsgrad
beurtheilen, mit welchem die Theile des Lineals bearbeitet werden müssen,
wenn sie genügen sollen.
Das zu South Kensington ausgestellte Exemplar war sauber in Holz
ausgeführt und schien dem Berichterstatter Prof. Helmert recht bequem in der Anwendung zu sein. Leider, bemerkt Helmert, war es nach Lage der Verhältnisse nicht
möglich, seinen Genauigkeitsgrad zu prüfen.
(Schluſs folgt.)